Frictional and Frictionless
Systems
Frictional Systems
Friction
When two objects in contact are forced to move on each other, the resistant force that occurs at the contact surface opposite the direction of movement is friction. Friction that exists before one of the objects starts to move is called static frictional force. Static friction is the amount of force necessary to start movement of an object in a static state. Kinetic friction (or dynamic friction) is the friction that exists during the movement of the object, and it is the amount of force that the object must overcome to continue moving. A typical friction graph is shown in Fig 4-1. Static friction is proportional to the force; as the force increases, the friction also increases. When the force comes to a critical point (f max), the static friction is overridden and the object starts to move. From this point on, resistance to movement of the object is called kinetic friction. Theoretically, kinetic friction has lower values than static friction.
Friction between solid objects can be rolling or sliding, depending on the type of movement. Because orthodontic tooth movement is a slow process, the wire and bracket relationship can exhibit both static and kinetic forms of sliding friction because the application of force starts a complex biomechanical relationship between the wire-bracket-ligature-tooth-periodontium system and the alveolar bone. Before we give this relationship any detailed consideration, it is necessary to understand friction.
When a book on a table is in a stable state, it applies a load or force (A) equal to its weight on the table (Fig 4-2a). The table conducts a force (N) on the book of the same magnitude and in the opposite direction. Force A is the result of many force vectors spread over the entire surface of the book; if the book is of a homogenous structure, these force vectors will spread out equally on the contact surface, so the resultant vector of these forces is located in the geometric center of the book. The same conditions are valid for the resultant force N.
If the book is pushed lightly from left to right (Fig 4-2b), because of the force acting on the book (P), the magnitude, direction, and point of application of the force N begin to change, and so does the book’s homogenous distribution. The cause of this is the roughness of the contact surface. Let’s assume for a moment that the contact surface is a frictionless and vacuumed environment. In this case, after starting movement with a minor force (P), the book would maintain its velocity and direction in accordance with Newton’s first law, and no changes in the magnitude, direction, or point of application of the N force would occur. However, in this example, there is a rough, interlocking contact surface between the table and the book that could be seen if examined under a microscope. When the book is pushed with horizontal force P, it does not start to move immediately because of the resistant force (ie, friction) resulting from the interaction between these two materials. This resistance (frictional force [f]) is equal to and opposite force P, creating a resultant force (R).
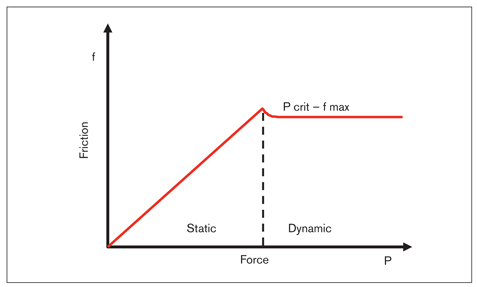
Fig 4-1 A typical friction graph. As the activating force (P) increases, the frictional force (f) also increases. The object starts to move as soon as the static frictional resistance is overridden. Dynamic (kinetic) friction, which is slightly less than static frictional force, starts from this point forward.1 (Reprinted from Niko-lai1 with permission.)
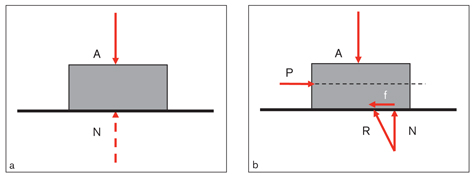
Fig 4-2 (a) When a book on a table is in a stable state, it applies a load (A) equal to its weight on the table. The table also applies equal and opposite force (N) on the book. (b) If a light horizontal force (P) is applied to the book from left to right, the book does not move immediately because of the static frictional force (f) between the book and the table. This force, which is tangent to the contact surface between the book and the table and opposite in direction, creates a resultant force (R).
If force P is increased up to the critical point, the frictional force f reaches the maximum level (f max). If force P exceeds the critical limit, the static frictional force will be overcome and the book will start to move. The book is now transferred from a static state to a dynamic state, and the frictional force f becomes dynamic (f dynamic) and decreases.
The values of f max and f dynamic depend on the magnitude of force A (the weight of the book in the example) and the coefficient of friction (μ) of the surfaces in contact (f = μ × A). This means that whether the object is in a static or dynamic state, the frictional force depends on the coefficient of friction of the surfaces in contact and the normal force between objects. In other words, the frictional resistance between the book and the table in this example depends on the weight of the book and the roughness of the surfaces. As the book’s normal force (weight) or the coefficient of friction increases, the friction also increases, and the force necessary to initiate the movement of the book (to overcome f max) also increases proportionally. Therefore, there is a direct proportion between force P and force f (ie, friction).
Theoretically, this equation is independent of the width of the contact surface. For example, when we push a box along the floor, the friction is always the same whether we stand the box vertically or horizontally. Whereas, if we push two boxes placed on top of one another, the amount of friction will be twice as much because the weight is double; however, a larger contact surface increases the possibility of interaction between the objects. Thus, even though friction in theory is independent of the objects’ contact surface, in practice the size of the contact surface is significant and must be considered.
The ratio between load A and friction (f) is constant (μ = f /A). This ratio is called the coefficient of static and kinetic (dynamic) friction, and it is shown as μs and μk, respectively. The coefficient of static friction is higher than that of kinetic friction, and it especially concerns orthodontists because a significant portion of the force applied to the tooth is spent overcoming the static frictional resistance between the wire, ligature, and bracket.
Analysis of the bracket-wire frictional relationship
Generally, friction is thought to occur only when a tooth slides along the archwire. Friction occurs, however, in all situations in which the wire is in contact with the bracket or ligature and in which there is a tendency for movement. For example, during leveling, a flexible archwire is placed in the brackets located at different levels and angulations to each other. The movement of teeth slides the wire through the bracket slots and tubes, resulting in friction between all the materials in contact: brackets, tubes, wire, and ligatures (Fig 4-3). Friction has an important impact on the efficiency of orthodontic mechanics because approximately 40% to 50% of the force used for tooth movement is lost to friction.2,3 Friction, or binding, which prevents the wire from sliding through the bracket slots, can delay and even halt tooth movement.
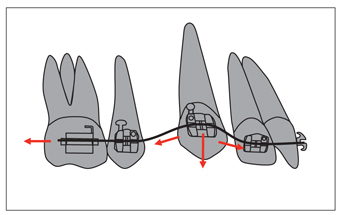
Fig 4-3 Friction exists during all movements in which the wire is in contact with the bracket and ligature. During leveling, when a flexible wire is placed in a high canine bracket, the tooth moves downward with the elasticity of the wire. As the curved wire is deactivated, it straightens by sliding through the adjacent brackets, with friction occurring between the wire, bracket, and ligature materials.2
For a better understanding of the bracket-wire relationship, let’s analyze the movements of a canine sliding along the archwire. Before distalization, a passive relationship exists between the canine bracket and the archwire (Fig 4-4a). When a constant, distal force is applied to the bracket, the tooth tips distally and the mesial wing of the bracket applies a downward force while the distal wing applies an upward force, creating a couple (clockwise moment, M1), as shown in Fig 4-4b. The deflected wire applies an opposite couple of equal magnitude to the wings of the bracket (counterclockwise moment, M2). The deflection of the wire is proportional to its stiffness in the load/deflection rate so that, for a given force, the deflection of stiff wires (such as stainless steel [SS]) is fairly low. As the angle (amount of tipping) between the wire and bracket slot increases, the friction also increases proportionally. When a certain point is reached, the wire resists and no more deflection occurs; thus, the tipping stops. The tooth starts to upright with M2 moment as the normal force is reduced. By overcoming the static frictional force, the tooth starts to move and slides along the straightened wire (Fig 4-4c).
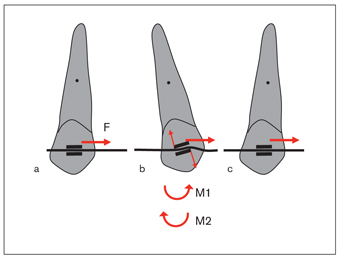
Fig 4-4 Stages of canine distalization with sliding mechanics. From the effect of force F (a), the tooth tips distally (M1) and touches the wire, then starts to upright from the counterclockwise moment (M2) applied by the wire to the bracket (b). When the static frictional resistance between the wire and bracket is overridden (c), the tooth starts to move distally by sliding along the wire. Canine distalization is achieved with multiple tipping-uprighting cycles like this one.
Excessive tooth tipping (high angulation between archwire and bracket) causes binding, and excessive distal force may lead to permanent deformation of the wire. Canine distalization along a wire is realized with tipping-uprighting cycles.3
In the transverse plane, as the force is applied from the buccal side of the canine’s center of resistance, the tooth rotates in a distopalatal direction (clockwise rotation; Fig 4-5). This effect is counteracted by an opposite couple from the ligature (counterclockwise rotation). During this distalization, several rotational and counterrotational movements occur.
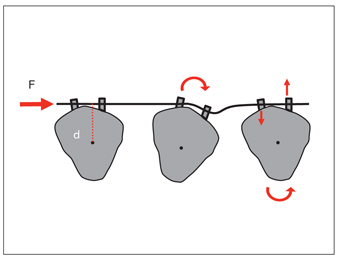
Fig 4-5 In the transverse dimension, distopalatal rotation occurs on the canine because of the force applied to the tooth. This rotational effect can be eliminated by the opposite couple of force that the bracket and ligature apply to the wire. During distalization, several rotational and counterrotational movements occur. d, perpendicular distance from the center of resistance to the line of action of the force (F).
The amount of tipping and rotation is inversely proportional to the stiffness of the wire. The tooth tips more easily on highly elastic wires; however, uprighting is much harder. On a stiff wire, the tooth tips slightly and uprights quickly. The clearance between the wire and bracket slot is also important for the amount of tipping. If the wire is stiff but its diameter is small, the amount of tipping will be that much more. During leveling, thinner wires cause less friction because they can slide easily through the bracket slots. However, in sliding mechanics such as canine distalization, SS wires (0.016-inch or 0.016 × 0.022–inch in 0.018-inch brackets) should be used to keep tipping and friction at an optimum level. In sliding mechanics, a minimum play of 0.002 inch in the bracket slot is necessary to minimize tipping and obtain effective sliding.
During canine distalization, friction occurs on at least six points between the wire, bracket, and ligature (Fig 4-6). Static or kinetic frictional forces can delay or stop tooth movement. Frictional forces are clinically unpredictable because friction is a multifactorial phenomenon. As friction delays tooth movement, the movement site becomes an anchorage site. If the frictional force is excessive, the posterior teeth start to move because the amount of force becomes an optimum force for anchorage teeth.
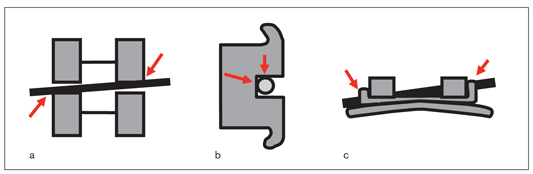
Fig 4-6 (a to c) During canine distalization, friction occurs on at least six points between the wire, bracket, and ligature.
Factors that affect friction between bracket and wire
Clinically, a number of factors may cause friction (Box 4-1), the amount of which varies depending not only on the magnitude of the force but also on the type of materials used and their surface characteristics. The amount of friction between smooth surfaces is obviously less than that between rough surfaces. However, several factors such as material, tightness of ligature, saliva, bracket width, and wire size can also affect friction. Because the consequences can directly affect the clinical outcome, this subject is examined in detail.
| Box 4-1 | Clinical factors that cause friction | |
| 1. Bracket | ||
| • Material2–8 | 4. Force | |
| • Width3,7, | ||
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


