Introduction
Mini-implants are now widely accepted as anchorage for orthodontic tooth movement because of the convenience of the placement procedure, their comparative low cost, and the fact that they can be immediately loaded after surgery. In this study, we incorporated a finite element approach and factorial analysis to determine the biomechanical effects of exposure length of the mini-implant, the insertion angle, and the direction of orthodontic force.
Methods
Twenty-seven finite element models were constructed to simulate the biomechanical response of the alveolar bone adjacent to the mini-implant. Factorial analysis was performed to investigate the comparative influence of each factor.
Results
The simulation results showed that the exposure length of the mini-implant had a statistically significant influence on bone stress, with a contribution of 82.35%. Increased exposure length resulted in higher bone stress adjacent to the mini-implant. Whereas all factors investigated had a statistically significant influence on cancellous bone stress, the stress values associated with cancellous bone were much less than those of cortical bone.
Conclusions
Increased exposure lengths resulted in higher bone stresses adjacent to the mini-implant. The percentage of contribution of the insertion angle of the mini-implant (6.03%) was also statistically significant but much less than that of the exposure length (82.35%). The direction of orthodontic force had no significant effect on cortical bone stress.
Anchorage during orthodontic treatment is a major challenge for dentists. Shapiro and Kokich proposed that endosseous implants can be used to provide anchors for tooth and bone movement. Compared with traditional anchorage reinforcements such as transpalatal arches and extraoral appliances, mini-implants are advantageous because of their smaller size, convenient insertion and removal procedures, relatively low cost, and the fact that immediate orthodontic loading is possible after surgery. However, a practical issue is mini-implant loosening, which can compromise the success rate of the procedure. The mini-implant failure rate for orthodontic anchorage is reportedly up to 30%.
Research studies have investigated biologic and mechanical factors, other than infection, that might be related to the failure of mini-implants. These factors include orthodontic force level, site of implantation, cortical bone thickness, and patient-dependent oral conditions. Although a mini-implant is used as a temporary anchorage device, its primary stability is crucial to the long-term success of the associated treatment. Because of limited interdental space, the mini-implant can be close to the root, and orthodontic forces can be transmitted directly to the alveolar bone via the mini-implant. Moreover, the development of a stress field incorporating the alveolar bone around the mini-implant is reportedly correlated with mini-implant failure.
Biomechanics is crucial in all aspects of dentistry, especially orthodontic treatment. After the application of an inappropriate external force to the oral environment, the development of a stress field in the supporting tissues is regarded as indicating an unsuccessful prognosis. Because of the increased availability, capacity, and usability of computer software in biologic modeling, finite element analysis has become a powerful tool for dental biomechanical research. Despite irregular geometry and uncertain loading conditions, finite element modeling can achieve a 3-dimensional representation of the internal or external structure; this is preferred over representations derived from exterior single-point measurements. Factorial analysis allows a sensitivity examination to consider all possible contributing factors and to determine which factors have the most influence in the biomechanical system. Once identified, the more influential factors can be further investigated, as can the interactions between them. The purpose of this study was to integrate a finite element approach and factorial analysis, to investigate the variables affecting bone stresses adjacent to alveolar bone.
Material and methods
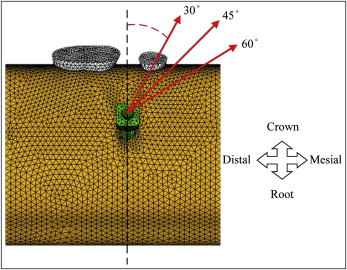
We used a commercial stainless steel mini-implant (A-1 C type implant system; Bio-Ray Biotech, New Taipei City, Taiwan) with a 2-mm diameter. For the purpose of the study, 3 lengths (8, 10, and 12 mm) were selected for model reconstruction. The geometry of the mandible, including both the second premolar and the first molar, was obtained from the Department of Dentistry of E-Da Hospital (Kaohsiung County, Taiwan), and computed tomography images captured at 3-mm intervals were digitized into digital imaging and communications in medicine (DICOM) format. Three-dimensional solid models of the mini-implant and the mandible were reconstructed and assembled by using commercial computer-aided design software (SolidWorks 2008; SolidWorks Corp, Waltham, Mass). The periodontal ligament was imitated at 0.25 mm in thickness and modeled based on the exterior geometry of both roots. The insertion of the mini-implant was assumed to be the middle point of both the premolar root in depth and the gap between the premolar and molar. Because the objective of this study was focused on bone stress, the crowns of both teeth were not incorporated to conserve calculation time. The entire model was imported to the finite element package (version 11.0; ANSYS, Canonsburg, Pa) and meshed by using 3-dimensional 10-node tetrahedral structural elements ( Fig 1 ). The bone, teeth, periodontal ligament, and mini-implant were all defined as homogeneous, isotropic, and linear elastic materials. The mechanical properties of the materials were based on published data and are listed in Table I . Before analysis, various element sizes were examined, ranging from 0.7 to 1.2 mm, to ensure convergence of the finite element model. Subsequently, 0.8 mm was determined as the appropriate element mesh size for all mesh models. The interfaces between teeth, periodontal ligament, bone, and mini-implant were all assumed to be bonded. Proximal and distal bone surfaces were fixed in all directions as the boundary conditions. The orthodontic force was 2 N (approximately 200 g), derived from previous reports and applied at the top surface of the mini-implant and inclined in the proximal direction. We aimed to simulate the en-masse retraction of anterior teeth. To this effect, we used a mini-implant with a 2.0-mm diameter. In addition, 2 N force is the maximum magnitude in the generally accepted range, according to the reported clinically safe limit for immediate loading.

| Material | Young’s modulus (MPa) | Poisson’s ratio | Reference |
|---|---|---|---|
| Mini-implant | 230000 | 0.3 | |
| Cortical bone | 14000 | 0.3 | |
| Cancellous bone | 300 | 0.3 | |
| Dentin | 18600 | 0.31 | |
| Periodontal membrane | 50 | 0.45 |
Statistical analysis
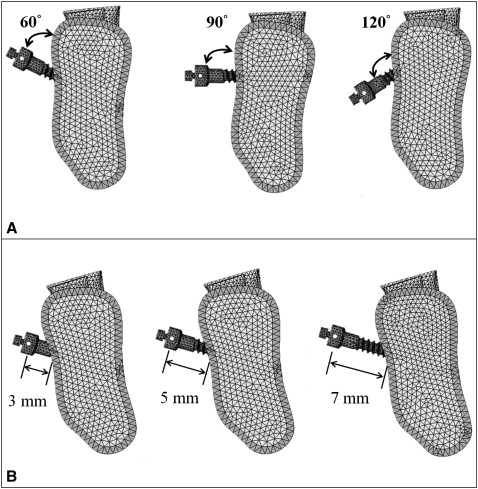
The factors affecting bone stress that were investigated included orthodontic force angle, insertion direction, and the exposure length of the mini-implant. In total, 27 mini-implant finite element models (3 orthodontic force angles with 3 insertion directions and 3 exposure lengths of the mini-implants) were analyzed ( Figs 2 and 3 ). The orthodontic force angle was defined as that between the line of applied force and the axis, which was parallel to the long axis of the tooth in the sagittal plane on the head of mini-implant. The insertion direction was determined based on the long axis of the mini-implant relative to the bone surface. Maximum von Mises stresses in cortical and cancellous bones were observed because of the viscoelastic characteristic of the bone. The main effect described the variation of the mean response of all factors based on the altered level for a specified factor. Correspondingly, the main effect plots and the contribution of each factor were generated by using a commercial statistical package (version 15.0; Minitab, State College, Pa). To determine the relative importance of these factors, a general linear model analysis of variance (ANOVA) test was performed, with P <0.05 deemed to indicate statistical significance.
Results
The maximum von Mises stress values of cortical and cancellous bones are listed in Table II . The ANOVA results of affecting factors and their interactions, generated to determine the relative importance of cortical and cancellous bones, are listed in Tables III and IV . The main-effect plots ( Figs 4 and 5 ) illustrate the variations in the maximum von Mises stresses at each level for each factor between cortical and cancellous bones.
| Model | Orthodontic force direction | Insertion angle | Exposure length (mm) | Cortical bone (MPa) | Cancellous bone (MPa) |
|---|---|---|---|---|---|
| 1 | 30° | 60° | 3 | 1.72 | 0.25 |
| 2 | 5 | 2.39 | 0.18 | ||
| 3 | 7 | 2.74 | 0.24 | ||
| 4 | 90° | 3 | 1.74 | 0.21 | |
| 5 | 5 | 2.18 | 0.15 | ||
| 6 | 7 | 3.32 | 0.19 | ||
| 7 | 120° | 3 | 1.53 | 0.08 | |
| 8 | 5 | 2.21 | 0.15 | ||
| 9 | 7 | 2.67 | 0.21 | ||
| 10 | 45° | 60° | 3 | 1.81 | 0.29 |
| 11 | 5 | 2.68 | 0.20 | ||
| 12 | 7 | 2.87 | 0.25 | ||
| 13 | 90° | 3 | 1.80 | 0.24 | |
| 14 | 5 | 2.11 | 0.16 | ||
| 15 | 7 | 3.51 | 0.20 | ||
| 16 | 120° | 3 | 1.52 | 0.08 | |
| 17 | 5 | 2.05 | 0.15 | ||
| 18 | 7 | 2.71 | 0.21 | ||
| 19 | 60° | 60° | 3 | 1.82 | 0.31 |
| 20 | 5 | 2.78 | 0.22 | ||
| 21 | 7 | 3.03 | 0.26 | ||
| 22 | 90° | 3 | 1.76 | 0.25 | |
| 23 | 5 | 1.92 | 0.16 | ||
| 24 | 7 | 3.39 | 0.20 | ||
| 25 | 120° | 3 | 1.45 | 0.08 | |
| 26 | 5 | 2.04 | 0.15 | ||
| 27 | 7 | 2.81 | 0.21 |
| Source | df | SS | MSS | %TSS | P |
|---|---|---|---|---|---|
| Force angle | 2 | 0.02 | 0.01 | 0.22 | 0.314 |
| Insertion angle | 2 | 0.58 | 0.29 | 6.03 | 0.000 ∗ |
| Exposure length | 2 | 7.91 | 3.95 | 82.35 | 0.000 ∗ |
| Force angle × insertion angle | 4 | 0.11 | 0.03 | 1.12 | 0.065 |
| Force angle × exposure length | 4 | 0.03 | 0.01 | 0.30 | 0.501 |
| Insertion angle × exposure length | 4 | 0.90 | 0.22 | 9.34 | 0.000 ∗ |
| Error | 8 | 0.06 | 0.01 | 0.65 | |
| Total | 26 | 9.60 |
| Source | df | SS | MSS | %TSS | P |
|---|---|---|---|---|---|
| Force angle | 2 | 0.0019 | 0.0009 | 2.04 | 0.000 ∗ |
| Insertion angle | 2 | 0.0430 | 0.0215 | 46.93 | 0.000 ∗ |
| Exposure length | 2 | 0.0114 | 0.0057 | 12.44 | 0.000 ∗ |
| Force angle × insertion angle | 4 | 0.0012 | 0.0003 | 1.36 | 0.005 ∗ |
| Force angle × exposure length | 4 | 0.0005 | 0.0001 | 0.51 | 0.074 |
| Insertion angle × exposure length | 4 | 0.0334 | 0.0083 | 36.41 | 0.000 ∗ |
| Error | 8 | 0.0003 | 0.0000 | 0.32 | |
| Total | 26 | 0.0917 |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


