In the previous article, I explained the meaning of the P value and discussed the danger of focusing the interpretation of the study results solely on P values. A better approach in presenting trial results is by reporting effect estimates (see the previous articles on effect estimates) and confidence intervals.
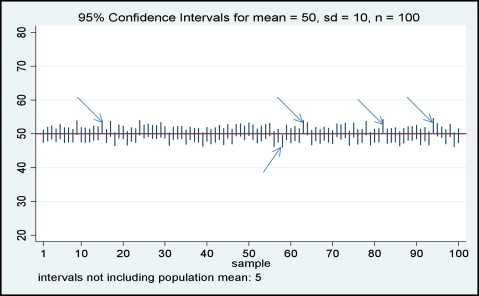
Confidence intervals show the range of the plausible differences of effect and the associations between the study groups, help us to determine whether the observed differences suggest true benefits and superiority of 1 treatment over the other, and offer valuable information for clinical decision making. But what is the confidence interval? If we draw 100 samples from the target population, 95% of the samples would contain the true population value ( Fig ). Confidence intervals always contain the effect point estimate and, depending on the confidence level, usually set at 95%, contain the true population value. The effect of an increased sample size on the P value is to decrease it, but the effect on the confidence interval is only to narrow its width around the same size of effect. The P value confines the interpretation of the trial results in the dichotomy of significant and nonsignificant, whereas confidence intervals move the interpretation of the results to the size of the effect and the association, and its range of plausible values given by the data under study. Confidence intervals shift the interpretation from a qualitative judgment to a quantitative estimate of the effect.
The CONSORT guidelines require that, for each outcome, study results should be reported as a summary of the outcome in each group (eg, mean, standard deviation, and proportion) together with the effect size (risk ratio or relative risk, odds ratio, risk difference, hazard ratio or difference in median survival time, and differences in means). Confidence intervals should be presented for the difference rather than separately for the outcome in each group.
The Table shows an example of reporting trial results from a randomized controlled trial comparing the time to alignment of the mandibular dentition with 2 types of nickel-titanium wires. We will use this Table to explain how the results should be interpreted. The data were analyzed by using time to event or survival analysis (Cox regression), and the effect estimate is presented as a hazard ratio, which is similar to the rate ratio. The hazard indicates the instant probability of an event occurring and the hazard ratio the instant probability of an event occurring in the nickel-titanium wires compared with the copper-nickel-titanium wires. The interpretation of the findings is as follows: the instant probability (hazard) of reaching alignment in the nickel-titanium group is 30% higher, or 1.3 times higher, than in the copper-nickel-titanium group. The associated confidence interval indicates that the instant probability of reaching alignment ranges from 30% lower to 150% higher in the nickel-titanium group compared with the copper-nickel-titanium group, and this is not a significant finding, since the value of 1 is included in the confidence interval.



