Introduction
Extraction of second permanent molars is an option for providing space in orthodontic treatment. Although many articles have described its impact on the outcome, there are few data on the prognosis of the eruption of the adjacent third molars. The aims of this investigation were to provide predictive models of eruption of third molars after second permanent molar extraction and to validate them.
Methods
A total of 48 patients (ages, 11-23 years) who had 128 second permanent molars (54 maxillary, 74 mandibular) extracted during orthodontic treatment were followed until eruption of the third molars was complete.
Results and Conclusions
A lineal regression model predicted the final angle of the third molars with the permanent first molar by using the variables of initial angle, jaw, and the developmental stage of the third molar. A logistic regression model predicted the probability of correct eruption by using the variables of initial angle, jaw, sex, age, and the developmental stage of the third molar.
Extraction of second molars has been recommended for treatment of several malocclusions. Among the advantages is that the extraction space is not visible and has little impact on the anterior profile. Moreover, eruption of the third molars seems to be facilitated by second molar extraction, thus avoiding the need of surgical extraction of the former.
However, there are few data on variables affecting the prognosis of third molar eruption after second molar extraction. It has been claimed that excessive tilting of the third molars, advanced development of their roots, and the patient’s age are important for success. Despite several predictive models of third molar eruption, there is no good predictive model on third molar eruption after second molar extraction until now. Such a model could be useful to calculate the probability of correct spontaneous eruption of a third molar after extracting the adjacent second molar.
Thus, our objectives in this study were (1) to make a lineal regression model to predict the final third molar tilting after extraction of the second permanent molar, by using data gathered before the extraction, and to validate this model; (2) to make a nonconditional binary regression model to predict whether the third molar will attain a correct final position after extraction of the second permanent molar, by using data gathered before the extraction, and to validate this model; and (3) to define the ideal conditions to extract a mandibular second permanent molar for orthodontic purposes to optimize the probability of correct eruption of the third molar.
Material and methods
A retrospective cohort of 48 patients who had finished orthodontic treatment involving second molar extractions and fixed appliances in both dental arches was consecutively selected. All were treated with the Ricketts or the straight-wire technique by the same orthodontist (C.D.-R.-G.) in a private practice in Manresa, Spain. The third molars were not included in the fixed appliance systeme. There were 19 male and 29 female patients, and 54 maxillary and 74 mandibular second molars were extracted. The patients ranged in age at the time of extraction from 11 to 23 years.
The inclusion criteria were (1) extraction of healthy maxillary or mandibular second molars previously or during orthodontic treatment and (2) presence of the third molar next to the extracted second molar. The exclusion criteria were (1) absence of other posterior permanent teeth in the arch in which the extractions were made and (2) lack of compliance with clinical follow-up visits after orthodontic treatment.
The patients were followed annually after orthodontic treatment. Sex, age at extraction of the second molars, and time of third molar eruption were obtained from the clinical records. Age was calculated in days, divided by 365.25 and computed with 2 decimals. Panoramic radiographs before the second molar extractions and after the eruption of the third molars were also obtained, and the following variables were identified: Nolla’s stage of development of the third molar at extraction of the adjacent second molar, and the angle between the third molar and the corresponding first molar just before the extraction of the second molar and after the third molar eruption (or in case of lack of eruption, after the third molar was considered to be impacted and with totally formed roots). All panoramic radiographs were made with the same equipment (Toshiba Panoura 1-C, Yoshida Dental, Tokyo, Japan). To determine third molar angulation, the first panoramic radiograph that showed full eruption was selected. Some patients had the final third molar angulation calculated from different radiographs.
The angles were calculated by drawing 2 lines on the panoramic radiograph of each subject: 1 perpendicular to the occlusal line that joined the cusps of the third molar and another line that joined the midpoint of the occlusal surface of the first molar with the midpoint between the 2 roots of the mandibular molars or the buccal roots of the maxillary molars. The angle was negative when the crowns converged or positive when they diverged. One third molar had its long axis in the buccolingual direction, which prevented drawing the line as described, and the angle was considered –90°. Figures 1 and 2 show how the angles were calculated.
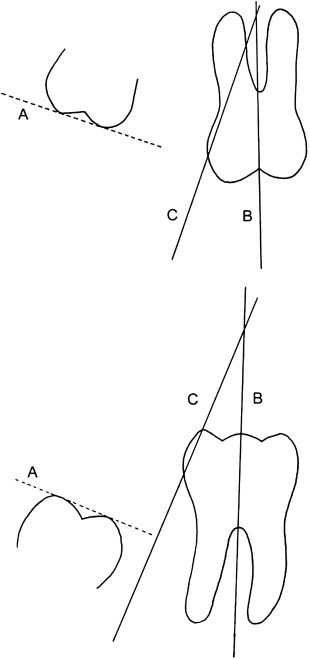
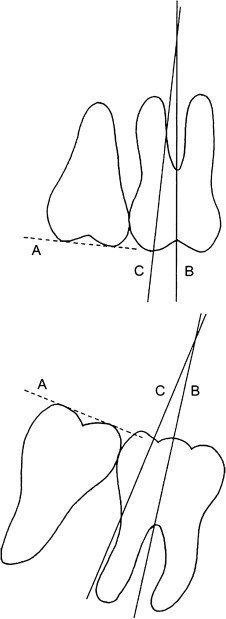
The final angle between the permanent third and first molars minus the initial angle between them was the uprighting of the third molar. A positive value indicated an increase of distal tilting, and a negative value, an increase of mesial tilting.
The third molar was considered “acceptably” erupted if it had erupted and had proximal contact with the adjacent first molar, and the final angle between these 2 molars was between –35° and 35°. Occlusion was not considered a criterion of success, because some third molars were level with the occlusal plane, but their antagonists did not erupt. All data were processed with the Statistical Package for the Social Sciences software (version 10.0, SPSS, Chicago, Ill).
All measurements were made by the first author. To evaluate the intraobserver agreement, 20 third molar angles were measured, and the third molars were classified according to Nolla’s stages in 1 session, and, 14 days later angles were measured and classified again. Intraobserver agreement was compared with an intraclass correlation coefficient (ICC). The correlation was very good for the angle (the lower limit of the 95% CI was 99%) and Nolla’s stage (the 95% CI of the ICC was between 87% and 98%).
A multiple lineal regression model to predict the final angle of the third molar with the adjacent first molar and a nonconditional binary logistic regression model were created with a randomly selected 60% of the sample (77 third molars). The independent variables initially included were site of the molar (maxilla or mandible), sex, age and Nolla’s stage at extraction of the second permanent molar, the angle between the third and the corresponding first molar before the second molar extraction and first-degree interactions (ie, interactions between 2 variables). The dependent variable was the final angle of the third molar with the adjacent first permanent molar for the lineal regression model and the successful eruption for the logistic regression model. Both models were constructed by adding all independent variables and first-degree interactions and deleting them stepwise if this deletion did not substantially reduce either the R 2 or the Nagelkerke’s R 2 , in order to obtain the least complex explanation for the observation (parsimonious model). Thus, the criteria to select the model was maximization of the corrected R 2 and the corrected Nagelkerke’s R 2 , respectively. The assumptions of the models were tested, and the models were validated by using the 51 third molars that were not used to build the model. The shrinkage (difference between corrected R 2 with the initially selected sample and the validation sample) of the model was calculated. The cutoff point of the logistic regression model was selected with a receiver operating characteristic curve, and sensibility and specificity were calculated.
Results
The 48 patients (29 female, 19 male) had 128 second molars extracted (54 maxillary, 74 mandibular).
All 54 maxillary third molars erupted, but 4 were considered failures only because of an open proximal contact; the success rate was 92.6%. Another 3 third molars did not reach occlusion because of lack of eruption of the antagonist.
There were 49 successfully erupted mandibular third molars (66.2%). Four mandibular teeth did not erupt (5.4%). Of the 21 erupted mandibular third molars with defective positions, 11 had proximal contacts but were tilted more than 35° mesially, and the remaining 10 had open proximal contacts. Of these 10 molars, only 2 had an excessive mesial tilt. Six of the 21 incorrectly erupted third molars did not reach occlusion with their antagonists.
The distribution means and standard deviations of the variables for the third molars are shown in Tables I and II . A more detailed bivariate analysis of patients with failed and successful eruption was published as a preliminary report.
| Successfully erupted (n = 50) | Unsuccessfully erupted (n = 4) | Total (n = 54) | |
|---|---|---|---|
| Age ∗ | 15.1 (2.6) | 22.2 (1.7) | 15.6 (3.1) |
| Angle before extraction (°) | 20.4 (14.6) | 1.8 (30.0) | 19.0 (16.5) |
| Angle after eruption (°) ∗ | 7.9 (8.2) | 15.3 (6.8) | 6.2 (10.1) |
| Uprighting (°) | –12.4 (14.6) | –17.0 (23.2) | –12.8 (15.1) |
| Nolla stage ∗ | 6.6 (1.1) | 9.5 (0.6) | 6.9 (1.3) |
| Time to erupt (y) ∗ | 4.4 (1.9) | 2.8 (0.3) | 4.3 (1.9) |
∗ Significant differences between successfully and unsuccessfully erupted molars (Mann-Whitney U test, P <0.05). These tests must be interpreted with caution, since there were few third molars in the unsuccessful eruption group.
| Successfully erupted (n = 49) | Unsuccessfully erupted (n = 25) | Total (n = 74) | |
|---|---|---|---|
| Age (y) ∗ | 14.5 (2.1) | 16.7 (2.6) | 15.3 (2.4) |
| Angle before extraction (°) | –36.4 (16.2) | –29.8 (16.0) | –34.2 (16.3) |
| Angle after eruption (°) ∗ | –21.1 (6.9) | –39.3 (13.7) | –27.3 (13.0) |
| Uprighting (°) ∗ | 15.3 (14.8) | –9.4 (14.5) | 6.9 (18.8) |
| Nolla stage ∗ | 6.2 (1.2) | 7.8 (1.4) | 6.8 (1.5) |
| Time to erupt (y) ∗ | 4.5 (1.9) | 3.3 (2.0) | 4.1 (2.0) |
∗ Significant differences between successfully and unsuccessfully erupted molars (Mann-Whitney U test, P <0.01).
The tilt of the third molar could be predicted with the final multiple lineal regression model:
final angle = − 3.532 + 29.692 × u − 3.269 × n + 0.091 × i
where final angle is the final angle in degrees between the major axis of the third molar and the first permanent molar when the third molar had attained its final position, u is a binary variable with values of 0 for mandibular third molars and 1 for maxillary third molars, n is the stage of the third molar just before the extraction of the adjacent second molar, and i is the angle in degrees between the major axis of the third molar and the first permanent molar just before the extraction. As defined previously for angle measurements, positive values mean distal tilt, and negative values indicate mesial tilt. For instance, for a hypothetical mandibular third molar at Nolla’s stage 5 with an initial mesial tilt of 40° with the mandibular first molar, after the second molar extraction, the model predicted that the final angle would be –3.532 + 29.692 × 0 – 3.269 × 5 + 0.091 × (–40) = –23.517°.
This model did not include any interactions, because they caused collinearity (high correlation between variables). Analysis of variance (ANOVA) of the model is described in Table III . The final corrected R 2 was 78.7%, so it predicted almost 79% of the observed variations. Coefficients are shown in Table IV . The shrinkage (general technique to improve an estimator and to regularize ill-posed inference problems) was low (8.3%), so the model also performed well in an independent sample.
| Sum of squares | df | Square mean | F | Significance | |
|---|---|---|---|---|---|
| Regression | 24624.37 | 3 | 8208.12 | 94.52 | P <0.001 |
| Residual | 6339.42 | 73 | 86.841 | ||
| Total | 30963.79 | 76 |
| β | SD | |
|---|---|---|
| Upper (u) | 29.692 | 4.428 |
| Nolla (n) | –3.269 | 0.820 |
| Initial angle (i) | 9.073 × 10 –2 | 0.068 |
| Constant | –3.532 | 6.050 |
The correct eruption of the third molar could be predicted with the final logistic regression model:
P ( success ) = 1 / [ 1 + exp ( − 9.016 – 7.438 × u − 1.565 × g + 0.057 × x i + 0.553 × a + 0.389 × n ) ]
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


