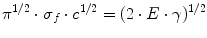(6.1)
where σ f is the tensile strength, γ, the specific surface energy and E, the modulus of elasticity.
The term on the right is independent of the size of the defect, contains only the material parameters and can be considered constant for a given material. Consequently, the term on the left is also a material constant and is called the fracture toughness, expressed by the symbol K IC .
For greater generality, the term π1/2 was replaced by a dimensionless factor Y, called the shape factor LEFM (linear-elastic fracture mechanics) (Eq. 6.3).
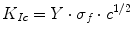
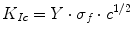
(6.3)
Equation 6.3 is known as the basic equation for linear-elastic fracture mechanics. The significance of this equation is that the characteristic fracture parameter of a material is not its tensile strength σ f , but the product of this term with the size of the crack defect c. That is, the mechanical strength of a material is limited by its greatest defect (the most critical in size, position or orientation). So this defect controls mechanical strength.
For tensions lower than the critical stress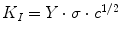 
, where K I is the stress intensity factor, the shape factor Y is a function of the size of the crack. For simplicity, a relative crack size X can be defined to relate crack size c with the dimension of component W.
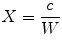
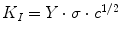, where K I is the stress intensity factor, the shape factor Y is a function of the size of the crack. For simplicity, a relative crack size X can be defined to relate crack size c with the dimension of component W.
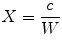
(6.4)
The function Y(X) can be calculated for many test geometries. For example, for a four point bending test, the following polynomial is a solution suggested in the literature Eq. 6.5):
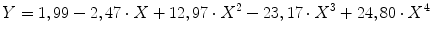
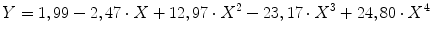
(6.5)
One can therefore say that the mechanical strength of a ceramic material is a combination of an invariable parameter dependent on the material––fracture toughness––and a variable parameter––the size of the limiting defect. The variation in resistance should be attributed to the variation in the size of the limiting defect (the defect that starts the catastrophic fracture).
When applied to fatigue and stress corrosion, Fracture Mechanics allows for the estimation of the performance of components, once the size of prior defects and/or nucleated cracks in service is known. It enables you to calculate the size of allowable defects and safe operating times.
The critical value for the stress intensity factor or fracture toughness (K IC ) is an intrinsic property of the material of the cracked component, for a given temperature situation, loading rate and microstructural condition. Because it is an intrinsic material property, the value of K IC can be used in the analysis of any geometry, permitting the calculation of the critical size of cracks in structural designs. This parameter also allows you to observe the influence of defect size on resistance.
Segui et al. (1995), as well as Sglavo and Pancheri (1997), report that K IC is a critical property that must be carefully evaluated in the selection of ceramic materials for dental use. There is, however, still a lack of research that correlates K IC and the clinical performance of dental ceramics.
In the past, the focus of fatigue research was restricted to damage and crack formation processes. Since the 1960’s, interest has shifted to the crack growth processes, due to the observation that:
(1)
crack growth through fatigue does not occur catastrophically (there is subcritical crack growth) and the cracks can even be immobilized in certain circumstances;
(2)
crack nucleation can occupy only a short period of fatigue life. The cracks are formed very early in the fatigue life of a material.
Data concerning crack growth in dental ceramics are very limited. According to Thompson (2004), Morena et al. (1986) were the first to estimate the parameters of slow crack growth in dental ceramics by determining flexural strength in an environment simulating the oral cavity. The authors assessed the influence of moisture on such materials, since water, under certain conditions, can degrade the properties of ceramic materials.
6.2 Tests for Determining K IC
According to Mukhopadhyay et al. (1999), there is no single, unambiguous method to determine the fracture toughness of ceramic materials, which explains the different approaches with different methodologies addressing the issue.
Several methods have been used to evaluate the subcritical crack growth of ceramics under static or cyclic loading conditions. A dynamic fatigue test, in which the flexural strength of specimens is measured as a function of the crosshead speed in a mechanical testing machine, is often used to determine the slow crack growth (SCG) parameters in the absence of cyclic load. Statistical methods based on experimental data for the initial strength and lifetime of specimens have also been successfully applied to evaluate the subcritical crack growth of ceramics under static or cyclic load. Weibull analysis is often used to statistically describe the strength of ceramics because it takes into account the typical asymmetric distribution of strength values of brittle materials.
Stay updated, free dental videos. Join our Telegram channel
VIDEdental - Online dental courses
