while the calculation formula of period prevalence is:
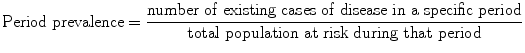
Prevalence is a proportion. It is dimensionless and can only take a numeric value in the range of zero to one (Table 7.1). Point prevalence is used to get a “snapshot” look at the population with regard to a disease. Period prevalence describes how much of a particular disease is present over a longer period that can be a week, month, or any other specified time interval.
Table 7.1
Comparison of measures of disease occurrence
|
Measure
|
Interpretation
|
Range
|
Unit
|
Cases
|
Source population
|
Uses
|
|---|---|---|---|---|---|---|
|
Prevalence
|
Probability
|
0–1
|
None
|
Existing
|
At risk of becoming a case
|
Planning
|
|
Incidence proportion
|
Probability
|
0–1
|
None
|
New
|
At risk of becoming a case
|
Etiologic studies
|
|
Incidence rate
|
Inverse of waiting time
|
0 to ¥
|
1/Time
|
New
|
At risk of becoming a case
|
Etiologic studies
|
Thus, a study group with an orthodontic treatment needing prevalence of 0.45 shows that 45 % of the subjects require some type of treatment at the time of the examination.
7.2.2 Incidence Proportion
Incidence proportion is defined as the proportion of a population that becomes diseased or experiences an event over a period of time [5].
The calculation formula of incidence proportion is:
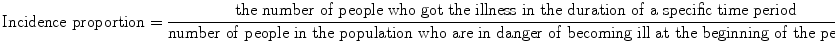
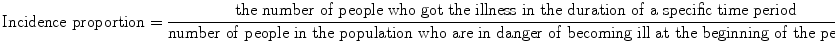
Incidence proportion is dimensionless and can only take numeric value in the range of zero to one (Table 7.1). Additionally, it is always referred to in the specific time period of being observed. Incidence proportion is also called cumulative incidence, average risk, or risk. Both the numerator and the denominator include only those individuals who, in the beginning of the time period, were free of illness and were thus susceptible to developing it. Therefore, cumulative incidence refers to those individuals who went from being “free of illness” at the beginning of the time period to being “sick” during that particular time period. Consequently, cumulative incidence can evaluate the average danger for individuals of the population to develop the illness during this time period. Cumulative incidence is mainly used for fixed populations when there are small or no losses to follow up. The length of time of monitoring observation directly influences the cumulative incidence: the longer the time period, the bigger the cumulative incidence. Thus, a 2-year incidence proportion of 0.20 indicates that an individual at risk has a 20 % chance of developing the outcome over 2 years.
A useful complementary measure to cumulative incidence is the survival proportion [5]. Survival is described as the proportion of a closed population at risk that does not become diseased within a given period of time and is the inverse of incidence proportion. Incidence and survival proportion are related using the following equation:
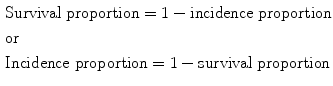
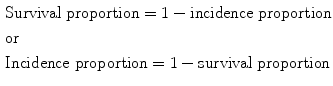
7.2.3 Incidence Rate
Incidence rate is defined as the relative rate at which new cases or outcomes develop in a population [3]. The mathematic formula of incidence rate is:


The sum of the time periods in the denominator is often measured in years and is referred to as “person-years,” “person-time,” or “time at risk.” For each individual of the population, the time at risk is the time during which this individual is found in danger of developing the outcome under investigation. These individual time periods are added up for all the individuals (Fig. 7.1).
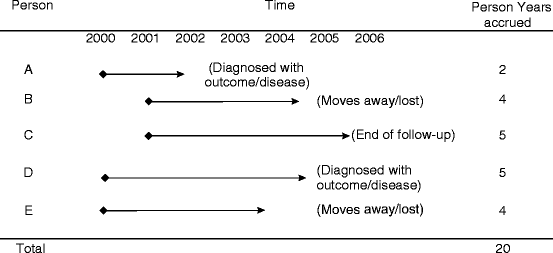

Fig. 7.1
Person-time measurement in a hypothetical population, individual follow-up times are known
Logic follows that the total number of individuals who change from being healthy to being sick, in the duration of each time period, is the product of three factors: the size of the population, the length of the time period, and the “strength of the unhealthiness” that acts upon the population. Dynamic incidence measures this specific strength of unhealthiness. The entry and exit of individuals from the population during the study period for reasons such as immigration, fatality from other causes, or any other competing risks are automatically taken into account. Therefore, including the time of danger in the definition, the incidence compensates for the main disadvantages that come into question from the calculation of the incidence proportion. The dynamic incidence is not a percentage, like the two previous indicators, since the numerator is the number of incidents and the denominator is the number of person-time units. The size of incidence rate is always bigger or equal to zero and can go to infinity (Table 7.1).
Thus, using the data presented in Fig. 7.1, we can estimate the following incidence rate: 2 cases/20 person-years = 0.1 cases/person-year, that indicates that for every 10 person-years of follow-up, 1 new case will develop.
7.2.4 Relationship Between Incidence and Prevalence
Among the indicators, various mathematic relations have been formulated, taking, however, certain acknowledgements into consideration [2, 3]. The equation that connects prevalence with incidence rate is:
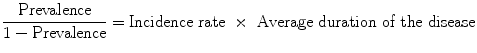
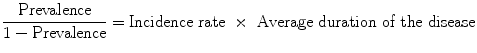
That is to say, prevalence depends on incidence as much as the duration of the illness. This is in effect when concerning a steady state, where the incidence of illness and the duration of illness remain constant with the passage of time. If the frequency of disease is rare, that is, less than 10 %, then the equation simplifies to:
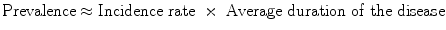
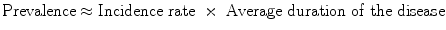
7.2.5 Measures of Causal Effects
A central point in epidemiologic research is the study of the cause of illnesses. For this reason, in epidemiologic studies, the frequency of becoming ill, among individuals that have a certain characteristic, is generally compared to the corresponding frequency among those that do not have this characteristic. The compared teams are often referred to as “exposed” and “not exposed.” Exposure refers to the explanatory variable, that is, any agent, host, or environment that could have an effect on health. The effect indicators are useful in order for us to determine if exposure to one factor becomes the cause of illness, to determine the relation between a factor and an illness, and to measure the effect of the exposure on the factor [3, 5, 6].
Comparing measures of disease occurrence in either absolute or relative terms is facilitated by organizing the data into a fourfold Table [7]. For example, the recorded data for the estimation of the prevalence and incidence proportion can be seen in Table 7.2.
Table 7.2
Organization of prevalence and incidence proportion data
|
Disease
|
||||
|---|---|---|---|---|
|
Exposure
|
Yes
|
No
|
Total
|
|
|
Yes
|
a
|
b
|
a + b
|
|
|
No
|
c
|
d
|
c + d
|
|
|
Total
|
a + c
|
b + d
|
a + b + c + d
|
|
While the presentation of facts for the estimation of the dynamic incidence can be seen in Table 7.3.
Table 7.3
Organization of incidence rate data
|
Disease
|
||||
|---|---|---|---|---|
|
Exposure
|
Yes
|
No
|
Person-time
|
|
|
Yes
|
a
|
–
|
Person-time exposed
|
|
|
No
|
c
|
–
|
Person-time unexposed
|
|
|
Total
|
a + c
|
–
|
Total person-time
|
|
7.2.6 Absolute Measures of Effect
Absolute effects are differences in prevalences, incidence proportions, or incidence rates, whereas relative effects involve ratios of these measures. The absolute comparisons are based on the difference of frequency of illness between the two teams, those exposed and not exposed [7]. This difference of frequency of illness between the exposed and not exposed individuals is called risk or rate difference, but also attributable risk or excess risk and is calculated using the following mathematical formula:
![$$ \mathrm{Absolute} ~ \mathrm{effect} = [\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{exposed}] - [\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{nonexposed}] $$](/wp-content/uploads/1008/A304574_1_En_7_Chapter_Equ0007h.gif)
![$$ \mathrm{Absolute} ~ \mathrm{effect} = [\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{exposed}] - [\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{nonexposed}] $$](/wp-content/uploads/1008/A304574_1_En_7_Chapter_Equ0007h.gif)
The difference measure gives us information on the absolute effect of exposure on the measure of disease occurrence, the difference in the risk to the exposed population, compared to those not exposed, and the public incidence of the exposure. The risk or rate difference has the same dimensions and units as the indicator which is used for its calculation (Table 7.4). The difference refers to the part of the illness in the exposed individuals that can be attributed to their exposure to the factor that is being examined, with the condition that the relation that was determined has an etiologic status. Thus, a positive difference indicates excess risk due to the exposure, whereas a negative difference indicates a protective effect of the exposure.
Table 7.4
Comparison of effect measures
|
Measure
|
Type
|
Range
|
Unit
|
Interpretation
|
|---|---|---|---|---|
|
Risk difference
|
Absolute
|
−1 to +1
|
None
|
Excess risk of disease among exposed population
|
|
Risk ratio
|
Relative
|
0 to +¥
|
None
|
Strength of relationship between exposure and disease, the number of times the risk of exposed subjects is higher or lower than the risk of nonexposed
|
|
Incidence rate difference
|
Absolute
|
−¥ to +¥
|
1/time
|
Excess rate of disease among exposed population
|
|
Incidence rate ratio
|
Relative
|
0 to +¥
|
None
|
Strength of relationship between exposure and disease, the number of times the rate of exposed subjects is higher or lower than the rate of nonexposed
|
7.2.7 Relative Measures of Effect
On the contrary, the relative measures of effect are based on the ratio of the measure of disease occurrence among exposed and not exposed [1]. This measure is generally called the risk ratio, rate ratio, relative risk, or relative rate. That is to say, the relative effect is the quotient of the measure of disease occurrence among exposed by the measure of disease occurrence among nonexposed.
![$$ \mathrm{Relative} ~ \mathrm{effect} = \frac{{\left[ {\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{exposed}} \right]}}{{\left[ {\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{nonexposed}} \right]}} $$](/wp-content/uploads/1008/A304574_1_En_7_Chapter_Equ0007i.gif)
![$$ \mathrm{Relative} ~ \mathrm{effect} = \frac{{\left[ {\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{exposed}} \right]}}{{\left[ {\mathrm{measure} ~ \mathrm{of} ~ \mathrm{disease} ~ \mathrm{occurrence} ~ \mathrm{among} ~ \mathrm{nonexposed}} \right]}} $$](/wp-content/uploads/1008/A304574_1_En_7_Chapter_Equ0007i.gif)
The relative comparisons are more suitable for scientific intentions [2, 3]. The relative risk gives us information on how many times higher or lower is the risk of somebody becoming ill. It also presents the strength of association and is used in the investigation of etiologic relations. The main reason is that the importance of difference in the measure of disease occurrence among two populations cannot be interpreted comprehensibly except in relation to a basic level of disease occurrence. The relative risk is a clean number.
If the risk ratio is equal to 1, the risk in exposed persons equals the risk in the nonexposed. If the risk ratio is greater than 1, there is evidence of a positive association, and the risk in exposed persons is greater than the risk in nonexposed persons. If the risk ratio is less than 1, there is evidence for a negative association and possibly protective effect; the risk in exposed persons is less than the risk in nonexposed. A relative risk of 2.0 indicates a doubling of risk among the exposed compared to the nonexposed. The power of the relative risk or relative rate can be accredited according to Table 7.5.
Table 7.5
Strength of association
|
Relative risk/rate
|
Relationship interpretation
|
|---|---|
|
1.1–1.3
|
Weak
|
|
1.4–1.7
|
Modest
|
|
1.8–3.0
|
Moderate
|
|
3.0–8.0
|
Strong
|
|
8.0–16
|
Very strong
|
|
16–40
|
Dramatic
|
|
40+
|
Overwhelming
|
We have examined the most commonly used measures in epidemiologic research that serve as tools to quantify exposure-disease relationships. The following section presents the different designs that can utilize these measures to formulate and test hypothesis.
7.3 Study Design
Epidemiologic studies can be characterized as measurement exercises undertaken to get estimates of epidemiologic measures. Simple study designs intend to estimate risk, whereas more complicated study designs intend to compare measures of disease occurrence and specify disease causality or preventive/therapeutic measures’ effectiveness. Epidemiologic studies can be divided into two categories: (a) descriptive and (b) etiologic or analytic studies [2, 7, 8].
7.3.1 Descriptive Studies
Descriptive studies have several roles in medical/dental research. They are used for the description of occurrence, distribution, and diachronic development of diseases. In other words, they are based on the study of the characteristics of individuals who are infected by some disease and the particularities of their time-place distribution.
Descriptive studies consist of two major groups: those involving individuals and those that deal with populations [7]. Studies that involve individual-level data are mainly cross–sectional studies. A cross-sectional study that estimates prevalence is called a prevalence study. Usually, exposure and outcome are ascertained at the same time, so that different exposure groups can be compared with respect to their disease prevalence or any other outcome of interest prevalence. Because associations are examined at one point in time, the temporal sequence is often impossible to work out. Another disadvantage is that in cross-sectional studies, cases with long duration of illness are overrepresented whereas cases with short duration of illness are underrepresented.
Studies where the unit of observation is a group of people rather than an individual are ecological studies. Because the data are measurements averaged over individuals, the degree of association between exposure and outcome might not correspond to individual-level associations.
Descriptive studies are often the first tentative approach to a new condition. Common problems with these studies include the absence of a clear, specific, and reproducible case definition and interpretation that oversteps the data. Descriptive studies are inexpensive and efficient to use. Trend analysis, health-care planning, and hypothesis generating are the main uses of descriptive design.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


