In certain situations, it is not possible to use patients as the randomization unit, so we must randomize to clusters (groups) consisting of a few, several, or many subjects who share some common characteristics. Clusters can be families, schools, communities, general practices, teeth in patients, or repeated measurements from the same participants over time. For example, in a trial involving oral health education delivered by the media, the unit of randomization might be entire towns, whereas randomizing persons would have been difficult and also inappropriate. In orthodontics, patients act in certain situations as clusters when they are contributing several teeth or when multiple measurements (repeated measures) over time are made on the same participants.

Cluster randomization differs in sample calculation and data analysis from individually randomized trials, which assume that observations are independent. In cluster-randomized trials, observations are correlated with less information obtained per subject and a consequent loss of power compared with individual randomized trials. In clustered trials, an increase in the sample size is required to compensate for the loss of information (loss of precision or power) because of this data correlation.

Imagine the following trial in which we want to evaluate the proportions of bond failures between 2 adhesives. In this scenario, a common option would be to randomize per patient, who will constitute a cluster; on average, each patient will contribute 20 teeth from premolar to premolar in nonextraction therapy. Some patients will receive adhesive A only, and some only adhesive B. Because the failures are not independent in patients, meaning that some patients will be more likely to break their appliances than others, the outcomes will tend to be correlated (clustered); therefore, the contribution of each tooth to the sample size is less than 1 because of the clustering effect (within-patient correlation of bond failures or no failures). Since the information contributed by each patient cluster is reduced, the required sample size must be increased by a factor related to the degree of correlation or the similarity of the outcomes within clusters.

Two parameters indicate the degree of correlation between subjects within clusters: the intracluster correlation coefficient (ICC or ρ [rho]) and the between-cluster coefficient of variation (k). Furthermore, there are sample-size formulas available for cluster randomized designs that use either the ICC or k. There will be more on this in part 2.

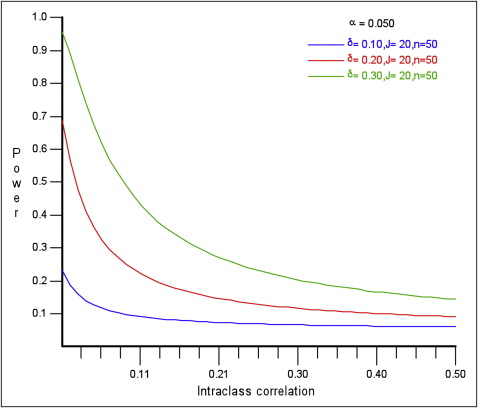
The ICC is 1 way to measure the degree of cluster variation and, like other correlation coefficients, can have a numeric value between −1 and +1. In practice, the values are usually positive, and a value of 0 means no clustering, whereas a value of +1 means that, within a cluster, the values are perfectly correlated. When the ICC = 0, each participant within a cluster contributes the same amount of information as he or she would have contributed to an individually randomized trial. However, when the ICC = 1, each cluster is considered as 1 individual. When the difference to be detected, the number of clusters, cluster sizes, and the significance levels remain constant, study power decreases as the ICC increases ( Fig ).

The graph shows how power decreases as the ICC increases for the various differences δ (0.10, 0.20, 0.30) between treatment groups, at alpha = 0.05 and for the same number of clusters (j = 20) and participants per clusters (n = 50).

The increased sample size required in cluster-randomized designs can be determined by the design effect, which is related to the ICC with the formula

Stay updated, free dental videos. Join our Telegram channel

Join