1 What is biomechanics?

Biomechanics is the research and analysis of the mechanical properties of living tissues and non-living objects that affect those living tissues. In orthodontics, this analysis of biomechanical properties is used to determine the effect of orthodontic appliances on oral tissues, particularly teeth and bone. The analysis of the non-living component simply follows Newtonian mechanical principles. In contrast, the biomechanical properties of living tissue are more complicated and often not thoroughly understood.^2,3

2 What is Newtonian mechanics?

Newton’s three Laws of Motion describe the relationship between the external forces acting on an object and the motion of that object, which form the basis for classical mechanics. Mechanics is the branch of physics concerned with the behavior of objects when subjected to forces or displacements. These laws were first formulated by Sir Isaac Newton and published in his work Philosophiae Naturalis Principia Mathematica (1687).^4,5

3 What are Newton’s three laws of motion?

4 What is force in physics?

In physics, force is an influence that may cause an object to change its velocity (accelerate). It may be experienced as a lift, a push, or a pull, and it has a magnitude and a direction and hence is mathematically represented by a vector. The actual acceleration of the body is determined by the vector sum of all forces acting on it. Forces can also cause deformation or rotations of an object.^6,7

5 What is a vector in physics?

A vector is a concept characterized by a magnitude and a direction. Force is a vector quantity defined as the rate of change of the momentum of the body that would be induced by that force acting alone. Since momentum is a vector, the force has a direction associated with it^6,7 (Fig. 8-1).

FIG 8-1 Force vector.

6 What is the difference between a vector and a scalar?

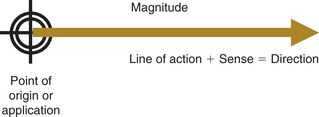
A vector is a concept characterized by a magnitude and a direction. A scalar has only a magnitude. An example of a vector is force and examples of scalars are weight and height. Orthodontic forces are described by their magnitude, point of application, and direction. The direction of the force is defined by the line of action and the sense (arrowhead). The magnitude of the force is depicted by the length of the line using an arbitrary scale (e.g., 1 cm represents 100 grams).^6,7

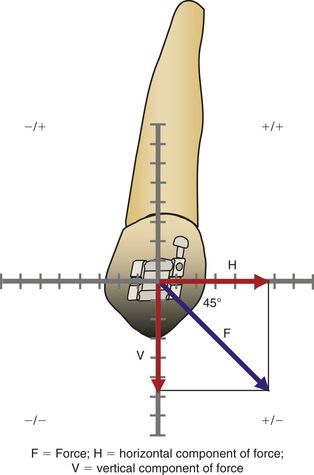
7 What are the horizontal and vertical components of an orthodontic force?

Any force applied to a tooth can be broken up into its vertical and horizontal components using the occlusal plane as the horizontal reference of an orthogonal coordinate system. The calculations of magnitude and direction of the components can be carried out geometrically as in Fig. 8-2 or by using trigonometric methods.⁸

FIG 8-2 Horizontal and vertical components of a force F applied to a tooth.

8 What is an orthodontic force system?

Delivery of physical force to the dentition is achieved by using a combination of force delivery methods. These include orthodontic wires, springs, elastic chains, and headgears. The force system describes all the forces involved and allows for analysis and calculation of resultant forces on a tooth or a group of teeth.²

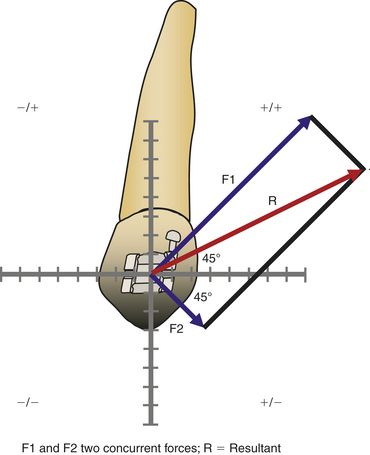
9 What are two methods to calculate the resultant of two concurrent forces?

Concurrent forces depicted as vectors can be added together to calculate the resultant by using the parallelogram method or by addition of their components in a reference system. For the latter method, the horizontal and vertical components of each of the two forces can be added to calculate the resultant as follows: If F₁ = h₁+v₁ and F₂ = h₂+v₂, then R = F₁+F₂ = (h₁+h₂) + (v₁+v₂).

The parallelogram method used to derive resultant forces entails drawing the two concurrent forces (F1 and F2 in Fig. 8-3) to scale at appropriate angulations. The ends of these lines are joined together with a parallelogram. The diagonal of this parallelogram from the point of force application, when measured and converted using the specified scale, gives the magnitude of the resultant (R). The direction of the resultant relative to any plane (e.g., the occlusal plane) can be determined using a protractor.^6,7

FIG 8-3 The resultant (R) for two concurrent forces F1 and F2 acting on a tooth.

10 What is the center of resistance (centroid)?

The center of resistance is analogous to the center of mass of a free body or its balance point. In physics, the center of mass of a sys/>