In the last 15 years, there has been an explosion of new technologies, instruments, and materials for nonsurgical and surgical endodontics. These developments have improved the precision with which endodontics is performed. The most important revolution has been the introduction and widespread adoption of the operating microscope (OM). Its introduction into dentistry, particularly in endodontics, has revolutionized how endodontics is practiced worldwide. This article provides basic information on how an OM is used in clinical endodontic practice and also gives an overview of its clinical and surgical applications.
Endodontists have frequently boasted that they can do much of their work blindfolded simply because there is “nothing to see.” The truth is that there is a great deal to see with the right tools.
In the last 15 years, for nonsurgical and surgical endodontics, there has been an explosion in the development of new technologies, instruments, and materials. These developments have improved the precision with which endodontics is performed. These advances have enabled clinicians to complete procedures that were once considered impossible or that could be performed only by talented or lucky clinicians. The most important revolution has been the introduction and widespread adoption of the operating microscope (OM).
OMs have been used for decades in other medical disciplines: ophthalmology, neurosurgery, reconstructive surgery, otorhinolaryngology, and vascular surgery. Its introduction into dentistry in the last 15 years, particularly in endodontics, has revolutionized how endodontics is practiced worldwide.
Until recently, endodontic therapy was performed using tactile sensitivity, and the only way to see inside the root canal system was to take a radiograph. Performing endodontic therapy entailed “working blind,” that is, most of the effort was taken using only tactile skills with minimum visual information available. Before the OM, the presence of a problem (a ledge, a perforation, a blockage, a broken instrument) was only “felt,” and the clinical management of the problem was never predictable and depended on happenstance. Most endodontic procedures occurred in a visual void, which placed a premium on the doctor’s tactile dexterity, mental imaging, and perseverance.
The OM has changed both nonsurgical and surgical endodontics. In nonsurgical endodontics, every challenge existing in the straight portion of the root canal system, even if located in the most apical part, can be easily seen and competently managed under the OM. In surgical endodontics, it is possible to carefully examine the apical segment of the root end and perform an apical resection of the root without an exaggerated bevel, thereby making class I cavity preparations along the longitudinal axis of the root easy to perform.
This article provides basic information on how an OM is used in clinical endodontic practice and an overview of its clinical and surgical applications.
On the relative size of things
It is difficult, even for a scientist, to have an intuitive understanding of size. Specifically, a dentist must have an accurate understanding of the relationship between the gross dimensions involved in restorative procedures and the dimensions of deleterious elements that cause restoration failure, such as bacteria, open margins, and imperfection in restorative materials. A filling or a crown may appear well placed, but if bacteria can leak through the junction between the tooth and the restorative material, then treatment is compromised.
A brief review of relative size may be helpful. Cell size is measured in microns (millionths of a meter, μm), and a single bacterial cell is about 1 μm in diameter. One cubic inch of bacteria can hold about a billion cells. A typical human (eukaryotic) cell is 25 μm in diameter, so an average cell can hold more than 10,000 bacteria. By comparison, viruses are so small that thousands can fit within a single bacterial cell. Simple calculations show that 1 in 3 can contain millions of billions of viruses.These calculations do not end there. For example, the size of macromolecules (eg, bacterial toxins) is measured in nanometers, or one-billionth of a meter ( Fig. 1 ).
Some of these bacterial toxins are so potent that even nanogram quantities can cause serious complications and even death. Clearly, dentists are at a severe disadvantage in their attempts to replace natural tooth structure with artificial materials that do not leak, in view of the virtually invisible microbiologic threats to restoration integrity.
The limits of human vision
Webster defines resolution as the ability of an optical system to make clear and distinguishable 2 separate entities. Although clinicians have routinely strived to create bacteria-free seals, the resolving power of the unaided human eye is only 0.2 mm. Most people who view 2 points closer than 0.2 mm will see only 1 point. For example, Fig. 2 shows an image of a dollar bill. The lines making up George Washington’s face are 0.2mm apart. If the bill is held close enough, one can probably just barely make out the separation between these lines. If they were any closer together, you would not be able to discern that they were separate lines. The square boxes behind Washington’s head are 0.1 mm apart and not discernible as separate boxes by most people. The boxes are beyond the resolving power of the unaided human eye. For the sake of comparison, it would take about 100 bacteria to span that square. Clinically, most dental practitioners will not be able to see an open margin smaller than 0.2 mm. The film thickness of most crown and bridge cements is 25 μm (0.025 mm), well beyond the resolving power of the naked eye.

Optical aids (eg, loupes, OMs, surgical headlamps, fiberoptic handpiece lights) can improve resolution by many orders of magnitude. For example, a common OM can raise the resolving limit from 0.2 mm to 0.006 mm (6 μm), a dramatic improvement. Fig. 3 shows the improvement in resolution obtained by the standard OM used in dentistry today. A clinical example is that at the highest power a restoration margin opening of only 0.006 mm is essentially sealed and this is beyond the common cement thickness film used in restorative dentistry.

The limits of human vision
Webster defines resolution as the ability of an optical system to make clear and distinguishable 2 separate entities. Although clinicians have routinely strived to create bacteria-free seals, the resolving power of the unaided human eye is only 0.2 mm. Most people who view 2 points closer than 0.2 mm will see only 1 point. For example, Fig. 2 shows an image of a dollar bill. The lines making up George Washington’s face are 0.2mm apart. If the bill is held close enough, one can probably just barely make out the separation between these lines. If they were any closer together, you would not be able to discern that they were separate lines. The square boxes behind Washington’s head are 0.1 mm apart and not discernible as separate boxes by most people. The boxes are beyond the resolving power of the unaided human eye. For the sake of comparison, it would take about 100 bacteria to span that square. Clinically, most dental practitioners will not be able to see an open margin smaller than 0.2 mm. The film thickness of most crown and bridge cements is 25 μm (0.025 mm), well beyond the resolving power of the naked eye.

Optical aids (eg, loupes, OMs, surgical headlamps, fiberoptic handpiece lights) can improve resolution by many orders of magnitude. For example, a common OM can raise the resolving limit from 0.2 mm to 0.006 mm (6 μm), a dramatic improvement. Fig. 3 shows the improvement in resolution obtained by the standard OM used in dentistry today. A clinical example is that at the highest power a restoration margin opening of only 0.006 mm is essentially sealed and this is beyond the common cement thickness film used in restorative dentistry.

Why enhanced vision is necessary in dentistry
Any device that enhances or improves a clinician’s resolving power is extremely beneficial in producing precision dentistry. Restorative dentists, periodontists, and endodontists routinely perform procedures requiring resolution well beyond the 0.2-mm limit of human sight. Crown margins, scaling procedures, incisions, root canal location, caries removal, furcation and perforation repair, postplacement or removal, and bone- and soft-tissue grafting procedures are only a few of the procedures that demand tolerances well beyond the 0.2-mm limit.
Optical principles
Because all clinicians must construct 3-dimensional structures in a patient’s mouth, stereopsis, or 3-dimensional perception, is critical to achieving precision dentistry. Dentists appreciate that the human mouth is a small space to operate in, especially considering the size of the available instruments (eg, burs, handpieces) and the comparatively large size of the operator’s hands. Attempts have been made to use the magnifying endoscopes used in artroscopic procedures, but these devices require viewing on a 2-dimensional (2D) monitor, and the limitations of working in 2D space are too restrictive to be useful.
Several elements are important for consideration in improving clinical visualization. Included are factors such as
-
Stereopsis
-
Magnification range
-
Depth of field
-
Resolving power
-
Working distance
-
Spherical and chromatic distortion (ie, aberration)
-
Ergonomics
-
Eyestrain
-
Head and neck fatigue
-
Cost.
Dentists can increase their resolving ability without using any supplemental device by simply moving closer to the object of observation. This movement is accomplished in dentistry by raising the patient up in the dental chair to be closer to the operator or by the operator bending down to be closer to the patient. This method is limited, however, by the eye’s ability to refocus at the diminished distance.
Most people cannot refocus at distances closer than 10 to 12 cm. Furthermore, as the eye-subject distance (ie, focal length) decreases, the eyes must converge, creating eyestrain. As one ages, the ability to focus at closer distances is compromised. This phenomenon is called presbyopia and is caused by the lens of the eye losing flexibility with age. The eye (lens) becomes unable to accommodate and produce clear images of near objects. The nearest point that the eye can accurately focus on exceeds ideal working distance.
As the focal distance decreases, depth of field decreases. Considering the problem of the uncomfortable proximity of the practitioner’s face to the patient, moving closer to the patient is not a satisfactory solution for increasing a clinician’s resolution. Alternatively, image size and resolving power can be increased by using lenses for magnification, with no need for the position of the object or the operator to change.
Loupes
Magnifying loupes were developed to address the problem of proximity, decreased depth of field, and eyestrain occasioned by moving closer to the subject. (Depth of field is the ability of the lens system to focus on objects that are near or far without having to change the loupe position. As magnification increases, depth of field decreases. Also, the smaller the field of view, the shallower the depth of field. For a loupe of magnification ×2, the depth of field is approximately 5 in [12.5 cm]; for a loupe of magnification ×3.25, it is 2 in [6 cm]; and for a loupe of magnification ×4.5, it is 1 in [2.5 cm].)
Loupes are classified by the optical method by which they produce magnification. There are 3 types of binocular magnifying loupes: (1) a diopter, flat-plane, single-lens loupe, (2) a surgical telescope with a Galilean system configuration (2-lens system), and (3) a surgical telescope with a Keplerian system configuration (prism-roof design that folds the path of light).
The diopter system relies on a simple magnifying lens. The degree of magnification is usually measured in diopters. One diopter (D) means that a ray of light that would be focused at infinity would now be focused at 1 meter (100 cm or 40 in). A lens with 2 D designation would focus light at 50 cm (19 in); a 5 D lens would focus light at 20 cm (8 in). Confusion occurs when a diopter single-lens magnifying system is described as 5 D. This designation does not mean ×5 power (ie, 5 times the image size). Rather, it signifies that the focusing distance between the eye and the object is 20 cm (<8 in), with an increased image size of approximate magnification ×2 (2 times actual size). The only advantage of the diopter system is that it is the most inexpensive system. But it is less desirable because the plastic lenses that it uses are not always optically correct. Furthermore, the increased image size depends on being closer to the viewed object, which can compromise posture and create stresses and abnormalities in the musculoskeletal system.
The surgical telescope of either the Galilean or the Keplerian design produces an enlarged viewing image with a multiple-lens system that is positioned at a working distance between 11 and 20 in (28–51 cm). The most used and suggested working distance is between 11 and 15 in (28–38 cm).
The Galilean system provides a magnification range from ×2 to ×4.5 and is a small, light, and compact system ( Fig. 4 ).

The prism loupes (Keplarian system) use refractive prisms and are actually telescopes with complicated light paths, which provide magnifications up to ×6 ( Fig. 5 ).
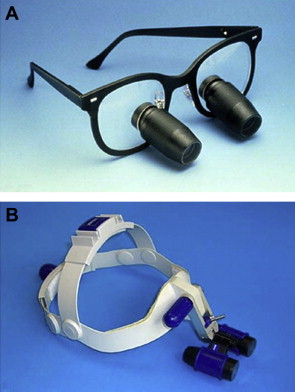
Both systems produce superior magnification and correct spherical and chromatic aberrations, have excellent depth of field, and are capable of increased focal length (30–45 cm), thereby reducing eyestrain and head and neck fatigue. These loupes offer significant advantages over simple magnification eyeglasses.
The disadvantage of loupes is that the practical maximum magnification is only about ×4.5. Loupes with higher magnification are available, but they are heavy and unwieldy, with a limited field of view. Using computerized techniques, some manufacturers can provide magnifications from ×2.5 to ×6 with an expanded field. Nevertheless, such loupes require a constrained physical posture and cannot be worn for long periods of time without producing significant head, neck, and back strain.
The problem of light
By increasing light levels, one can increase apparent resolution (the ability to distinguish 2 objects close to each other as separate and distinct). Light intensity is determined by the inverse square law, which states that the amount of light received from a source is inversely proportional to the square of the distance. For example, if the distance between the source of light and the subject is decreased by half, the amount of light at the subject increases 4 times. Based on the law, therefore, most standard dental operatory lights are too far away to provide the adequate light levels required for many dental procedures.
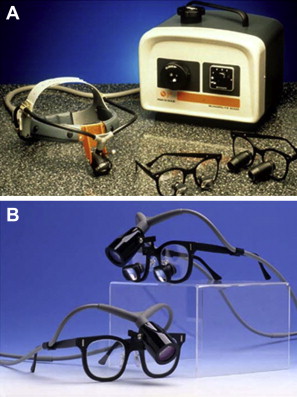
Surgical headlamps have a much shorter working distance (13 in or 35 cm) and use fiberoptic cables to transmit light, thereby reducing heat to minimal levels. Another advantage is that the fiberoptic cable is attached to the doctor’s headband so that any head movement moves the light accordingly. Surgical headlamps can increase light levels up to 4 times that of conventional dental lights ( Fig. 6 ).

Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


