Introduction
The aim of this study was to explore the shape differences in maxillary first molars with orthographic measurements using 3-dimensional virtual models to assess whether there is variability in morphology that could affect the alignment results when treated by straight-wire appliance systems.
Methods
A total of 175 maxillary first molars with 4 cusps were selected for classification. With 3-dimensional laser scanning and reconstruction software, virtual casts were constructed. After performing several linear and angular measurements on the virtual occlusal plane, the teeth were clustered into 2 groups by the method of partitioning around medoids. To visualize the 2 groups, occlusal polygons were constructed using the average data of these groups.
Results
The resultant 2 clusters showed statistically significant differences in the measurements describing the cusp locations and the buccal and lingual outlines. The rotation along the centers made the 2 cluster polygons look similar, but there was a difference in the direction of the midsagittal lines.
Conclusions
There was considerable variability in morphology according to 2 clusters in the population of this study. The occlusal polygons showed that the outlines of the 2 clusters were similar, but the midsagittal line directions and inner geometries were different. The difference between the morphologies of the 2 clusters could result in occlusal contact differences, which might be considered for better alignment of the maxillary posterior segment.
Highlights
- •
Maxillary first molar morphology varies according to 2 clusters.
- •
The clusters are differentiated by cusp location and buccal and lingual outlines.
- •
Cluster outlines are similar, but midsagittal line directions and inner geometries are different.
- •
Occlusal contact differences should be considered for better maxillary posterior alignment.
The straight-wire appliance (SWA), which is widely used in contemporary orthodontic treatment, was originally based on normative data of the dental arch form and individual tooth shape. With regard to tooth shape, the average crown angulation, inclination, and relative crown prominence values from nonorthodontic normal subjects were calculated and used as the guidelines for determining the built-in prescription of SWA systems. In this respect, research on the dimensions and the shapes of teeth should be considered as the fundamental basis for the orthodontic armamentarium.
Human dentition is not uniform but, rather, highly variable in its anatomic features. Teeth are by nature imperfect structures, often individually disfigured and collectively forming malocclusions. There have been several reports regarding tooth shapes and dimensions in the orthodontic literature, and orthodontists have traditionally focused on tooth dimensions, especially the mesiodistal dimensions, rather than shapes. However, dimensional aberrations directly affect good alignment, whereas peculiar shapes frequently need restorative procedures in which the dimensions can be modified at the same time.
Variations in the size, shape, and arrangement of teeth have been an area of great interest not only to orthodontists, but also to physical anthropologists. A number of studies have been carried out on interpopulational and interspecies differences to find evolutionary correlations between groups. For this purpose, diverse methods of odontometry have been widely used, and the use of 3-dimensional (3D) devices for odontometry has recently become popular. In addition, the developmental origins of tooth morphology are being elucidated with molecular biology.
The traditional measurements of tooth size, such as the mesiodistal and buccolingual diameters, are collective measures that do not provide sufficient information. In contrast, the introduction of the occlusal polygon with 3D technology gives more comprehensive information about tooth morphology. For example, the authors of a previous study investigated the shape of the mandibular molars with respect to their bracket positions and found 2 distinct groups according to the cusp and groove configurations.
The maxillary permanent first molar is the largest tooth in the maxillary dentition. Angle referred to this tooth as the “key to occlusion” because he thought that it was by far the most constant in taking its normal position. This hypothesis was the basis of Angle’s classification of malocclusions, which has withstood the test of time more than any of his other contributions and is still widely used as a universal description of malocclusions. Clinically, this tooth frequently is mesially rotated; this exacerbates the arch length discrepancy and Class II molar relationships.
According to the current version of the grading system for dental casts by the American Board of Orthodontics, the mesiodistal central grooves of the premolars and molars are used for the evaluation of proper alignment in the maxillary posterior region. Because of the tooth’s trapezoidal shape, SWA systems use general distal offset prescriptions of the tube or bracket. Although the maxillary first molars have shown less variability in their shape than the mandibular first molars, especially in their cusp numbers, there are some occasions when the universal use of 1 prescription does not meet the objective of acquiring optimal alignment or occlusion from clinical experience.
Until now, few studies have focused on the shape of the maxillary permanent first molar beyond its overall dimensions from an orthodontic perspective. In this study, we investigated the morphometric characteristics of maxillary permanent first molars using 3D technology and occlusal polygon methods. Our aim was to explore the shape differences in the maxillary first molars to assess whether there is considerable variability in morphology that affects the alignment results when treated with the SWA.
Material and methods
The study method used in this investigation has been previously reported. Two hundred Korean children (109 boys, 91 girls) at a minimum age of 10 years were selected from the data of the Korean Dental Growth Study. Informed consents were provided according to the Declaration of Helsinki, and the institutional review board for the protection of human subjects reviewed and approved the research protocol (S-D2010015).
The children were allowed to stay in the study if at least 1 maxillary molar was fully erupted, and also if the score of the simplified version of the tooth wear index was 0. Exclusion criteria of the investigation included any alterations on the teeth including caries, restorations, or surface defects that could affect measurements. Even if both maxillary first molars met the inclusion criteria, only 1 molar was randomly chosen, to rule out interdependence. Finally, a total of 175 maxillary first molars from 175 children (94 boys, 81 girls) were chosen for morphometric examinations.
The virtual 3D models were generated from the selected casts using a 3D scanner (optoTOP-HE; Breuckmann, Meersburg, Germany) according to the routine protocol previously reported. Then the prepared 3D models were analyzed, and measurements were made using specialized software (Rapidform 2004; INUS Technology, Seoul, Korea). The reference points were created through the consensus of 2 observers (H.-K.K. and Y.-S.P.); for reproducibility of the measurements, the process was repeated 2 times by the same 2 observers over a 3-week period. To test the reliability, 10 of the 3D scans were randomly selected and measured again on separate days 6 months after the initial measurements.
On the occlusal surfaces of the maxillary first molars, the following landmarks were identified to create reference points: 4 cusp tips (mesiobuccal, distobuccal, mesiolingual, and distolingual), 3 occlusal pits (central, mesial, and distal), and 2 contact points (mesial and distal). Based on these structures, the occlusal plane and the midsagittal line were defined for reproducible orientation and orthographic measurements ( Fig 1 ). The landmarks were identified with the customized program described in a previous study. After the occlusal plane was defined using the least squares method based on the locations of the 4 cusp tips, the normal vectors from all reference points mentioned above were drawn to add additional reference points for orthographic measurements. The midsagittal line was defined from the 3 additional reference points originally constructed from the mesial, central, and distal occlusal pits by the least squares method. The center of the midsagittal line was defined as C point by bisecting the line ( Table I ). In addition, 6 more occlusal reference points were created: the outermost points of the 2 grooves (buccal and lingual) and the 4 outermost points of each cusp (mesiobuccal, distobuccal, mesiolingual, and distolingual vertex) ( Fig 1 , C and D ).
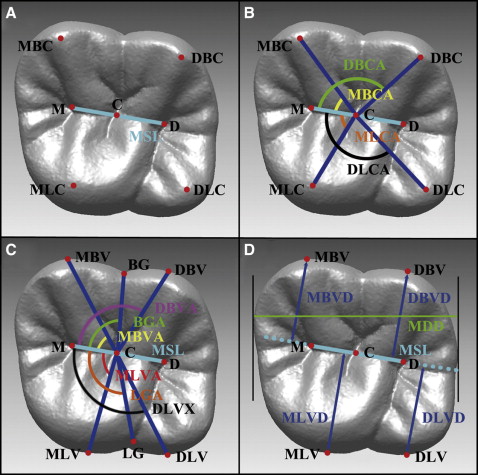
| Variable | Definition |
|---|---|
| Midsagittal line (MSL) | Virtual line constructed from 3 points (mesial pit, central pit, distal pit) by the least squares method |
| M | Mesial endpoint of MSL; foot of the mesial pit on the MSL |
| D | Distal end point of MSL; foot of the distal pit on the MSL |
| C | Center of MSL; the midpoint between points M and D |
| Mesiobuccal cusp angle (MBCA) | Angle formed by point M, point C, and the mesiobuccal cusp (MBC) tip |
| Distobuccal cusp angle (DBCA) | Angle formed by point M, point C, and the distobuccal cusp (DBC) tip |
| Mesiolingual cusp angle (MLCA) | Angle formed by point M, point C, and the mesiolingual cusp (MLC) tip |
| Distolingual cusp angle (DLCA) | Angle formed by point M, point C, and the distolingual cusp (DLC) tip |
| Buccal groove angle (BGA) | Angle formed by point M, point C, and the outermost point from the occlusal view on the mesiobuccal groove (BG) |
| Lingual groove angle (LGA) | Angle formed by point M, point C, and the outermost point from the occlusal view on the lingual groove (LG) |
| Mesiobuccal vertex angle (MBVA) | Angle formed by point M, point C, and the most prominent point of the mesiobuccal cusp of the teeth from the occlusal view (mesiobuccal vertex [MBV]) |
| Distobuccal vertex angle (DBVA) | Angle formed by point M, point C, and the most prominent point of the mesiobuccal cusp of the teeth from the occlusal view (MBV) |
| Mesiolingual vertex angle (MLVA) | Angle formed by point M, point C, and the most prominent point of the lingual side of the teeth from the occlusal view (mesiolingual vertex [MLV]) |
| Distolingual vertex angle (DLVA) | Angle formed by point M, point C, and the most prominent point of the lingual side of the teeth from the occlusal view (MLV) |
| Mesiobuccal vertex distance (MBVD) | Distance from MSL to MBV |
| Distobuccal vertex distance (DBVD) | Distance from MSL to distobuccal vertex (DBV) |
| Mesiolingual vertex distance (MLVD) | Distance from MSL to MBV |
| Distolingual vertex distance (DLVD) | Distance from MSL to distolingual vertex (DLV) |
| Mesiodistal diameter (MDD) | Distance between mesial contact point and distal contact point |
Additional parameters were constructed on the virtual casts to define the linear and angular characteristics of the maxillary first molar. First, the angles formed by the midsagittal line and the lines from the center to the respective 4 cusp tips were measured to determine the cusp tip locations. Next, the angles formed by the midsagittal line and the lines from the center to the respective 2 grooves and 4 vertices were also measured. For linear measurements, distances from the 4 cusp tips to the midsagittal line, distances from the 4 vertices from the midsagittal line, and also the mesiodistal diameter, which was defined as the distance between the mesial and distal contact points, were measured. The definitions of each measurement and descriptions are provided in Table I and Figure 1 , respectively.
Once the measurements described above were completed, principal component analysis was used to reduce the dimensionality. The cluster analysis was conducted using only 10 angular measurements to rule out the effect of size differences. Partitioning around medoids was used with the principal components. We tried to find 2 distinct clusters using the silhouette provided by partitioning around medoids, and then the molar samples were assigned to the classification table accordingly. Although the previously measured linear variables were not used in the classification of the morphotypes, this information was then added to describe the shapes of the maxillary first molars in more detail.
Statistical analysis
For the statistical analysis, the homoscedasticity and the normality of the measurement data were verified first. The Student t test was performed to examine any variables that could significantly influence the characteristic forms of the maxillary first molars. The reported P values were based on 2-sided levels of significance.
To visually examine the shape differences between the clusters, a polygon was constructed for each cluster according to the locations of the 4 cusp tips and the 4 vertex points. The resultant comparative diagrams were used to depict the morphologic differences between the clusters according to the unsupervised classification.
Results
The intraexaminer reliability coefficients ranged from 0.963 to 0.982. In terms of root mean squares, the random errors of estimation were lower than 0.06 mm for linear measurements and 0.57° for angular measurements. No variable showed a statistically significant difference between the test and retest measurements.
All maxillary first molars had 4 cusps. Because there were no statistically significant differences between the sexes in the comparison of angular measurements during the preliminary investigations ( Table II ), cluster analysis was performed on the pooled sample.
| Female (n = 81) | Male (n = 94) | |
|---|---|---|
| MBCA (°) | 45.44 ± 7.65 | 45.58 ± 7.96 |
| DBCA (°) | 118.20 ± 6.89 | 120.22 ± 5.46 |
| MLCA (°) | 76.10 ± 11.30 | 75.45 ± 10.68 |
| DLCA (°) | 145.34 ± 8.37 | 146.17 ± 7.64 |
| MBVA (°) | 72.13 ± 6.46 | 71.22 ± 8.26 |
| DBVA (°) | 105.67 ± 6.45 | 106.37 ± 7.37 |
| MLVA (°) | 89.39 ± 8.42 | 89.59 ± 8.28 |
| DLVA (°) | 124.95 ± 7.29 | 124.14 ± 8.76 |
| BGA (°) | 86.90 ± 6.17 | 87.24 ± 6.74 |
| LGA (°) | 110.36 ± 8.16 | 110.04 ± 10.24 |
| MBVD (mm) | 5.49 ± 0.45 | 5.50 ± 0.56 |
| DBVD (mm) | 5.38 ± 0.34 | 5.50 ± 0.40 |
| MLVD (mm) † | 5.64 ± 0.39 | 5.92 ± 0.40 |
| DLVD (mm) | 4.84 ± 0.51 | 4.95 ± 0.63 |
| MDD (mm) ∗ | 9.35 ± 0.68 | 10.27 ± 0.72 |
Using scree plots provided by the principal component analysis, 4 principal components were determined to account for about 87.2% of the sample variability of the data ( Tables III and IV ). We assumed that there were 2 clusters, since several measurements showed bimodal distributions in the exploratory data analysis. In addition, an average partitioning around medoids silhouette width was calculated to validate the number of clusters; a high average width represents good clustering. As a result, a cluster number of 2 showed the largest silhouette width in the trials of 2 to 20 clusters ( Fig 2 ). Therefore, 2 clusters appeared to be an appropriate number for grouping the pooled 175 maxillary first molars according to morphologic characteristics. Based on the results of clustering, 107 molars belonged to cluster 1, and the remaining 68 molars belonged to cluster 2.
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| MBCA | 0.562 | −0.252 | 0.052 | −0.420 |
| DBCA | −0.421 | 0.507 | 0.278 | −0.057 |
| MLCA | −0.085 | −0.131 | −0.425 | −0.086 |
| DLCA | 0.073 | −0.509 | 0.630 | 0.182 |
| MBVA | −0.077 | 0.058 | 0.167 | −0.442 |
| DBVA | 0.120 | −0.194 | −0.355 | 0.129 |
| MLVA | 0.419 | 0.434 | 0.043 | −0.448 |
| DLVA | 0.390 | 0.288 | 0.186 | 0.409 |
| BGA | 0.366 | 0.293 | 0.038 | 0.413 |
| LGA | −0.112 | −0.064 | 0.388 | −0.171 |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


