Introduction
The objective of this study was to assess the effects of age, sex, and the age-sex interaction on mean pain trajectories and individual variations in the pain experienced by adolescents after orthodontic separator placement.
Methods
We included 115 subjects (mean age, 14.99 years; SD, ±1.90 years; 56 boys, 48.7%; 59 girls, 51.3%) in this study. Orthodontic separators were placed in the mesial and distal contact points of the maxillary and mandibular first molars. A 100-mm visual analog scale was used for pain assessment at 11 prespecified times: 1 hour and 2, 4, 12, 24, 36, 48, 72, 96, 120, and 144 hours. A mixed-effects location scale model was used for the data analysis to directly model between-subject and within-subject variabilities in pain in addition to the usual modeling of mean pain as a function of age, sex, and time.
Results
Mean initial pain after 1 hour of separator placement for the 12- to 15-year-old male group was 13.52 mm on the visual analog scale, which initially increased rapidly (linear estimate, 9.16; P = 0.000; 95% confidence interval [CI], −8.65 to 9.67) but decelerated with time (quadratic estimate, −0.95; P = 0.000; 95% CI, −1.0 to −0.90), suggesting an inverted U-shaped mean pain trajectory. Age, sex, and age-sex interaction effects did not significantly influence initial pain. Compared with the 12- to 15-year-old male group, the 15- to 18-year-old female group reported the steepest rise in pain (estimate, 8.55; P = 0.00; 95% CI, 7.40 to 9.70) and, as a result, experienced the most overall pain. The 12- to 15-year-old male group reported minimum between-subjects variations (SD, ±4.6 mm) as well as within-subjects variations (SD, ±5.5 mm). The between-subjects variations were highest for the 12- to 15-year-old female group (SD, ±9.8 mm), whereas the within-subjects variations were highest for the 15- to 18-year-old female group (SD, ±10.1 mm).
Conclusions
The 12- to 15-year-old boys reported the lowest mean average pain intensity and a minimum subjective variation in between-subject and within-subject variances. The 15- to 18-year-old girls experienced maximum mean pain intensity and the highest daily fluctuations in pain intensity. The 12- to 15-year-old girls were the most different from one another in their overall pain experience.
Highlights
- •
We examined pain perception among adolescents after orthodontic separator placement.
- •
A novel “mixed-effects location scale model” was used to analyze pain trajectories.
- •
We explored mean scores and subject variability in pain as functions of age and sex.
- •
Subject variability included both between- and within-subject variations in pain.
- •
Age and sex have significant effects on mean scores and subject variability in pain.
Orthodontic force application during tooth movement induces complex biologic responses in and around the periodontium, resulting in the release of inflammatory mediators such as prostaglandin-E 2 , interleukin 1-beta (IL-1β), and substance P. These substances, which are essential for bone remodeling during tooth movement, also cause pain.
Pain is both patient- and time-dependent, resulting in substantial heterogeneity in patients’ reported pain trajectories over time. Put differently, pain is both a between-subject and a within-subject phenomenon. Evidence shows that most orthodontic patients report that pain commences during the first few hours after orthodontic force application, reaches peak intensity after 1 day, and eventually declines to almost pain-free levels after 7 days.
Bergius et al reported that the experience of pain varied substantially among subjects after elastic separator placement, suggesting between-subject variations in orthodontic pain perception. They further reported that the patient’s sex had a significant influence on orthodontic pain perception. A recent study highlighted the fact that patients’ age and sex have strong interaction as well as direct effects on orthodontic pain perception.
Describing pain trajectories would improve our understanding of how orthodontic pain conditions develop over time, and whether patients differ in pain perception. This understanding would then enable better management of orthodontic pain. In orthodontics, no study has ever been undertaken in this direction to understand pain trajectories. Importantly, previous studies have largely ignored between-subject and within-subject variations of pain and how these distinct sources of variation may depend on the patients’ characteristics. For example, do younger subjects tend to vary more in the overall average pain they experience (between-subject variation) than older subjects? Do female patients tend to report more fluctuating (ie, erratic or volatile) pain trajectories (within-subject variation) than male patients?
Mixed-effects models, also known as multilevel models and hierarchical linear models, can be used to analyze the evolution of subjects’ individual outcome trajectories over time; and to relate variations in these trajectories to subjects’ time-invariant characteristics such as age and sex of individual. Mixed-effects models can also incorporate time-varying subject characteristics to model occasion-to-occasion deflections or departures from subjects’ trajectories. Thus, mixed-effects models provide a popular way not only to estimate overall mean relationships, but also to quantify and then explain the degrees of between-subject and within-subject variations in patients’ outcomes over time.
Recently, Hedeker et al and Hedeker and Nordgren extended the standard 2-level random-intercept mixed-effects model to additionally model as a function of the covariates both the between-subjects variations in trajectories about their overall mean trajectory and the within-subjects variations in their observed measurements about their own trajectories. They called their model the “mixed-effects location scale model,” where “location” refers to the usual modeling of the mean response, and “scale” refers to the new direct modeling of the between-subjects and within-subjects response variability. They implemented their model in the stand-alone program MIXREGLS.
The objectives of this clinical research were to evaluate the overall mean orthodontic pain trajectory and the between-subjects and within-subjects variations about this over the week after orthodontic separator placement and to examine the influences of age, sex, and the age-sex interaction on the overall means, and the between-subjects and within-subjects variances using mixed-effects location scale models.
Material and methods
The sample size calculation was based on a power analysis concept used in a recent study in which the authors investigated the age-sex interaction effect on mean average orthodontic pain perception. Briefly, in this approach, which is based on the power analysis for a 2 × 2 factorial design, sample size is estimated for either of the binary coded groups (sex or dichotomized age) assuming that interest lies in detecting the same effect size for each binary group and then doubling the estimated sample size to detect the interaction effect.
The parameter estimates (including time function regression coefficients, and between-subjects and within-subjects variances, and so on) required for the power analysis were obtained from the authors of the previous study. Based on these parameters, the power analysis for the quadratic trend analysis was undertaken to determine the sample size, as recommended for the mixed-effect model for binary coded groups (eg, male and female). The standardized Cohen d effect size for a mixed-effects analysis is defined as d = slope coefficient/√ (between-subjects variance + within-subjects variance), where the slope coefficient may be for any polynomial function of time such as linear, quadratic, and so on.
Power analysis based on a study design with 1 baseline and 10 follow-up repeated measurements per subjects, an attrition rate of 10%, and a moderate effect size (Cohen d = 0.5) for the difference in slopes among the groups at a significance level of 0.05 and a power level of 0.80, showed that 60 participants (30 in each group) were required. Therefore, the total sample size required to detect the age-sex interaction effect on the mean response was 120 subjects (30 in each of the 4 groups).
The Cohen medium effect size for mean difference (d = 0.5) value corresponds to the Cohen medium effect size for correlation (r = 0.30), which can be used to find matching values for the regression coefficients in terms of 9% ( R 2 = 0.09) variance explained, which could be rounded to approximately 10%. Therefore, the sample size in this study was also calculated to be sufficient to detect a 10% difference in the variance among the groups.
The participants were consecutive patients who visited the private office of the first author (S.S.S.) for orthodontic treatment and were enrolled in the study if all inclusion criteria were satisfied, and informed consent was obtained. In total, 120 orthodontic patients were included in this study. The study protocol was approved (July 24, 2013) by the ethics committee of the Indian Medical Association, Jalandhar, Punjab, India.
The inclusion criteria were (1) 12- to 18-year-old adolescent boys and girls who required fixed orthodontic treatment, (2) erupted permanent first and second molars and no posterior open bite and interdental spaces, (3) no concurrent use of anti-inflammatory drugs, (4) caries-free dentition with a healthy periodontium, and (5) voluntary participation in the study confirmed by signing the informed consent form. The exclusion criteria were (1) a medical condition or systemic disease (eg, epilepsy, juvenile diabetes) that precluded the use of prospective fixed orthodontic appliances and (2) any chronic pain in the orofacial region or dental pain.
A previously established and standardized research model was used to assess orthodontic pain perception. In this model, orthodontic elastic separators are placed bilateral, mesial and distal to the first molars, in at least 1 jaw in adolescent patients (12- to 18-year-olds of both sexes), and then pain intensity is assessed over a 1-week period using a 100-mm visual analog scale (VAS).
In our study, orthodontic elastic separators (3M Unitek, Monrovia, Calif) were placed in the mesial and distal contact points of both maxillary and mandibular first molars. For all participants, separators were placed in the evening, between 5:00 and 7:00 pm , although on different days. This was done to ensure that for all participants, pain assessment time would be the same to minimize the influence of natural diurnal variations in pain intensities. On the day of separator placement, booklets with the pain assessment scale and written instructions were provided to the participants.
Pain was assessed with a VAS, which is a 100-mm-long horizontal line where one end corresponds to “no pain” and the other end indicates “worst pain possible.” This is a valid and reliable scale for pain assessment. To better understand the orthodontic pain trajectories, especially the within-subject variance component, we decided to increase the number of pain assessment occasions compared with the previously established model. In our study, the number of times for pain assessment was 11, which was more than double the 5 pain assessment occasions used previously. Pain was assessed at the following times after orthodontic separator placement: 1 hour and 2, 4, 12, 24, 36, 48, 72, 96, 120, and 144 hours.
To alleviate any confusion regarding the actual time of pain assessment, we reported pain assessment time in hours instead of morning or evening time of day. Because we inserted the orthodontic separators in the evening, the day 1 morning would correspond to 12 hours for pain assessment, in contrast to the usual notion in the orthodontic literature, where it is assumed that day 1 morning represents a 24-hour time period for pain assessment.
A trained research assistant, who was blinded to study, was responsible for data collection. The VAS scores in millimeters were measured from the left margin of the scale to the nearest millimeter with a metal ruler. To examine the reproducibility and reliability of the score measurements, 30 randomly selected VAS scores were measured by the first author independently. An intraclass correlation coefficient (ICC) of 0.93 showed excellent reproducibility and reliability.
The participants were also asked to record their analgesic consumption at each time point. No specific analgesic was prescribed, and the participants were free to use over-the-counter analgesics of their choice. Since no restrictions were applied in terms of dose, frequency, or type of analgesic, analgesic consumption data will be used only for descriptive purposes and will not be included in the analysis.
Statistical analysis
Orthodontic pain trajectories were estimated using 2-level random-intercept mixed-effects location scale models, treating the repeated measurements at level 1 nested within subjects at level 2. The models consisted of 3 separate equations for simultaneous modeling of the mean response, the log of the between-subjects variance, and the log of the within-subjects variance each as a function of the covariates. The detailed description of each equation is provided in the Supplementary Material . The log-link was used to ensure positive between-subject and within-subject variances. All models were fitted using the MIXREGLS program, calling it from within Stata software (version 13; StataCorp, College Station, Tex) using the “runmixregls” command. A complete technical description of the mixed-effects location scale model and its adaptation to our orthodontic pain study, as well as the details of the model fit/run-in, are described in the Supplementary Material .
Results
Of the 120 patients included in this study, 3 did not return the questionnaire, and 2 did not report back. The remaining 115 patients (mean age, 14.99 years; SD, ±1.90 years; boys, 56, 48.7%; girls, 59, 51.3%) adhered to the study protocol and provided pain data over the time period after orthodontic separator placement. An advantage of the mixed-effects models for repeated measures data is that they can handle subject-to-subject variations in the timing of measurements as well as missing data under the missing-at-random assumption; therefore, subjects do not need to provide outcome measurements at exactly the same time points. In our study, the subjects were asked to record their pain intensity as close as possible to the scheduled measurement times. When they failed to record pain at a scheduled time (eg, they were asleep) they would simply record their pain intensity and time of measurement at the first available opportunity. As stated in the methodologic section, we intended to collect 11 observations per subject. The results showed that the average number of observations per subject was 10.5, with a minimum of 9 and a maximum of 11, suggesting that missing data was not a major problem in our study.
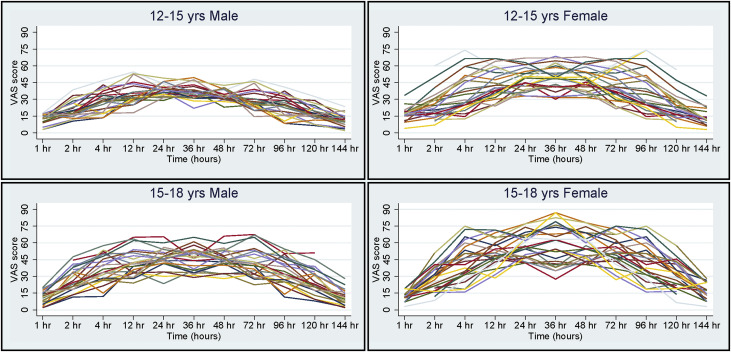
The descriptive statistics showing the demographic characteristics and the clinical data at each time point are shown in Table I . All 4 groups were well matched for number of subjects as well as the mean ages for male and female subjects in the 12- to 15-year and 15- to 18-year age groups. The mean pain score data show that peak pain intensity plateaued for all 4 groups between 24 and 48 hours, and that the mean differences between the 4 groups were also most pronounced during this period. The frequency of analgesic consumption was also the highest at this point. Over the 7-day period as a whole, pain intensity and frequency of analgesic consumption were highest for the 15- to 18-year-old female group and lowest for the 12- to 15-year-old male group. Individual pain trajectories for each group in Figure 1 show substantial between-subject heterogeneity in the VAS scores: some subjects reported greater pain across all occasions than did others. Figure 1 also shows substantial within-subject heterogeneity in the scores: the subjects’ individual pain trajectories are not smooth; rather, there is some time-to-time volatility in their pain profiles.
| Time (h) | Males, 12-15 y n = 28 (24.35%) ∗ |
Females, 12-15 y n = 29 (25.22%) † |
Males, 15-18y n = 28 (24.35%) ‡ |
Females, 15-18 y n = 30 (25.09%) § |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VAS score | Analgesic ¶ | VAS score | Analgesic ¶ | VAS score | Analgesic ¶ | VAS score | Analgesic ¶ | |||||||||
| Mean | SD | Count | % | Mean | SD | Count | % | Mean | SD | Count | % | Mean | SD | Count | % | |
| 1 | 12.5 | 4.0 | 0 | 0 | 14 | 9 | 6 | 20.69 | 8.6 | 6.2 | 4 | 14.29 | 11.1 | 5.9 | 4 | 13.33 |
| 2 | 20.3 | 7.0 | 0 | 0 | 27 | 13 | 5 | 17.24 | 25.7 | 11.6 | 4 | 14.29 | 26.4 | 14.5 | 9 | 30 |
| 4 | 27.6 | 9.4 | 3 | 10.71 | 36 | 19 | 12 | 41.38 | 36.2 | 12.3 | 11 | 39.29 | 42.8 | 19.4 | 18 | 60 |
| 12 | 31.5 | 12.8 | 8 | 28.57 | 44 | 14 | 15 | 51.72 | 40.9 | 11.4 | 15 | 53.57 | 51.1 | 12.1 | 25 | 83.33 |
| 24 | 37.6 | 5.2 | 7 | 25 | 45 | 16 | 22 | 75.86 | 45.2 | 8.9 | 23 | 82.14 | 53.3 | 18.0 | 30 | 100 |
| 36 | 36.5 | 6.4 | 6 | 21.43 | 43 | 21 | 24 | 82.76 | 41.0 | 15.3 | 17 | 60.71 | 56.3 | 23.5 | 25 | 83.33 |
| 48 | 34.5 | 4.8 | 3 | 10.71 | 45 | 16 | 22 | 75.86 | 44.7 | 8.6 | 22 | 78.57 | 52.8 | 18.3 | 30 | 100 |
| 72 | 26.4 | 11.2 | 5 | 17.86 | 43 | 14 | 15 | 51.72 | 41.2 | 12.5 | 15 | 53.57 | 52.5 | 13.4 | 25 | 83.33 |
| 96 | 23.5 | 8.9 | 1 | 3.57 | 36 | 19 | 12 | 41.38 | 34.8 | 11.9 | 10 | 35.71 | 42.8 | 19.4 | 18 | 60 |
| 120 | 17.2 | 6.3 | 0 | 0 | 25 | 13 | 3 | 10.34 | 24.5 | 12.0 | 3 | 10.71 | 29.6 | 16.4 | 14 | 46.67 |
| 144 | 10.9 | 4.7 | 0 | 0 | 11 | 9 | 6 | 20.69 | 8.6 | 7.3 | 4 | 14.29 | 14.9 | 8.8 | 4 | 13.33 |
∗ Average age, 13.5 y (SD = 1.01).
† average age, 13.2 y (SD = 1.04).
‡ average age,16.5 y (SD = 1.02).
§ average age,16.6 y (SD = 0.97).
¶ analgesic count shows the number of subjects in each group who consumed an analgesic at each time point.
The results from the mixed-effects location scale analysis are shown in Table II . The variables included in this final model were based on the best fitting model identified by likelihood ratio tests and the information criterion. The close fit of the mean fitted VAS trajectories to the mean observed VAS trajectories further confirmed the good model fit ( Supplementary Fig 1 ). The histogram and quantile-quantile plots also showed no threat to the random-effects normality assumptions ( Supplementary Fig 2 ).
| Parameter | Variables | Estimate | SE | z | P | 95% CI | |
|---|---|---|---|---|---|---|---|
| Lower | Upper | ||||||
| Mean (average) | Constant | 13.52 | 0.98 | 13.75 | 0.000 | 11.59 | 15.45 |
| Age | −0.61 | 1.74 | −0.35 | 0.728 | −4.02 | 2.81 | |
| Sex | 1.80 | 1.98 | 0.91 | 0.363 | −2.08 | 5.69 | |
| Age×sex | −0.02 | 2.74 | −0.01 | 0.994 | −5.40 | 5.36 | |
| Time | 9.16 | 0.26 | 35.00 | 0.000 | 8.65 | 9.67 | |
| Age×time | 3.88 | 0.39 | 9.91 | 0.000 | 3.11 | 4.64 | |
| Sex×time | 4.32 | 0.46 | 9.47 | 0.000 | 3.42 | 5.21 | |
| Age×sex×time | 0.36 | 0.18 | 2.03 | 0.042 | 0.01 | 0.71 | |
| Time×time | −0.95 | 0.03 | −37.36 | 0.000 | −1.00 | −0.90 | |
| Age×time×time | −0.37 | 0.04 | −9.69 | 0.000 | −0.44 | −0.29 | |
| Sex×time×time | −0.42 | 0.04 | −9.63 | 0.000 | −0.51 | −0.34 | |
| Between-subject variance | Constant | 3.05 | 0.31 | 9.89 | 0.000 | 2.45 | 3.66 |
| Age | 0.79 | 0.42 | 1.88 | 0.060 | −0.03 | 1.61 | |
| Sex | 1.53 | 0.40 | 3.84 | 0.000 | 0.75 | 2.30 | |
| Age×sex | −0.93 | 0.55 | −1.67 | 0.094 | −2.01 | 0.16 | |
| Within-subject variance | Constant | 2.39 | 0.20 | 12.13 | 0.000 | 2.01 | 2.78 |
| Age | 0.22 | 0.21 | 1.06 | 0.289 | −0.19 | 0.63 | |
| Sex | 0.69 | 0.19 | 3.57 | 0.000 | 0.31 | 1.07 | |
| Age×sex | 0.30 | 0.27 | 1.10 | 0.270 | −0.24 | 0.84 | |
| Time | 0.55 | 0.07 | 7.34 | 0.000 | 0.40 | 0.70 | |
| Time×time | −0.06 | 0.01 | −7.64 | 0.000 | −0.07 | −0.04 | |
| Association | Linear association | 0.25 | 0.08 | 3.24 | 0.001 | 0.10 | 0.39 |
| Scale | Sigma | 0.56 | 0.07 | 8.51 | 0.000 | 0.430 | 0.688 |
∗ Variable coding: age (0, 12-15 years; 1, 15-18 years); sex (0, male; 1, female). The constant (intercept) represents time 0 corresponding to the first wave of data: 1 hour after orthodontic separator placement. The between-subject and within-subject variance estimates are on the log scale. The log-likelihood statistic for this model was −4160.6172.
The predicted mean pain trajectories for each group are shown as Figure 2 . The mean initial pain at 1 hour after orthodontic separator placement was 13.52 mm on the VAS for the 12- to 15-year-old male group, and there was no significant main effect of age (estimate, −0.61; P = 0.728; 95% confidence interval [CI], −4.02 to 2.81), sex (estimate, 1.80; P = 0.363; 95% CI, −2.08 to 5.69), or age-sex interaction effect (estimate, −0.02; P = 0.994; 95% CI, −5.40 to 5.36) on the initial pain level.
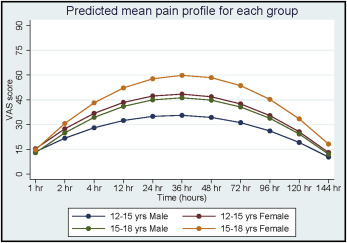
From the initial pain onward, the 12- to 15-year-old male group showed a statistically significant increase in pain with time (linear estimate, 9.16; P = 0.000; 95% CI, −8.65 to 9.67), but this rate decelerated with time (quadratic estimate, −0.95; P = 0.000; 95% CI, −1.0 to −0.90), suggesting an inverted U-shaped mean average pain trajectory ( Fig 2 ).
Compared with the 12- to 15-year-old male group, the 15- to 18-year-old male group (estimate, 3.88; P = 0.00; 95% CI, 3.11 to 4.64) and the 12- to 15-year-old female group (estimate, 4.32; P = 0.000; 95% CI, 3.42 to 5.21) showed significantly steeper rises in pain. The corresponding Cohen d effect size can be estimated as the slope coefficient/√ (between-subject variance + within-subject variance). The required estimates of between-subject and within-subject variance are provided in the later sections of the results.
However, the significant age-sex interaction effect with time (estimate, 0.36; P = 0.042; 95% CI, −0.01 to 0.71) showed that the difference in the rate of increase in pain between the sexes was conditioned on age; as a result, the rate of increase in pain was further increased by 0.36 units in the 15- to 18-year-old female group compared with the 12- to 15-year-old female group. The results for the pairwise comparisons (using Stata’s “lincom” command) to detect the difference in the linear rate of increase in pain among the 4 groups ( Supplementary Table I ) show that the greatest difference was between the 15- to 18-year-old female group and the 12- to 15-year-old male group (estimate, 8.55; P = 0.000; 95% CI, 7.40 to 9.70).
Compared with the 12- to 15-year-old male group, the deceleration was significantly faster for the 15- to 18-year-old male group (estimate, −0.37; P = 0.000; 95% CI, −0.44 to −0.29) and the 12- to 15-year-old female group (estimate, −0.42; P = 0.000; 95% CI, −0.51 to −0.34). For the quadratic trend, the age-sex interaction effect was not included in the model because it led to convergence difficulties. However, a likely reason for this is that the age and sex interactions with the quadratic trend captured the trajectories appropriately and adequately. Therefore, the deceleration in the rate of increase in pain for girls was not conditioned on age, and girls attained higher peak pain intensities in both age groups.
Therefore, compared with the 12- to 15-year-old male group, the 15- to 18-year-old female group experienced the most rapid increase in pain, thereby resulting in the highest peak of pain intensity. However, because of the girls’ faster rate of pain deceleration, the difference in pain intensity between sexes decreased toward the end of the study period.
Interestingly, our findings show a plateau of peak pain intensity for all 4 groups between 24 and 48 hours, with the peak around 36 hours. The fact that time is entered as a polynomial makes it straightforward to predict the actual time at which each group attained the peak level of pain intensity. Full details are provided in the Supplementary Material (equation 16 ), and estimates were obtained using Stata’s “nlcom” command.
The results showed that the times of peak mean pain intensity for the 12- to 15-year-old boys, the 12- to 15-year-old girls, the 15- to 18-year-old boys, and the 15- to 18-year-old girls were 4.83, 4.92, 4.96, and 5.10 on the model’s time scale ( Supplementary Table II ). These numbers imply that the 12- to 15-year-old boys, the 12- to 15-year-old girls, and the 15- to 18-year-old boys attained peak mean pain intensity levels before 36 hours, whereas the 15- to 18-year-old girls reported peak mean pain intensity after 36 hours. The results for the pairwise comparisons to detect the differences in the time of peak mean pain intensity ( Supplementary Table III ) show that the difference was significant between the 15- to 18-year-old female group and the other 3 groups.
The between-subject variance function showed that after we adjusted the VAS scores for time, covariates, and covariates-by-time interaction effects, there was significant remaining variability in terms of the subjects’ individual trajectories about the overall mean average trajectory. Compared with the 12- to 15-year-old boys, the 15- to 18-year-old boys showed greater between-subject variations but not significantly so (estimate, 0.79; P = 0.060; 95% CI, −0.03 to 1.61). However, the 12- to 15-year-old girls were significantly more variable than were the 12- to 15-year-old boys (estimate, 1.53; P = 0.000; 95% CI, 0.75 to 2.30). Interestingly, although not significant, the age-sex interaction effect was negative for the between-subject variance estimate, implying that the 15- to 18-year-old girls were actually less variable than the 12- to 15-year-old girls.
The predicted between-subject variances for the 12- to 15-year-old male, the 12- to 15-year-old female, the 15- to 18-year-old male, and the 15- to 18-year-old female groups were 21.19, 97.47, 44.66, and 84.98, respectively. The standard deviation of the between-subjects variations can be calculated from variance as SD = √variance. Further, the model-implied 95% range for such variations can be calculated as SD*2*1.96. Therefore, the standard deviations (95% range) for the 12- to 15-year-old male, the 12- to 15-year-old female, the 15- to 18-year-old male, and the 15- to 18-year-old female groups between-subjects variation were ±4.60 mm (±18.04 mm), ±9.87 mm (±38.70 mm), ±6.65 mm (±26.07 mm), and ±9.21 mm (±36.13 mm), respectively. Thus, the girls exhibited greater individual heterogeneity in pain than did the boys, and this variation was greatest for the 12- to 15-year-old girls.
The within-subject variance function captures the occasion-to-occasion variations in pain intensity as a function of the evolution of time and covariates (age, sex, and age-sex effect) and provides insight into each subject’s fluctuation in pain intensity around his or her mean pain trajectory. We also examined interactions of the covariates with linear and quadratic time terms, but the estimates were not significant, and there was no improvement in the model fit.
The results show that the degree of within-subject variations exhibited by the typical 12- to 15-year-old boy was significantly related to both the linear (estimate, 0.55; P = 0.000; 95% CI, 0.40 to 0.70) and the quadratic (estimate, −0.06; P = 0.000; 95% CI, −0.07 to −0.04) components of the time trend. Compared with a typical 12- to 15-year-old boy, a 15- to 18-year-old boy showed greater within-subject variance at all times, but this difference was not significant (estimate, 0.22; P = 0.289; 95% CI, −0.19 to 0.63). However, the 12- to 15-year-old female group showed significantly more variable daily pain experience (estimate, 0.69; P = 0.000; 95% CI, 0.31 to 1.07) than the 12- to 15-year-old male group. Although not significant, it is interesting that in contrast to the between-subject variance, the age-sex interaction effect for the within-subject variance was positive (estimate, 0.30; P = 0.270; 95% CI, −0.24 to 0.84); this implies that a typical 15- to 18-year-old girl has greater daily variations in pain than a 12- to 15-year-old girl.
The predicted population-averaged within-subject variances for the 12- to 15-year-old male, the 12- to 15-year-old female, the 15- to 18-year-old male, and the 15- to 18-year-old female groups were 31.96, 63.84, 40.86, and 107.66, respectively. The corresponding standard deviations (95% range) for the 12- to 15-year-old male, the 12- to 15-year-old female, the 15- to 18-year-old male, and the 15- to 18-year-old female groups within-subjects variations were ±5.50 mm (±21.59 mm), ±7.78 mm (±30.51 mm), ±6.22 mm (±24.39 mm), and ±10.11 mm (±39.63 mm), respectively.
In other words, a typical girl has a more erratic series of pain measurements about her individual quadratic trajectory than does a typical boy, and this variation was greatest for the 15- to 18-year-old girls.
The linear random-location effects are positively associated with the within-subjects variance; so, after adjustments for all covariates, subjects with higher mean pain scores tended to have greater pain variability (estimate, 0.25; P = 0.001; 95% CI, 0.10 to 0.39). Finally, the between-subjects random-scale standard deviation, which allows for individual-to-individual heterogeneity in the within-subjects variances remained significant even after adjusting for the time, age, and sex of the subject, suggesting an unexplained component to the within-subjects’ pain variability (estimate, 0.56; P = 0.001; 95% CI, 0.430 to 0.688). Thus, some patients have more erratic pain measurements than others, and this is not explained by their age and sex, nor is it simply related to their overall mean level of pain.
Based on the predicted between-subject and within-subject variances, the ICC can be calculated for each group. The ICC represents the proportion of overall variation in unexplained pain perception that lies between subjects. It is also the expected residual correlation between 2 observations from the same subject and therefore quantifies the remaining clustering or dependency in the data. The ICC values, derived as the between-subject variance divided by the sum of the between-subject and within-subject variances, were calculated for the 12- to 15-year-old male, the 12- to 15-year-old female, the 15- to 18-year-old male, and the 15- to 18-year-old female groups as 0.42, 0.62, 0.54, and 0.46, respectively. Thus, although there was substantial residual clustering for all 4 groups, subjects in the 12- to 15-year-old female group showed disproportionately greater variations in the overall average levels of pain experienced coupled with disproportionately low fluctuations in daily pain perception.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


