Introduction
En-masse sliding mechanics have been typically used for space closure. Because of friction created at the bracket-wire interface, the force system during tooth movement has not been clarified.
Methods
Long-term tooth movements in en-masse sliding mechanics were simulated with the finite element method.
Results
Tipping of the anterior teeth occurred immediately after application of retraction forces. The force system then changed so that the teeth moved almost bodily, and friction occurred at the bracket-wire interface. Net force transferred to the anterior teeth was approximately one fourth of the applied force. The amount of the mesial force acting on the posterior teeth was the same as that acting on the anterior teeth. Irrespective of the amount of friction, the ratio of movement distances between the posterior and anterior teeth was almost the same. By increasing the applied force or decreasing the frictional coefficient, the teeth moved rapidly, but the tipping angle of the anterior teeth increased because of the elastic deflection of the archwire.
Conclusions
Finite element simulation clarified the tooth movement and the force system in en-masse sliding mechanics. Long-term tooth movement could not be predicted from the initial force system. The friction was not detrimental to the anchorage. Increasing the applied force or decreasing the friction for rapid tooth movement might result in tipping of the teeth.
Two methods have been used for extraction space closure. The first is 2-step retraction, which involves canine retraction followed by incisor retraction. The second method is en-masse retraction of the 6 anterior teeth. Recently, Heo et al compared the anchorage losses of the posterior teeth between the 2 methods and showed that en-masse space closure was not detrimental to the anchorage in comparison with 2-step retraction. Huang et al also reported that no significant difference in root resorption was seen between 2-step and en-masse space closure procedures. Since en-masse space closure can reduce treatment duration, it might be considered an advantage over the 2-step retraction method.
En-masse movement has 2 types of mechanics. The first is segmental mechanics, in which the anterior teeth are retracted directly with a spring such as a T-loop space closure spring. In this method, a complicated design of the spring is necessary to achieve bodily tooth movement. The second type is sliding mechanics, in which the anterior teeth move together with an archwire guided by the brackets placed on the posterior teeth. This method can easily achieve bodily tooth movement.
In sliding mechanics, friction occurs at the wire-bracket interface. Many measurements of the friction force have been carried out for various combinations of wires and brackets. The friction dissipates some of the applied force and decreases the speed of the tooth movement. It is difficult to know whether the magnitude of the applied force is sufficient to allow tooth movement. Application of high magnitude force, in an attempt to overcome the friction, might increase the movement of the anchor teeth, and the belief has been that friction is detrimental to anchorage.
In 2-step retraction, which involves canine retraction with sliding mechanics, mechanical simulation by using a finite element method has been carried out, and the forces transferred to the teeth have been estimated. The results showed that friction had no effect on the movement ratio of the canine and anchor teeth. The friction acted not only on the canine but also on the anchor teeth. The latter friction prevented the anchor teeth from moving. The friction was not detrimental to the anchorage. This finding was also reported by Southard et al.
However, few studies have been carried out on en-masse retraction with sliding mechanics. The force system and the tooth movements have not been fully clarified. Recently, Tominaga et al calculated the initial tooth movement in en-masse sliding mechanics using a precise finite element model and clarified the types of tooth movement immediately after force application. However, the force acting on the teeth can vary during orthodontic tooth movement. Therefore, in this study, we calculated the long-term tooth movements in en-masse sliding mechanics. For this purpose, the simulation method proposed in a previous article was used, and the force system and the tooth movements were illustrated. These results will be helpful to understand the mechanism of en-masse sliding mechanics.
Material and methods
We used the sliding mechanics described by McLaughlin and Bennett and made a finite element model as shown in Figure 1 . Assuming symmetry for both sides of the arch, a model of only the left side was fabricated. The archwire was made from a stainless steel wire of 0.019 × 0.025 in (Young’s modulus, 200 GPa) and divided into 3-dimensional elastic-beam elements.
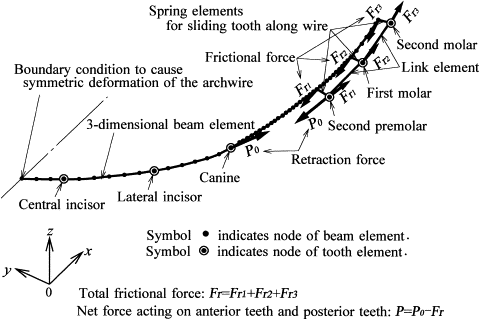
The mechanical response of a tooth supported by the periodontal ligament (PDL) is replaced by the tooth element. It represents the 3-dimensional movement produced by elastic deformation of the PDL when forces and moments act on a tooth. The calculation method of the tooth element was explained in detail in the previous article. In this method, the tooth and the alveolar bone are assumed to be rigid bodies, whereas the PDL is a linear elastic film (Young’s modulus, 0.2 MPa; Poisson’s ratio, 0.47) with a uniform thickness of 0.2 mm. To calculate the tooth elements, the surface models of the tooth are necessary. They were made based on a dental study model (i21D-400C, Nissin Dental Products, Kyoto, Japan).
Nodes of the anterior tooth elements are connected directly to the archwire nodes to prevent them from sliding on each other. Alternatively, nodes of the posterior tooth elements are connected to the archwire nodes with spring elements, which allow the teeth to slide closely along the archwire. The clearance between wire and bracket slot is disregarded in this model. Retraction forces of Po =1 N are applied to the canine and the premolar brackets. The premolar and the molars are connected with link elements, by which the force applied to the premolar is delivered to the molars.
Kinetic friction is produced when the archwire slides through the bracket slots of the premolar and molars. Friction forces in the mesial direction act on the archwire, and those in the distal direction act on the brackets. The friction forces at the premolar and molars are denoted as Fr 1 , Fr 2 , and Fr 3 . Absolute values of net forces acting on the anterior and posterior teeth are the same, and they are obtained by subtracting the total friction force Fr = ( Fr 1 + Fr 2 + Fr 3 ) from the retracting force Po , P = (Po – Fr) . The calculation method of the friction force was explained in a previous article. The bracket width is assumed to be 3 mm, and the frictional coefficient is assumed to be μ = 0.2 based on the experimental data.
In the first step, forces and moments acting on the teeth are calculated by using the finite element model ( Fig 1 ). In the second step, for each tooth, the amount of orthodontic tooth movement is calculated based on the stress induced in the PDL. Then the tooth is displaced by this amount. By repeating this procedure, the teeth move step by step. The force system acting on the teeth is updated with the tooth movement. The detailed calculation method was explained in previous articles. In this method, orthodontic tooth movement is produced by resorption and apposition of the alveolar bone (bone remodeling). The bone remodeling rate is assumed to be in proportion to the mean stress, σ m , in the PDL. Denoting the amount of bone resorption (and apposition) (μm) per unit of time (day) and unit of stress (kPa) by a coefficient, C , (μm/[day·kPa]), tooth movement depends on the parameter CT , where T is the elapsed time. Because C is an unknown value at the present time, the progress of tooth movement is indicated by the parameter CT .
Results
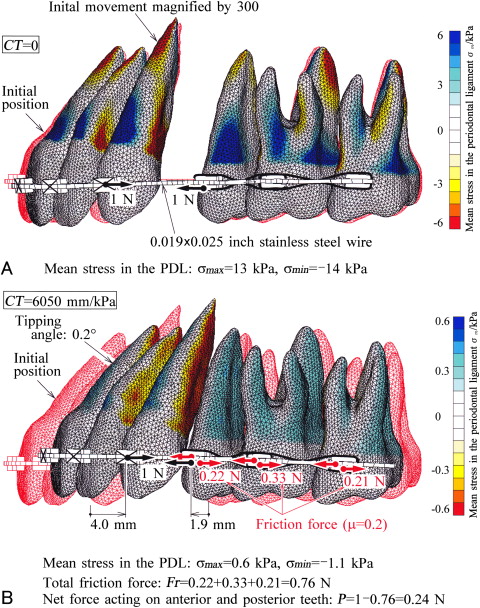
Immediately after the application of forces of Po = 1 N to the brackets of the canine and the second premolar, the movement of the teeth is illustrated in Figure 2 , A . The initial tooth positions are illustrated with hidden red lines . To indicate the difference in tooth positions before and after the movements, the actual displacements of the teeth were magnified 300 times. At this time, friction forces were not produced, so that the retraction forces acted directly on the anterior and posterior teeth. Distributions of mean stress in the PDL are indicated by color contours . The maximum and minimum stresses, σ max and σ min , are indicated in the figure. When the canine bracket moved distally by 4.0 mm, the premolar bracket moved mesially by 1.9 mm ( Fig 2 , B ). The tipping angle of the central incisor was only 0.2°; thus, the anterior teeth moved bodily. The friction forces produced at each bracket were 0.22, 0.33, and 0.21 N. Since total frictional force became 0.76 N, net forces acting on the anterior and posterior teeth were 0.24 N.

Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


