Material and methods

A potentially important factor influencing the effectiveness of initial orthodontic alignment is the bracket system and, specifically, the mode of archwire ligation. The 2 main bracket systems include those in which wires are engaged with either elastics or ligatures (conventional brackets) and self-ligating brackets, incorporating a self-engaging mechanism, either active or passive. The treatments we intend to compare are applicable, in principle, to any patient who needs orthodontic therapy; hence, the treatments can be considered as competing. Several trials have been published comparing self-ligating systems, such as In-Ovation-R (Dentsply GAC International, Islandia, NY), Damon (Ormco Corp, Orange, Calif), and Smart-Clip (3M Unitek, Monrovia, Calif), with conventional systems. The comparisons are typically limited to 2 groups, such as Damon vs conventional, or Smart-Clip vs conventional, and so forth. In this example, we will use NMA to compare all interventions simultaneously, allowing them to be ranked in order of effectiveness.

The following selection criteria were applied.

• 1.

  Study design: randomized clinical trials (RCTs) and controlled clinical trials (CCTs), including split-mouth designs.

• 2.

  Participants: patients with full-arch, fixed, and bonded orthodontic appliances.

• 3.

  Interventions and comparators: various types of self-ligating and conventional brackets.

• 4.

  Outcome measures: millimeters of crowding alleviated during the initial alignment stage per unit of time.

The following electronic databases were searched: MEDLINE (1966 to December 2012, Appendix 1), EMBASE (1980 to December 2012), the Cochrane Oral Health Group’s Trials Register (December 2012), and the Cochrane Central Register of Controlled Trials (CENTRAL, Cochrane Library Issue 1, 2013) without language restrictions. Unpublished articles were searched electronically using ClinicalTrials.gov ( www.clinicaltrials.gov ), the National Research Register ( www.controlled-trials.com ), and Pro-Quest Dissertation Abstracts and Thesis database ( www.proquest.com ) with the term orthodontic . Conference proceedings and abstracts were also accessed when possible. Authors were contacted to identify unpublished or ongoing clinical trials and to clarify results if necessary. Reference lists of the included studies were screened for relevant research.

Assessment of research for inclusion in the review, assessment of risk of bias, and extraction of data were performed, and disagreements were resolved by discussion. Seven criteria were considered to grade the risk of bias of each study: random sequence generation, allocation concealment, blinding of participants and personnel, blinding of assessors, incomplete outcome data, selective reporting of outcomes, and other potential sources of bias.

A data extraction form was developed to record study design, observation period, participants, interventions, outcomes, and outcome data of interest, including extractions. The clinical and methodologic heterogeneity of the included studies was judged by assessing the treatment protocol, particularly participants and setting; intervention details, such as materials used; follow-up; timing of data collection; and measurement techniques.

The primary outcome assessed was the amount of tooth movement in millimeters per month. This outcome was calculated in each primary study by dividing the amount of crowding resolved by the number of days of follow-up during initial alignment and then scaled to provide a monthly rate. When the standard deviation of the mean difference was not reported in the studies, the following formula was used to approximate it:

where sdbefore
s d b e f o r e
and sdafter
s d a f t e r
are the standard deviations before and after the alignment stage, respectively, and r
r
is the correlation coefficient between the before and after measurements. The correlation coefficient was calculated from available patient data when necessary. To reduce potential bias because of lack of randomization in CCTs, estimates adjusted for the impact of potential effect modifiers (eg, bracket type, age, sex, and Angle classification as covariates) were calculated from individual patient data supplied by the trial authors. For split-mouth designs, the mean difference from the paired observations was calculated along with the corresponding standard deviation. The relative treatment effect was calculated as the difference in the monthly rate of alignment between the compared interventions.

The combination of direct and indirect evidence is considered reasonable when the selected treatments are exchangeable, and any study participant is eligible to receive any competing intervention. The key assumption for applying NMA is that there are no important differences in the distribution of possible effect modifiers across trials investigating various comparisons, other than the particular treatments being assessed. The synthesis of studies directly comparing 2 treatments makes sense only when the studies are sufficiently similar in terms of important clinical and methodologic characteristics (effect modifiers). Only when this is the case can we assume that the intervention effects are transitive: ie, we can estimate a comparison via a common comparator ( Fig 1 ). For example, a valid indirect comparison for active vs passive appliances requires that the studies considering active vs conventional appliances and passive vs conventional appliances are similar with respect to the distribution of effect modifiers such as severity of crowding at baseline, age, sample size, and study quality. Transitivity can be viewed as an extension of clinical and methodologic homogeneity to comparisons across groups of studies comparing different treatments. The plausibility of the transitivity assumption requires clinical judgment to decide whether differences in the distributions of the effect modifiers across studies are large enough to make NMA invalid.

Direct and indirect comparisons.

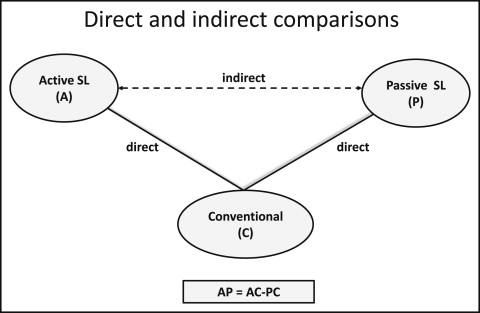
One possible effect modifier is the degree of bias in the included studies; for instance, blinding might be less feasible with some treatments compared with others, and this might influence the results. To evaluate this assumption, we present the location and dispersion characteristics (eg, medians and ranges) of effect modifiers across treatment comparisons. However, evaluation of the assumption can be complicated by failure to report effect modifiers in primary studies or because a limited numbers of studies per comparison does not permit a reasonable judgment.

Using indirect evidence, it is possible to estimate the relative effectiveness of 2 treatments, despite the lack of studies directly comparing specific interventions. For example, we can compare Damon ( D ) with Smart-Clip ( S ) using conventional ( C ) as a common comparator ( Fig 2 ). The meta-analytical effect estimates of Damon vs conventional and Smart-Clip vs conventional trials are denoted as ˆμDDC
μ ˆ DC D
and ˆμDSC
μ ˆ SC D
, respectively, where the superscript refers to the direct estimate, and the subscript refers to the pair-wise comparison (Damon vs conventional, and Smart-Clip vs conventional). The variances of the direct meta-analytic estimates are denoted with ˆvDCS
v ˆ CS D
and ˆvDCD
v ˆ CD D
. An indirect estimate ˆμIDS
μ ˆ DS I
for the comparison of Damon vs Smart-Clip can be obtained by subtracting the meta-analytical estimate of conventional vs Damon from the meta-analytical estimate of conventional vs Smart-Clip.

Network of eligible comparisons for NMA for effectiveness. The size of the nodes corresponds to the number of trials relating to each bracket system. The more trials concerning a bracket system, the larger the node for this intervention. The directly comparable interventions are linked with a line. The thickness of the line corresponds to the number of trials about this comparison. The larger the number of the trials considering this comparison, the thicker the line that links these interventions. It is obvious that the system most frequently encountered is the conventional followed by Damon; the most frequent comparison is Damon vs conventional. The number of trials investigating this comparison and the total number of randomized participants (in parentheses) are presented on each link.

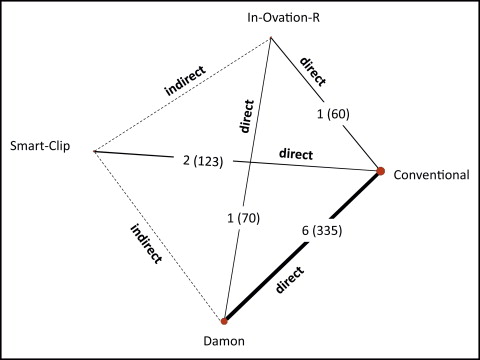
The variance of the indirect estimate is simply the sum of the variances of the 2 direct estimates, as long as the direct estimates are independent.

Then a 95% CI for the indirect estimate can be obtained as follows.

If both direct and indirect evidence is available for a comparison (as is the case of Damon vs In-Ovation-R), we can combine these 2 sources of evidence by taking the weighted average of the direct ˆμDDI
μ ˆ D I D
and the indirect estimates ˆμIDI(=ˆμDCI−ˆμDCD)
μ ˆ D I I ( = μ ˆ C I D − μ ˆ C D D )
. This combination is known as mixed evidence, and it will be denoted as μ ˆ D I M
μ ˆ D I M
. Using the inverse-variance method, the mixed relative treatment effect for Damon vs In-Ovation-R is calculated as follows

where w ˆ D I D = 1 / v ˆ D I D
w ˆ D I D = 1 / v ˆ D I D
and w ˆ D I I = 1 / v ˆ D I I
w ˆ D I I = 1 / v ˆ D I I
are the weights for the direct and indirect evidence, respectively.

The variance of μ ˆ D I M
μ ˆ D I M
is calculated by

Stay updated, free dental videos. Join our Telegram channel

Join