Material and methods
Ninety NiTi-based closed-coil springs were used, 30 of each of the following types: (1) Nitinol (code 146-150, 3M Unitek, Monrovia, Calif), (2) Ni-Ti (code 222-5612, Ormco, Glendora, Calif), and (3) RMO (code F00321 , Rocky Mountain Orthodontics, Denver, Colo). According to the manufacturers’ indications, all closed-coil springs had the wire diameters of 0.010 in (0.25 mm), and the lumen diameter was 0.030 in (0.76 mm), with a total length of each spring of 12 mm. The force exerted by these closed-coil springs was given by only 1 manufacturer as 150 gf (Nitinol). All coil springs used in this study were selected at random from a large number of samples.
The study design is illustrated in Figure 1 . Each coil-spring group was divided into 2 equal subgroups of 15 springs, which were subjected to prolonged and constant strain under an extension of either 6 mm (50%) or 18 mm (150%) over the initial length of 12 mm. Moreover, to simulate the aging that occurs in an oral environment, the coil springs of the 3 groups, and thus for both subgroups in each group, were kept in artificial saliva at 37°C and subjected to 2 sessions of thermocycling, on days 22 and 45 after the start of the strain. Curves of deactivation forces from both extension subgroups were recorded initially, before the start of the strain (baseline) and again on days 22 and 45, immediately after the thermocycling sessions. The coil springs in the 50% strain subgroups were never extended beyond this value.
To hold the coil springs at 50% and 150% strain over the study period, a customized stainless steel jig was prepared. This jig included a base, onto which 3 arrays of 15 parallel posts were fixed. The distances between the arrays were set to extend the coil springs to either 50% or 150% above their initial 12-mm length. After we carefully mounted the coil springs on the jig according to their strains, the whole jig and springs were immersed in the artificial saliva, which contained 6.8 mmol/L sodium chloride, 5.4 mmol/L potassium chloride 5.4 mmol/L calcium chloride, 5.0 mmol/L monosodium phosphate, 0.021 mmol/L sodium sulfide, and 16.7 mmol/L urea.
Each of the 2 thermocycling treatment sessions (days 22 and 45) included 1000 temperature cycles from 5°C to 55°C (Thermo Haake Willytech, SD Mechatronik, Feldkirchen-Westerham, Germany), with the springs cyclically immersed in each thermal bath for 30 seconds, with 2 seconds at air temperature between immersions, to reproduce temperature variations that can occur in the mouth when consuming cold and hot foods and beverages, respectively.
A universal testing machine (SUN 500, Galdabini, Cardano al Campo [VA], Italy) was used to measure the loads produced by the coil springs according to the distances the crossheads travelled (deflection rates) and the loads generated (deactivation forces) that were automatically recorded and plotted as x and y scatter plots. After each coil spring had been mounted on the crossheads of the testing machine by using a pair of hooks, they were extended to either 50% or 150% of their initial lengths (to 18 or 30 mm, respectively, according to their strain subgroup) at a rate of 0.25 mm per second. Since only the force produced during deactivation of the extended spring is exerted by the spring in clinical situations, the analysis of the generated loads was conducted during the rebound cycle (deactivation), when the springs were allowed to return to their original lengths at the same speed (with load recordings at every 0.1 mm of deflection). Moreover, the transfers from the customized stainless jig to the testing machine and back to the jig were carried out carefully to prevent any uncontrolled mechanical stress to the coil springs.
Statistical analysis
GraphPad Prism (version 5, GraphPad Software, La Jolla, Calif) and the Statistical Package for Social Sciences software (version 13.0, SPSS, Chicago, Ill) were used for data analysis. After testing for the normality of the data, parametric methods were used, including the Shapiro-Wilks test and Q-Q normality plots; the equality of variance among the data sets was also tested by using the Levene test.
A 1-sample t test was run to evaluate the significance of the differences in the baseline load extensions of 50% and 150% in the 2 strain subgroups with the load deflection of 150 gf reported by only 1 manufacturer.
A 3-way analysis of variance (ANOVA) was performed to assess the differences in the load deflections at the discrete extensions of 50% and 150% over the initial length (in the 50% and 150% strain subgroups, respectively). The 3 factors in the ANOVA were the time point as a repeated factor, and the coil-spring group and the strain, as independent factors. Pairwise comparisons between the time points in each coil-spring groups and strains were performed by using the Bonferroni-corrected paired-sample t test. The pairwise comparisons between the coil-spring groups at each time point and strain were performed by using the Bonferroni-corrected independent-sample t test. The same independent-sample t test was used to evaluate the significance of the differences in load deflections between the strains in each coil-spring group and at each time point.
A P value less than 0.05 was used for rejection of the null hypothesis.
To quantitatively describe the deactivation forces and to objectively identify nonlinear (superelasticity) ranges of activation in each coil-spring group, time point, and strain, the full data sets of the deactivation forces were fit by linear regression. Since the expected behavior for NiTi-based coil springs on deflection would be a rapid increase followed by a plateau phase (again, for superelasticity), segmental linear regression was used. For this function, 2 linear regressions were used to fit the data. The choice of the end point between the 2 regressions was based on the highest R 2 value achievable. If segmental linear regression showed an R 2 value below 0.99, alternative polynomial regressions were used to fit the data.
Results
The loads at the discrete deflections of 50% and 150% in the subgroups are shown in the Table . At baseline, the loads exerted by the NiTi-based coil springs investigated here varied from 99.8 to 245.1 gf for the RMO (50% strain) and the Ni-Ti (150% strain) types ( Table ). All loads were significantly different compared with the 1 manufacturer’s reported 150 gf (all at P <0.001) for all coil-spring groups.
| Strain | Time point | Nitinol | Ni-Ti | RMO |
|---|---|---|---|---|
| 50% | Baseline | 114.2 ± 3.5 | 193.8 ± 6.9 | 99.8 ± 18.2 |
| 22 days | 114.0 ± 3.5 | 195.1 ± 5.2 | 126.7 ± 14.8 | |
| 45 days | 105.3 ± 14.6 | 179.7 ± 12.4 | 125.3 ± 14.3 | |
| NS | a | b | ||
| 150% | Baseline | 127.1 ± 3.7 ∗ | 245.1 ± 13.3 ∗ | 182.3 ± 14.0 ∗ |
| 22 days | 126.5 ± 7.1 ∗ | 241.3 ± 9.6 ∗ | 195.5 ± 14.1 ∗ | |
| 45 days | 128.2 ± 7.6 ∗ | 221.8 ± 8.3 ∗ | 178.8 ± 17.2 ∗ | |
| NS | a | c |
∗ Statistically significant difference from the corresponding value at 150% strain.
For the load deflections at the 3-way ANOVA level, all time points, coil-spring groups, and strain factors yielded statistically significant differences in load deflections (F 2;168 = 16.3, P <0.001; F 2;84 = 1799.2, P <0.001; and F 1;84 = 1136.6, P <0.001, respectively). Also, among the 2-way and 3-way interactions, all reached statistically significant levels (at least P <0.05; results not shown).
In the pairwise comparisons in both strains, no significant differences were seen between the time points for the Nitinol group ( Table ). In contrast, for the Ni-Ti group, the load deflections recorded at 45 days were significantly lower compared with the corresponding baseline and 22-day values in both the 50% and 150% strains ( Table ). For the RMO group, the load deflections recorded at both days 22 and 45 were greater than the corresponding baseline values for the 50% strain ( Table ). Also, in the 150% strain, the load deflection recorded at 45 days was significantly lower than the corresponding value at 22 days. Moreover, in the pairwise comparisons between the coil-spring groups, the load deflections showed statistically significant differences at each time point at both 50% and 150% strains, generally with the greatest and lowest values recorded in the Ni-Ti and Nitinol groups, respectively (all at least P <0.05; Table ). All load deflections recorded at the 150% strain were significantly greater than the corresponding values recorded at the 50% strain ( Table ).
The curves of the deactivation forces of the coil-spring groups are shown in Figure 2 , in relation to time and strain.
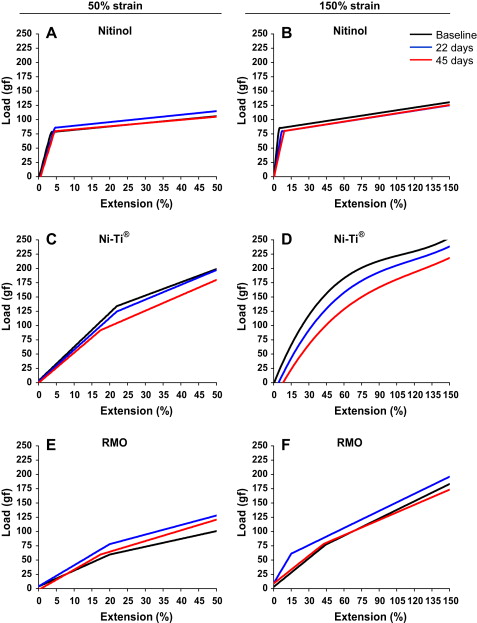
Generally, the Nitinol and RMO groups showed similar behaviors between the strains at each time point and among the time points in each strain. All data can be fitted to segmental linear regression, with R 2 always above 0.991 ( Fig 2 , A, B, E, and F ). In contrast, the Ni-Ti coil-spring groups showed notably different behavior according to the strain, with the 50% and 150% strain subgroup data fitted to segmental linear regressions ( Fig 2 , C ) and third-order functions ( Fig 2 , D ), respectively (all with R 2 above 0.996). Moreover, in the same 150% strain subgroup, an evident change in loads was seen among the time points ( Fig 2 , D ).
Only the Nitinol group showed a superelasticity phase, which started from the maximum strain recorded (at 50% or 150%) to less than about 5% (about 0.5 mm of 12 mm) of residual extension, with only a modest decrease in the loads seen across the full range of deflection. In contrast, the other 2 coil-spring groups showed no superelasticity phase of activation under any experimental condition. With the 50% strain subgroup of the Ni-Ti coil spring ( Fig 2 , C ) and the RMO coil springs in both strain subgroups ( Fig 2 , E and F ), almost proportional phases of activation were seen. In the Ni-Ti coil springs, the 150% strain subgroup had mixed behavior, with a progressive decay in the deactivation forces from baseline to 45 days.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


