where κ is the force constant associated with the chemical bond and μ is the reduced mass: μ = m A*m B/(m A + m B) with m A and m B the mass of atoms A and B. For more complex molecular species, different types of vibrations are possible, which can be determined theoretically [1]. Two types of vibrations with different energy domains are recognized for molecular species other than diatomic ones: stretching vibrations, corresponding to an elongation of chemical bonds, and bending vibrations, corresponding to angular variation between two chemical bonds. Stretching vibrations exhibit a higher energy than the bending ones.
In crystalline solids several types of vibration may occur. In addition to acoustic modes, two main types are identified, “internal vibrations” associated with molecules and molecular ions with covalent bonds that are present in the solid and “external vibrations” corresponding to the vibrations of species and ions in their crystallographic site [2–4]. Internal vibrations are generally close to the vibration energy of the free molecule/ions and allow the identification of molecular species in the solid. However, variations will appear in the energies of internal vibrations and in their relative intensities which depend on the environments of these molecular species in the solid. Such variations allow a precise identification of mineral structures in most cases. Although external vibration modes also depend on the crystal structure, their energy is lower than that of internal vibrations, and they are more easily accessed using Raman spectroscopy. Among these external vibrations, two types of movements may be recognized: translation modes and libration modes, which can be viewed as partial rotation of molecular groups in the crystal. Libration movements of OH− ions and H2O molecules occur at a relatively high energy compared to non-protonated molecules, and the corresponding lines are frequently found among the internal vibrations of other species like phosphate or carbonate. To complete the description of vibrational spectra, overtone and combination lines, which involve multi-quanta excitations, can be observed, although with much weaker intensities than fundamental lines.
The main molecules and molecular ions found in calcium phosphates are orthophosphate groups: PO4 3−, HPO4 2−, 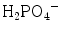 and also H2O, OH−, CO3 2−. The vibrational characteristics of the “free” CO3 2− and PO4 3− ions are shown in Table 8.1 [5, 6], with the symmetry group and vibrational domains. We will use the denominations of the spectroscopic domains of the free molecules/ions to describe and discuss the different spectra in this paper. Although specific domains can be used for protonated phosphate species [5, 7], the P–O vibrational regions remain close to those of the PO4 3− group and they will be discussed by reference to this ion. In protonated species additional lines are expected due to the O–H bond. The stretching of the O–H bonds in HPO4 2− and
and also H2O, OH−, CO3 2−. The vibrational characteristics of the “free” CO3 2− and PO4 3− ions are shown in Table 8.1 [5, 6], with the symmetry group and vibrational domains. We will use the denominations of the spectroscopic domains of the free molecules/ions to describe and discuss the different spectra in this paper. Although specific domains can be used for protonated phosphate species [5, 7], the P–O vibrational regions remain close to those of the PO4 3− group and they will be discussed by reference to this ion. In protonated species additional lines are expected due to the O–H bond. The stretching of the O–H bonds in HPO4 2− and 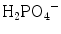 groups are generally broad and appear with a low to medium intensity. However, the P-(OH) bonds in HPO4 2− and
groups are generally broad and appear with a low to medium intensity. However, the P-(OH) bonds in HPO4 2− and 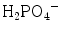 are longer and weaker than the P–O bond in the PO4 3− ion, and the corresponding stretching bands are shifted towards lower wavenumbers. These bands are very sensitive to hydrogen bonding [5, 8, 9]. In contrast the weakening of the P–OH bond is associated with a strengthening of the remaining P–O bonds, whose stretching vibrations are shifted towards higher wavenumbers, whereas bending vibrations are shifted towards lower wavenumbers. The symmetry alterations induced by protonation occurring in HPO4 2− can conveniently be described using distorted PO4 edifices belonging to C3v symmetry (although the symmetry of the real free ions is lower). These species have been included in Table 8.1.
are longer and weaker than the P–O bond in the PO4 3− ion, and the corresponding stretching bands are shifted towards lower wavenumbers. These bands are very sensitive to hydrogen bonding [5, 8, 9]. In contrast the weakening of the P–OH bond is associated with a strengthening of the remaining P–O bonds, whose stretching vibrations are shifted towards higher wavenumbers, whereas bending vibrations are shifted towards lower wavenumbers. The symmetry alterations induced by protonation occurring in HPO4 2− can conveniently be described using distorted PO4 edifices belonging to C3v symmetry (although the symmetry of the real free ions is lower). These species have been included in Table 8.1.
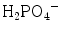 and also H2O, OH−, CO3 2−. The vibrational characteristics of the “free” CO3 2− and PO4 3− ions are shown in Table 8.1 [5, 6], with the symmetry group and vibrational domains. We will use the denominations of the spectroscopic domains of the free molecules/ions to describe and discuss the different spectra in this paper. Although specific domains can be used for protonated phosphate species [5, 7], the P–O vibrational regions remain close to those of the PO4 3− group and they will be discussed by reference to this ion. In protonated species additional lines are expected due to the O–H bond. The stretching of the O–H bonds in HPO4 2− and
and also H2O, OH−, CO3 2−. The vibrational characteristics of the “free” CO3 2− and PO4 3− ions are shown in Table 8.1 [5, 6], with the symmetry group and vibrational domains. We will use the denominations of the spectroscopic domains of the free molecules/ions to describe and discuss the different spectra in this paper. Although specific domains can be used for protonated phosphate species [5, 7], the P–O vibrational regions remain close to those of the PO4 3− group and they will be discussed by reference to this ion. In protonated species additional lines are expected due to the O–H bond. The stretching of the O–H bonds in HPO4 2− and 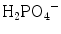 groups are generally broad and appear with a low to medium intensity. However, the P-(OH) bonds in HPO4 2− and
groups are generally broad and appear with a low to medium intensity. However, the P-(OH) bonds in HPO4 2− and 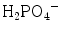 are longer and weaker than the P–O bond in the PO4 3− ion, and the corresponding stretching bands are shifted towards lower wavenumbers. These bands are very sensitive to hydrogen bonding [5, 8, 9]. In contrast the weakening of the P–OH bond is associated with a strengthening of the remaining P–O bonds, whose stretching vibrations are shifted towards higher wavenumbers, whereas bending vibrations are shifted towards lower wavenumbers. The symmetry alterations induced by protonation occurring in HPO4 2− can conveniently be described using distorted PO4 edifices belonging to C3v symmetry (although the symmetry of the real free ions is lower). These species have been included in Table 8.1.
are longer and weaker than the P–O bond in the PO4 3− ion, and the corresponding stretching bands are shifted towards lower wavenumbers. These bands are very sensitive to hydrogen bonding [5, 8, 9]. In contrast the weakening of the P–OH bond is associated with a strengthening of the remaining P–O bonds, whose stretching vibrations are shifted towards higher wavenumbers, whereas bending vibrations are shifted towards lower wavenumbers. The symmetry alterations induced by protonation occurring in HPO4 2− can conveniently be described using distorted PO4 edifices belonging to C3v symmetry (although the symmetry of the real free ions is lower). These species have been included in Table 8.1.
Table 8.1
Vibrational characteristics of molecular ions involved in calcium phosphates
|
Vibrational domains, symmetry, and activity of the free ions (R: Raman activity and IR: infrared activity)
|
||||
|---|---|---|---|---|
|
Molecular ion (symmetry)
|
ν 1
|
ν 2
|
ν 3
|
ν 4
|
|
PO4 3− (Td)
|
A1 (R)
|
E (R)
|
T2 (IR, R)
|
T2 (IR, R)
|
|
Position (cm−1)
|
938
|
420
|
1,017
|
567
|
|
HPO4 2− (C3v)
|
A
|
E
|
A + E
|
A + E
|
|
(IR, R)
|
(IR, R)
|
(IR, R) (IR, R)
|
(IR, R) (IR, R)
|
|
|
Positions (cm−1)
|
988
|
394
|
862 1,076
|
537 537
|
|
CO3 2− (D3h)
|
A′1
|
A″ 2
|
E′
|
E′
|
|
(R)
|
(IR)
|
(IR, R)
|
(IR, R)
|
|
|
Positions (cm−1)
|
1,064
|
879
|
1,415
|
680
|
The vibrational modes of “free” molecular ions and molecules are conveniently determined using molecular group theory [1], which is used to name and distinguish the vibrational modes. Group theory also allows determination of the infrared (IR) and Raman (R) observance of the vibrational modes, their “activity,” which is related to the physical interactions between electromagnetic radiations and vibrational energy levels involved in these spectroscopic methods [2–4].
In crystalline solids two main alterations have been identified: the site symmetry effect and the factor group symmetry [2–4]. The site symmetry effect corresponds to an alteration in vibrational energy levels due to the symmetry lowering of the “free” molecule or polyatomic ion related to its position in a well-defined crystallographic site; these effects are shown in Tables 8.2, 8.3, and 8.4 for different crystalline calcium phosphates in different structures [5, 9–14]. Considering PO4 3− ions in apatites with a hexagonal unit cell (space group P63/m; Table 8.3), for example, the site symmetry is Cs, as only a symmetry plane is preserved from the original tetrahedral symmetry. In consequence, the degeneracy of vibrational modes E (degeneracy: 2) and T2 (degeneracy: 3) of the “free” PO4 3− species is raised, and instead of one vibrational level, several non-degenerated modes occur. All these vibrational modes are active in IR and R and a “splitting” of the ν2, ν3, and ν4 lines is predicted. In addition, ν1 and ν2 modes are now active in IR, although they were not observed for the free ion.
Table 8.2
Internal vibrations of phosphate groups in non-apatitic calcium phosphates of interest (PO4 3−-containing compounds)
|
Tetracalcium phosphate (TTCP); Ca4(PO4)2O; monoclinic P21 [10]
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry: C1
|
A(IR-R)
|
2A(IR-R)
|
3A(IR-R)
|
|
Factor group: C2
|
2A(IR-R)
|
4A(IR-R)
|
6A(IR-R)
|
|
2B(IR-R)
|
4B(IR-R)
|
6B(IR-R)
|
|
|
Number of lines IR
|
4
|
8
|
12
|
|
Number of lines R
|
4
|
8
|
12
|
|
α-Tricalcium phosphate (α-TCP); Ca3(PO4)2; monoclinic P21/a [12]
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry: C1
|
A(IR,R)
|
2A(IR-R)
|
3A(IR-R)
|
|
Factor group: C2h
|
12Ag(R)
|
24Ag (R)
|
36Ag(R)
|
|
12Au(IR)
|
24Au (IR)
|
36Au(IR)
|
|
|
12Bg(R)
|
24Bg (R)
|
36Bg(R)
|
|
|
12Bu(IR)
|
24Bu (IR)
|
36Bu(IR)
|
|
|
Number of lines IR
|
24
|
48
|
72
|
|
Number of lines R
|
24
|
48
|
72
|
|
β-Tricalcium phosphate (β-TCP); Ca3(PO4)2; trigonal R3c [12]
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry C3
|
A(IR-R)
|
E(IR-R)
|
A(IR-R)
|
|
E(IR-R)
|
|||
|
Site symmetry C1
|
A(IR-R)
|
2A(IR-R)
|
3A(IR-R)
|
|
Factor group C3v
|
3A1(IR-R)
|
2A1(IR-R)
|
5A1(IR-R)
|
|
E(IR-R)
|
4E(IR-R)
|
5E(IR-R)
|
|
|
Number of lines IR
|
4
|
6
|
10
|
|
Number of lines R
|
4
|
6
|
10
|
Table 8.3
Internal vibrations of phosphate groups in apatites for different structures and symmetries
|
Apatite; hexagonal P63/m [11]
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry: Cs
|
A′(IR-R)
|
A′(IR-R), A″(IR-R)
|
2A′(IR-R), A″(IR-R)
|
|
Factor group: C6h
|
Ag (R), E2g (R), Bu E1u(IR),
|
Ag(R), E2g(R), Bu, E1u(IR), Bg, E1g(R), Au (IR), E2u
|
2Ag(R), 2E2g(R), 2Bu, 2E1u(IR), Bg, E1g(R), Au (IR), E2u
|
|
Number of lines IR
|
1
|
2
|
3
|
|
Number of lines R
|
2
|
3
|
5
|
|
Apatite; hexagonal P63 [12]
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry: C1
|
A (IR,R)
|
2A (IR-R)
|
3A (IR-R)
|
|
Factor group: C6
|
A(IR-R), B, E1(IR-R), E2(R)
|
2A(IR-R), 2B, 2E1(IR-R), 2E2(R)
|
3A(IR-R), 3B, 3E1(IR-R), 3E2(R)
|
|
Number of lines IR
|
2
|
4
|
6
|
|
Number of lines R
|
3
|
6
|
9
|
|
Apatite; monoclinic P21/b
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry C1
|
A(IR,R)
|
2A(IR-R)
|
3A(IR-R)
|
|
Factor group C2h
|
3Ag(R), 3Bg(R), 3Au(IR), 3Bu(IR)
|
6Ag(R), 6Bg(R), 6Au(IR), 6Bu(IR)
|
9Ag(R), 9Bg(R), 9Au(IR), 9Bu(IR)
|
|
Number of lines IR
|
6
|
12
|
18
|
|
Number of lines R
|
6
|
12
|
18
|
Table 8.4
Internal vibrations of phosphate groups in calcium phosphates of interest (HPO4 2−-containing compounds)
|
Octacalcium phosphate (OCP); Ca8(PO4)4(HPO4)2, 5H2O; triclinic P−1 * HPO4 2− [14]
|
|||
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|
Site symmetry: C1
|
A(IR,R)
|
2A(IR, R)
|
3A(IR, R)
|
|
Factor group: Ci
|
4+2*Ag(IR)
|
8+4*Ag(IR)
|
12+6*Ag(IR)
|
|
4+2*Bu (R)
|
8+4*Bu(R)
|
12+6*Bu(R)
|
|
|
Number of lines IR
|
4+2*
|
8+4*
|
12+6*
|
|
Number of lines R
|
4+2*
|
8+4*
|
12+6*
|
|
Anhydrous dicalcium phosphate (DCPA) or monetite; CaHPO4; triclinic P−1
|
|||
|
Site symmetry: C1
|
A(IR, R)
|
2A(IR, R)
|
3A(IR, R)
|
|
Group factor: Ci
|
2Ag(R)
|
4Ag(R)
|
6Ag(R)
|
|
2Au(IR)
|
4Au(IR)
|
6Au(IR)
|
|
|
Number of lines IR
|
2
|
4
|
6
|
|
Number of lines R
|
2
|
4
|
6
|
|
Dicalcium phosphate dihydrate (DCPD) or brushite; CaHPO4; monoclinic Ia [5]
|
|||
|
Site symmetry: C1
|
A(IR-R)
|
2A(IR-R)
|
3A(IR-R)
|
|
Site symmetry: Cs
|
A′(IR-R)
|
A′(IR-R)
|
2A′(IR-R)
|
|
A″(IR-R)
|
A″(IR-R)
|
||
|
Factor group: Cs
|
A′(IR-R)
|
2A′(IR-R)
|
3A′(IR-R)
|
|
A″(IR-R)
|
2A″(IR-R)
|
3A″(IR-R)
|
|
|
Number of lines IR
|
2
|
4
|
6
|
|
Number of lines R
|
2
|
4
|
6
|
The factor group treatment provides a complete prediction of the vibrational levels of a crystal for both internal and external vibration modes. This approach takes into consideration the whole content of the unit cell, including the correlations between the vibrations of similar groups in a crystal that may interfere with each other in a confined environment. These considerations result in additional vibrational levels of molecules and molecular ions as shown in Tables 8.2, 8.3, and 8.4. The number of predicted lines may vary considerably according to the structure. For compounds containing HPO4 2−, OH− ions, and water molecules, line broadenings are observed related to hydrogen bonding. In addition, libration transitions, which have not been considered here, appear in addition to bending and stretching lines.
The factor group may lead to weak shifts so, when numerous lines are expected, individual components are hindered by line broadening and cannot be distinguished. Molecular group theory, site symmetry, and factor group treatments do not allow the prediction of spectra with their line positions and intensities.
This information can be provided by quantum chemistry calculations [15]. For mineral structures with disordered or partially occupied sites and for solid solutions, factor group theory is more difficult to apply. For amorphous structures like amorphous calcium phosphates, the spectra prediction may rely on the symmetry of basic structural units, Posner’s clusters (Table 8.5) [16], although the S6 symmetry of these clusters has been discussed and lower symmetry, C1 or C3, has been proposed depending on the environment [17].
Table 8.5
Vibrations of phosphate groups in amorphous calcium phosphate (ACP) assuming a S6 symmetry of the Posner’s clusters [16]
|
ν 1 PO4
|
ν 2 PO4
|
ν 3, ν 4 PO4
|
|
|---|---|---|---|
|
Symmetry S6
|
Au(IR), Eu(IR)
|
2Au(IR), 2Eu(IR)
|
3Au(IR), 3Eu(IR)
|
|
Ag(R), Eg(R)
|
2Ag(R), 2Eg(R)
|
3Ag(R), 3Eg(R)
|
|
|
Number of lines IR
|
2
|
4
|
6
|
|
Number of lines R
|
2
|
4
|
6
|
8.2.2 Spectra of Well-Defined Stoichiometric Calcium Phosphates
The FTIR and Raman spectra of the most important calcium phosphates are shown in Figs. 8.1 and 8.2. Line positions are reported in Tables 8.6 and 8.7. Very often for complex structures, the assignments are difficult to obtain due to the superimposition of elementary fundamental vibrations. Theoretical calculated spectra can, in principle, be obtained if the crystal structure is known, and a few reports have been published on this subject [15].
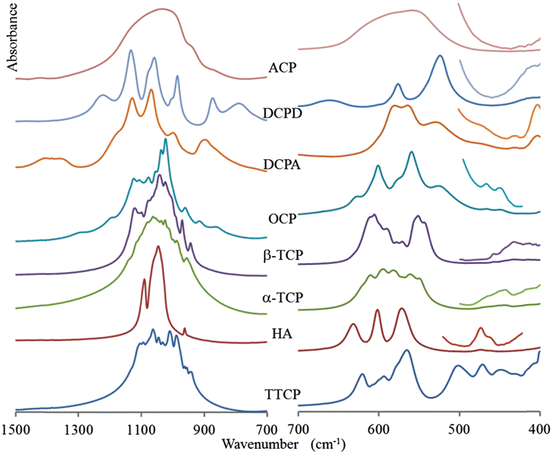
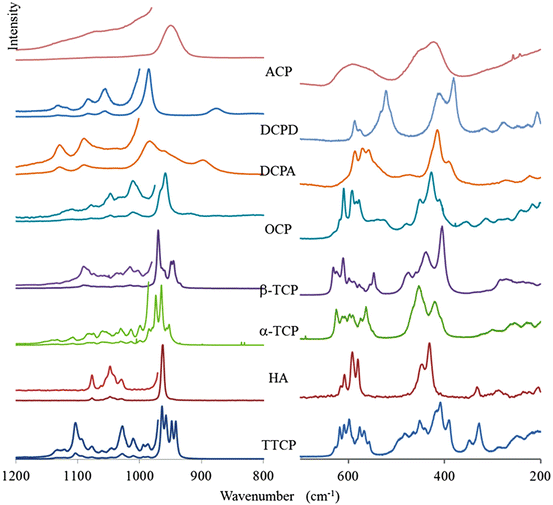

Fig. 8.1
FTIR spectra of calcium phosphates in the domains of internal vibrations of phosphate ions

Fig. 8.2
Raman spectra of calcium phosphates in the domains of internal vibrations of phosphate ions (for comparison purposes the wavenumber axis is in reverse order, like for the FTIR spectra)
Table 8.6
FTIR line positions of calcium phosphates (cm−1; m medium, s strong, sh shoulder, v very, w weak)
|
TTCP
|
HA
|
α-TCP
|
β-TCP
|
OCP
|
DCPA
|
DCPD
|
ACP
|
|
|---|---|---|---|---|---|---|---|---|
|
ν 3 PO4
|
1,400 w
|
|||||||
|
1,350 w
|
||||||||
|
1,295 w
|
1,215 m
|
|||||||
|
1,193 w
|
1,175 m,sh
|
|||||||
|
1,137 vvw
|
1,128 s
|
1,132 s
|
||||||
|
1,119 s
|
1,121 s
|
|||||||
|
1,105 w
|
1,103 s
|
|||||||
|
1,093 w
|
1,092 s
|
1,094 w,sh
|
||||||
|
1,073 w
|
1,080 w,sh
|
1,077 s
|
1,070 s
|
|||||
|
1,062 s
|
1,055 s
|
1,055 s
|
1,064 s
|
1,060 s
|
||||
|
1,046 s
|
1,040 vs
|
1,039 s
|
1,041 vs
|
1,040 s
|
||||
|
1,033 m
|
1,025 s
|
1,037 s
|
||||||
|
1,013 s
|
1,023 s
|
|||||||
|
1,010 s
|
997 s
|
1,010 w,sh
|
1,000 vvw
|
1,000 w,sh
|
||||
|
989 s
|
984 s
|
|||||||
|
ν 1 PO4
|
972 s
|
992 m
|
984 s
|
|||||
|
962 w
|
962 w
|
962 w
|
||||||
|
956 w
|
954 m
|
|||||||
|
946 w
|
945 m
|
949 w,sh
|
||||||
|
941 w
|
||||||||
|
P-OH of HPO4 2−
|
917 w
|
|||||||
|
861 w
|
892 m
|
872 m
|
||||||
|
ν 4 PO4
|
620 w
|
613 m
|
627 vw
|
|||||
|
594 w
|
601 m
|
597 m
|
602 m
|
601 m
|
||||
|
585 m
|
589 w
|
|||||||
|
571 s
|
575 m,sh
|
563 m
|
575 w
|
576 s
|
577 m
|
|||
|
561 m
|
551 m
|
550 m
|
560 m
|
563 s
|
560 m
|
|||
|
501 w
|
541 m
|
524 w
|
525 m
|
526 s
|
||||
|
ν 2 PO4
|
471 m
|
472 vw
|
471 w
|
480
|
||||
|
462 sh
|
463 w
|
466 vw
|
||||||
|
454 w
|
||||||||
|
450 w
|
430 w
|
432 vw
|
449 vw
|
428 vw
|
418 sh
|
|||
|
429 w
|
415 w
|
405 m
|
400 m
|
|||||
|
399 m
|
398 sh
|
|||||||
|
References
|
[10]
|
[12]
|
[13]
|
[12]
|
[14]
|
[12]
|
[18]
|
Table 8.7
Raman line positions of calcium phosphates (cm−1; m medium, s strong, sh shoulder, v very, w weak)
|
TTCP
|
HA
|
α-TCP
|
β-TCP
|
OCP
|
DCPA
|
DCPD
|
ACP
|
|
|---|---|---|---|---|---|---|---|---|
|
ν 3 PO4
|
1,131 m
|
1,132 vw
|
||||||
|
1,119 vw
|
1,119 vw
|
1,118 w
|
||||||
|
1,101 w
|
1,112 w
|
|||||||
|
1,091 sh
|
1,077 w
|
1,077 w
|
1,090 w
|
1,079 vw
|
1,094 m
|
1,079 w
|
||
|
1,076 vw
|
1,064 w
|
1,061 m
|
||||||
|
1,057 w
|
1,058 w
|
1,052 w
|
||||||
|
1,045 vw
|
1,048 w
|
1,048 w
|
1,050 w
|
|||||
|
1,041 w
|
||||||||
|
1,034 w
|
1,036 vw
|
|||||||
|
1,026 w
|
1,029 w
|
1,027 w
|
1,027 vw
|
|||||
|
1,008 w
|
1,012 w
|
1,015 w
|
1,011 m
|
|||||
|
998 w
|
1,005 w,sh
|
|||||||
|
ν 1 PO4
|
983 vw
|
976 s
|
||||||
|
961 vs
|
964 vs
|
964 s
|
970 s
|
966 s
|
988 s
|
986 s
|
||
|
956 vs
|
954 sh
|
948 s
|
959 vs
|
|||||
|
946 s
|
951 s
|
|||||||
|
940 s
|
||||||||
|
P-OH st. of HPO4 2−
|
916 w
|
900 m
|
||||||
|
874 w
|
878 m
|
|||||||
|
ν 4 PO4
|
615 vw
|
614 w
|
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


