Compound
Abbreviation
Chemical formula
Ca/P
logKsp
Monocalcium phosphate monohydrate
MCPM
Ca(H2PO4)2·H2O
0.5
Highly soluble
Monocalcium phosphate anhydrous
MCPA
Ca(H2PO4)2
0.5
Highly soluble
Dicalcium phosphate dihydrate
DCPD
CaHPO4·2H2O
1.0
6.59
Dicalcium phosphate anhydrous
DCPA
CaHPO4
1.0
6.90
Octacalcium phosphate
OCP
Ca8H2(PO4)6·5H2O
1.33
96.6
α-Tricalcium phosphate
α-TCP
Ca3(PO4)2
1.5
β-Tricalcium phosphate
β-TCP
Ca3(PO4)2
1.5
28.9
Hydroxyapatite
HAp
Ca10(PO4)6(OH)2
1.67
116.8
Tetracalcium phosphate
TTCP
Ca4(PO4)2O
2.0
38–44
Figure 7.1 shows the phase diagram of calcium phosphates in relation to CPC. Hydroxyapatite (HAp) is the most stable phase thermodynamically when the pH is approximately 4.2 or higher. However, brushite or dicalcium phosphate dihydrate (DCPD) becomes the most stable phase thermodynamically when the pH is approximately lower than 4.2. When the pH level drops to approximately 2, monocalcium phosphate monohydrate (MCPM: Ca(H2PO4)2·H2O) will become, in terms of thermodynamics, the most stable phase. It should be noted that apatite and brushite, final product of apatite cement and brushite cement, are the most stable phase thermodynamically at certain pH. Setting reaction of calcium phosphate cements is basically the same as the setting reaction of gypsum and is known as dissolution-precipitation reaction and entanglement of the precipitated crystals [10–16].
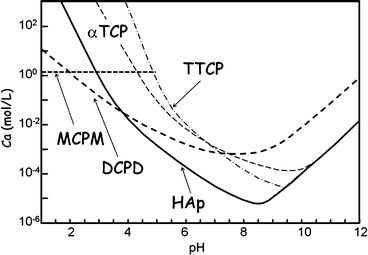

Fig. 7.1
Phase diagram of the solubility of several calcium phosphates as a function of pH. Solubility is expressed as the Ca concentration
Gypsum, calcium sulfate dihydrate (CaSO4·2H2O), and its dehydrated product calcium sulfate hemihydrate (CaSO4·0.5H2O) are known as gypsum plaster or plaster of Paris (POP). Calcium sulfate hemihydrate is produced by heating gypsum to approximately 150 °C. Although they have the same chemical composition except for the hydrated water, their solubility is different as shown in Fig. 7.2.
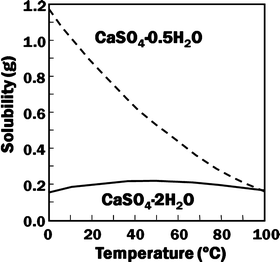

Fig. 7.2
Solubility of calcium sulfate hemihydrate and dihydrate as a function of temperature
For example, solubility of calcium sulfate hemihydrate is 0.9 g/100 mL at 20 °C. When calcium sulfate hemihydrate powder is mixed with water, it partially dissolves to supply calcium and sulfate ions which are equivalent to 0.9 g of calcium sulfate hemihydrate as shown in Eq. (7.1).
If calcium sulfate hemihydrate is the only chemical that could be in equilibrium with Ca2+ and SO4 2−, the solution will reach equilibrium with respect to the calcium sulfate hemihydrate, and no further reaction will occur. However, the solution will also achieve equilibrium with calcium sulfate dihydrate, and its solubility is 0.2 g/100 mL, which is smaller than the solubility of calcium sulfate hemihydrate which is 0.9 g/100 mL. Therefore, the solution is supersaturated with respect to calcium sulfate dihydrate. This results in the precipitation of calcium sulfate dihydrate crystals as shown in Eq. (7.2). The precipitation of calcium sulfate dihydrate leads to undersaturation of the solution. Therefore, calcium sulfate hemihydrate will further be dissolved in the solution. These reactions continue successively, and the precipitated calcium sulfate dihydrates entangle each other to set [16]:
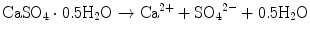
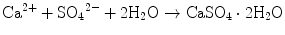
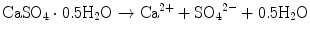
(7.1)
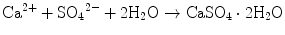
(7.2)
In the case of apatite cement also, setting reaction is the dissolution-precipitation reaction and entanglement of the precipitated apatite crystals [10–15]. For example, α-tricalcium phosphate (α-TCP) is known to form apatite upon setting [1]. α-Tricalcium phosphate is more soluble when compared with apatite as shown in Fig. 7.1. When α-tricalcium phosphate is mixed with water, it dissolves and supplies Ca2+ and PO4 3− into water as shown in Eq. (7.3). If α-tricalcium phosphate is the only chemical that could be in equilibrium with Ca2+ and PO4 3−, the solution would just be in equilibrium with respect to the α-tricalcium phosphate, and no further reaction would take place. However, the solution is also in a state of equilibrium with calcium-deficient hydroxyapatite, and its solubility is smaller than the solubility of α-tricalcium phosphate. Therefore, the solution is said to be supersaturated with respect to calcium-deficient hydroxyapatite. This results in the precipitation of calcium-deficient hydroxyapatite crystals as shown in Eq. (7.4). The precipitation of calcium-deficient hydroxyapatite results in undersaturation of the solution. Therefore, α-tricalcium phosphate will be dissolved in the solution. These reactions continue successively, and the precipitated calcium-deficient hydroxyapatite crystals entangle each other to set. The overall reaction can be expressed as shown in Eq. (7.5):
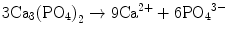
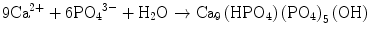
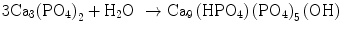
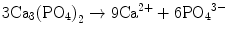
(7.3)
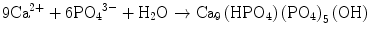
(7.4)
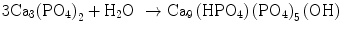
(7.5)
Apatite cement can be made with various chemicals that contain calcium and phosphate. For example, an equimolar mixture of tetracalcium phosphate (TTCP: Ca4(PO4)2O) and dicalcium phosphate anhydrous (DPCA: CaHPO4) is known as typical apatite cement [3–7]. Apatite cement should contain calcium and phosphate in its composition so that apatite can be produced. The components should have suitable solubility in water since the setting reaction of the apatite cement is a dissolution-precipitation reaction. The cement paste should show moderate pH so that apatite is the most stable phase thermodynamically at that pH since setting reaction of the apatite cement is the dissolution-precipitation reaction.
Figure 7.3 summarizes the SEM images of (a) set gypsum and (b) set apatite cement made of an equimolar mixture of TTCP and DCPA. Basically, they showed the similar structure. In other words, precipitated needlelike crystals entangled each other to form set mass.


Fig. 7.3
SEM images of the set apatite cement made of TTCP and DCPA and set gypsum
Brushite cement also sets in a similar setting reaction, dissolution-precipitation, and entanglement of precipitated crystal. The key difference of apatite cement and brushite cement is the final product. As stated earlier, brushite is the most stable phase when the pH is the approximately 2.0–4.2 (see Fig. 7.1). As a result, the components in brushite cement should contain calcium and phosphate that could form brushite, and the pH of the cement paste should be 2.0–4.2. One of the examples of the brushite cement is the mixture of β-tricalcium phosphate and monocalcium phosphate monohydrate. In this cement, monocalcium phosphate monohydrate shows relatively high solubility, and its dissolution results in acidic solution as shown in Eq. (7.6). Acidic solution results in the dissolution of β-tricalcium phosphate as shown in Eq. (7.7). The acidic solution in the cement paste containing Ca2+ and HPO4 2− will be supersaturated with respect to brushite. Therefore, brushite crystals are precipitated, and the precipitated brushite crystals entangle each other to set as shown in Eq. (7.8). The overall reaction can be expressed as shown in Eq. (7.9):
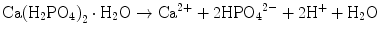
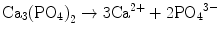
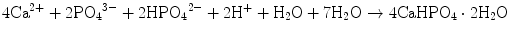
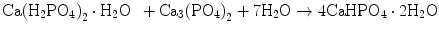
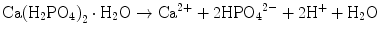
(7.6)
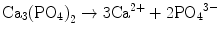
(7.7)
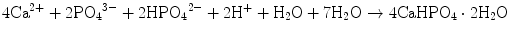
(7.8)
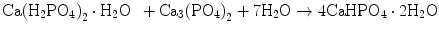
(7.9)
Before the invention of CPCs, acrylic cement was the only bone cement in use. Acrylic bone cement also consists of a powder and liquid phase. Powder phase contains polymethyl methacrylate (PMMA), and liquid phase contains methyl methacrylate (MMA). When the powders and liquids are mixed, radical polymerization will occur based on the reaction of methyl methacrylate contained in the liquid phase and the polymerization initiator contained in the powder phase. MMA will also dissolve in PMMA and increases the viscosity of the paste during the setting or polymerization process. In the case of setting reaction of acrylic cement, significant heat is generated due to radical polymerization. Heat generation is natural since PMMA is more stable thermodynamically than MMA. However, heat generation should be avoided for biomaterials since it could damage surrounding tissue. Also, unreacted MMA is not ideal to human tissues.
Gypsum plaster also generates heat upon setting reaction as shown in Eq. (7.10):
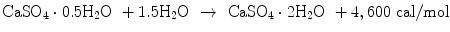
(7.10)
Fortunately, heat generation is negligible in the case of CPCs at least for tissue response. Of course, heat is generated based on the setting reaction since apatite or brushite is the most stable phase thermodynamically. Thus, setting reaction of CPCs can be monitored by thermal analysis. However, heat generation due to setting reaction of CPC is limited, and consequently there is no need to pay attention to the heat generation in the case of CPC. It should be noted that this is a big advantage of CPCs for clinical use. Negligible heat generation due to the setting reaction of CPC can be explained by the relatively slow setting reaction when compared to the acrylic cement rather than the small difference in enthalpy. In other words, one of the factors that govern the temperature of the cement is the result of balance of generated heat and diffused heat. Diffusion of the generated heat is enough to prevent acute temperature increase if setting reaction takes relatively long time.
Another problem for the acrylic bone cement is the unreacted monomer, methyl methacrylate (MMA). Basically, MMA is toxic to human tissue. Fortunately, unreacted component of calcium phosphate cement does not cause toxic effect. In fact, TTCP usually remains unreacted in set TTCP-DCPA-type apatite cement. Unreacted TTCP acts as a filler of the cement and causes no adverse effect to tissue response.
On the other hand, it should be emphasized that CPCs show excellent tissue response only when set. In the other words, CPCs cause inflammatory response when they failed to set. All calcium phosphate powders including apatite powders are known to cause inflammatory response called crystalline inflammatory response. Therefore, an assurance in the setting reaction is one of the key advantages for the successful clinical results when using CPCs.
7.3 Regulations in Setting Reaction
Obviously, the key factor for the usefulness of calcium phosphate cement is its self-setting ability. Bone defect can be reconstructed using calcium phosphate cement without having a gap between the bone defect surface and set calcium phosphate cement. That is one of the key reasons why calcium phosphate bone cement shows better bone formation when compared to apatite block or apatite granular. When bone defect is reconstructed with apatite block, it is impossible to place apatite block into the bone defect without a gap being generated between the apatite block and bone defect. In the case of apatite granular, the gap between the granular and existing bone can be minimized. However, granular cannot be fixed at the bone defect and could be fluctuated. In contrast to the reconstruction using block or granular apatite, apatite cement can fill the bone defect without having a gap against the surface of bone defect, and the set apatite cement can supply concrete apatite surface.
Although apatite cement shows better bone-forming ability when compared to apatite block or apatite granular, apatite cement can cause inflammatory response when it fails to set as mentioned earlier. It should be emphasized that powder in micron size elicits inflammatory response even its composition is hydroxyapatite. Similar response is observed when apatite cement failed to set. For example, apatite cement powder would be released when apatite cement paste was rubbed by the covering skin before its setting reaction. Also, apatite cement powder would be released from apatite cement paste when apatite cement paste is exposed to body fluid before its setting reaction.
Figure 7.4 shows the appearance of apatite cement paste when implanted subcutaneously in rat. In this condition, cement paste is exposed to some pressure from the covering skin. Fast-setting apatite cement (left) which sets in 5 min sets even at this condition due to the rapid development of mechanical strength [14]. In contrast, conventional apatite cement (cAC) which sets in 30–60 min could not withstand this pressure since the development of mechanical strength takes time. Therefore, cAC disintegrated at this condition. When apatite cement failed to set, it causes inflammatory response.
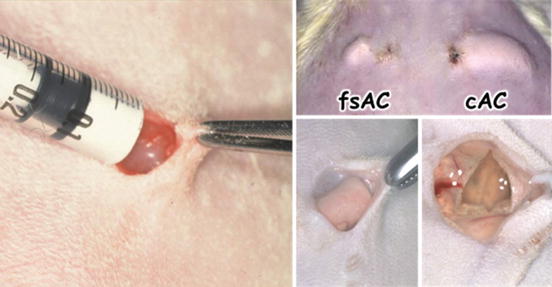

Fig. 7.4
Pictures of fast-setting apatite cement (fsAC) and conventional apatite cement (cAC) when the paste was implanted subcutaneously in rat
Therefore, regulation of the setting reaction of apatite cement is important not only for its handling properties but also for its tissue response. Since setting reaction of calcium phosphate cement is based on dissolution-precipitation reaction and entanglement of the precipitated calcium phosphate crystals, particle size has an influence on the setting reaction. In other words, larger powder has smaller specific surface area, and rate of dissolution is slow. This results in calcium phosphate cement with longer setting time. Regulating particle size is especially important in the case of calcium phosphate cement that consists of multiple calcium phosphates since the balanced supply of Ca2+ and PO4 3− based on the dissolution is important for the precipitation of the calcium phosphate.
In the case of apatite cement consisting of TTCP and DCPA, both TTCP and DCPA can supply Ca2+ and PO4 3− as shown in Eqs. (7.11) and (7.12). Then, Ca2+ and PO4 3− precipitated as hydroxyapatite crystals as shown in Eq. (7.13). The overall reaction can be expressed as shown in Eq. (7.14):
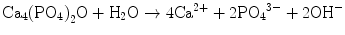
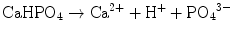
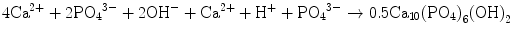
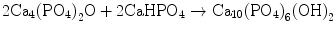
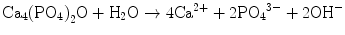
(7.11)
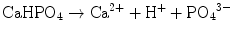
(7.12)
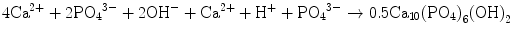
(7.13)
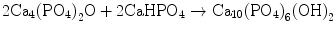
(7.14)
However, Ca/PO4 molar ratio supplied by TTCP and DCPA is different. TTCP which has Ca/PO4 ratio of 2.0 supplies larger amount of Ca2+ for the formation of HAp which has Ca/PO4 ratio of 1.67. In contrast, DCPA which has Ca/PO4 ratio of 1.0 supplies less amount of Ca2+ for the formation of HAp which has Ca/PO4 ratio of 1.67. Therefore, TTCP and DCPA should dissolve at the same rate for the formation of hydroxyapatite. Unfortunately, dissolution rate is different between TTCP and DCPA if the particle sizes are the same. TTCP dissolves much faster than DCPA as shown in Table 7.1.
Table 7.2 summarizes the effect of particle size on mechanical strength of TTCP-DCPA-type apatite cement consisting of equimolar mixture of TTCP and DCPA when mixed with distilled water. In this experiment, TTCP and DCPA with different particle sizes were used. Particle sizes were 12.4 and 1.6 μm for TTCP and 11.9 and 0.9 μm for DCPA. Apatite cement consisting of a mixture of small TTCP (1.6 μm) with large DCPA (11.9 μm) did not reach setting. Compressive strength of set apatite cement increases with particle size ratio of TTCP-DCPA. Rate of DCPA dissolution is slower when the particle size or the surface areas are the same. Therefore, smaller DCPA with large surface area need to be used for the simultaneous dissolution or simultaneous supply of Ca2+ and PO4 3−.
Table 7.2
Effects of particle size on the compressive strength of calcium phosphate cement consisting of tetracalcium phosphate and dicalcium phosphate anhydrous
|
Average particle diameter (μm)
|
|||
|---|---|---|---|
|
TTCP
|
DCPA
|
Ratio of the average particle diameter of TTCP/DCP
|
Compressive strength (MPa)
|
|
1.6
|
11.9
|
0.13
|
0 (no setting)
|
|
12.4
|
11.9
|
1.04
|
7.1 ± 1.0
|
|
1.6
|
0.9
|
1.78
|
21.8 ± 4.4
|
|
12.4
|
0.9
|
13.78
|
51.0 ± 4.5
|
TTCP-DCPA-type apatite cement initially supplied for clinical use requires a setting time of 30–60 min. Based on the information from the cement supplier, they confirmed the setting reaction and advised to use new cement if the old cement failed to set. Obviously, 30–60 min was too long for clinical use.
Figure 7.5 shows the Ca2+ and PO4 3− concentrations in the cement powder suspension using equimolar mixture of 12.4 μm TTCP and 0.9 μm DCPA. As shown in the figure, PO4 3− concentration decreases until it was no longer detectable after 30 min, whereas Ca2+ remains in the solution. This result indicated that PO4 3− supply is the rate-determining step for the precipitation of hydroxyapatite even for mixtures of large TTCP and small DCPA. As stated already, DCPA supplies more PO4 3− for the precipitation of hydroxyapatite when compared to TTCP. Therefore, DCPA dissolution is the critical step for the setting reaction of apatite cement.
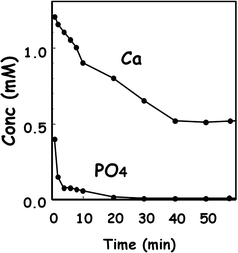

Fig. 7.5
Concentration of Ca2+ and PO4 3− in TTCP-DCPA suspension in distilled water
The results of chemical potential plot of cement powder suspension using equimolar mixture of 12.4 μm TTCP and 0.9 μm DCPA [12] are shown in Fig. 7.6. The figure reveals the solution is undersaturated with respect to HAp even though setting reaction of the apatite cement is a dissolution-precipitation reaction and entanglement of the precipitated apatite crystals. Therefore, precipitation reaction needs to be enhanced for quicker setting reaction.
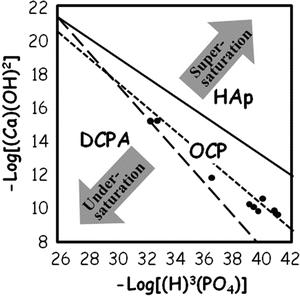

Fig. 7.6
Chemical potential plot of TTCP-DCPA in aqueous suspension
We can enhance the precipitation reaction by using seed crystals. Doi et al. have prepared HAp at different temperatures from 40 to 100 °C. Setting time of TTCP-DCPA-type apatite cement became shorter by adding the HAp seed crystal. Furthermore, the setting time was shortened when seed crystal was added to HAp prepared at low temperature but resulted in poor crystallinity [17, 18].
Ruslin reported the effects of placement of HAp seed crystal in α-TCP-based apatite cement [19]. When α-TCP was partially hydrolyzed, HAp was formed on the surface of α-TCP powder, and this powder was used as the cement powder. The conversion to HAp was faster when the same amount of HAp was introduced externally as shown in Fig. 7.7.
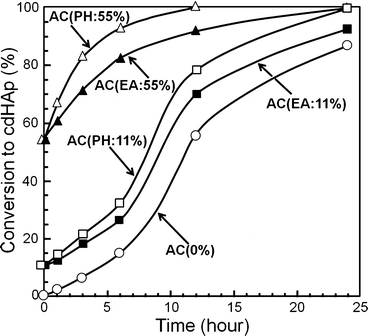

Fig. 7.7
Conversion of α-TCP-type apatite cement containing 0, 11, and 55 wt% seed HAp as a function of incubation time when kept at 37 °C and 100 % humidity
What’s more, when no HAp seed crystal or small amount of HAp seed crystal was introduced to apatite cement, conversion to HAp followed sigmoid curve which is typical for self-catalysis. Based on these observations, it was revealed that HAp shows seeding effect and its effect is more remarkable when HAp seed crystals were located on the surface of α-TCP powder. As shown in Eq. (7.3), α-TCP dissolves to supply Ca2+ and PO4 3−. Then, Ca2+ and PO4 3− will be supersaturated with respect to calcium-deficient apatite and precipitated as calcium-deficient apatite. When HAp seed crystal was located on the surface of α-TCP powder, dissolved Ca2+ and PO4 3− from α-TCP is thought to be used immediately to grow HAp seed crystals.
Although the addition of HAp seed crystal was effective to shorten the setting time, unfortunately the mechanical strength of the set apatite cement was decreased. The reduction in mechanical strength is thought to be the result of more frequent nuclei and limiting crystal growth. The decrease in mechanical strength of set apatite cement can be minimized by placing seed HAp on the surface of α-TCP powder by partial hydrolysis as shown in Fig. 7.8. Mechanical strength of the set apatite cement was closely related with the entanglement of precipitated HAp crystals. When HAp crystals were located on the surface of α-TCP, HAp crystals became longer, and interlocking reaction can be expected at higher density.
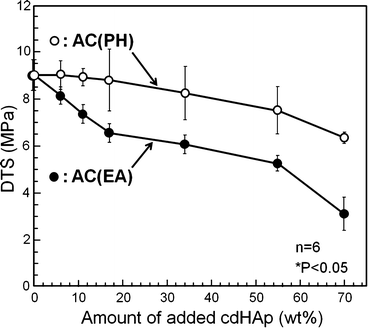

Fig. 7.8
Effects of placement of seed HAp on diametral tensile strength of α-TCP-type apatite cement. PH: HAp seed crystal was located on the surface of α-TCP by partial hydrolysis. EA: HAp seed crystal was externally added
A more effective method to increase the setting reaction or the enhancement of apatite formation is the addition of PO4 3− into the liquid phase of cement. As shown in Figs. 7.5 and 7.6, liquid portion of TTCP-DCPA paste is undersaturated with respect to HAp if TTCP-DCPA is mixed with water due to the limited supply of PO4 3− based on the dissolution of DCPA.
Moreover, the addition of the PO4 3− into the liquid phase could result in the immediate supersaturation of HAp and causes an immediate HAp formation upon dissolution of TTCP, which plays a more predominant role in the supply of Ca2+. Consequently, the setting time of the apatite cement should be shortened.
Table 7.3 summarizes the effect of liquid phase on setting time of TTCP-DCPA-type apatite cement. Setting time of this apatite cement was 30 min when distilled water was used as the liquid phase. In contrast, setting time became 5 min when phosphate salts were used as the liquid phase [12, 14]. Basically, no effect was found on the type and concentration of phosphate salt employed in the experiment.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


