In Part 1 of this series of articles on growth-curve modeling, we demonstrated how to use multilevel curvilinear models to analyze longitudinal orthodontic growth data. In Part 2, we demonstrated that nonlinear growth curves provide an alternative approach to individual growth curve fitting. In this article, Part 3 of the series, we shall demonstrate how to fit nonlinear growth curves to a group of subjects within the framework of multilevel modeling and compare its results with multilevel curvilinear modeling with higher polynomial terms. All our analyses were undertaken using the library nlme for the free statistical software R (version 2.15.3; R Core Team, 2013, Vienna, Austria).
We obtained data for 8 girls and 15 boys for whom serial cephalometric tracings were undertaken between the ages of 4 and 22 years from the archives at the American Association of Orthodontists Foundation Craniofacial Growth Legacy Collection. Each subject had 9 to 17 cephalometric tracings. In this article, the outcome of our nonlinear modeling was the growth in total face height.
Statistical analysis
We first plotted the observed total face height for the 23 subjects to examine the growth patterns. Figure 1 shows the observed total face height growth curves for each subject separately, and it became apparent that the cephalometric tracings for total face height contained measurement errors because for some subjects, total face height measured at later ages was smaller than previously. For our demonstration, the 23 subjects were selected because of 2 important features in their observed growth curves. First, the acceleration in growth velocity for total face height started at adolescence, although the ages when this acceleration started and the magnitude of acceleration varied among them. Second, at the end of the observation, growth in total face height seemed to reach maturity, although there were substantial differences in the timing and the final adult total face height. Ideally, we would therefore like our growth models to not only characterize those growth features but also provide estimates for key attributes of the growth process: eg, average growth velocity, age with the greatest growth velocity, and final adult total face height.
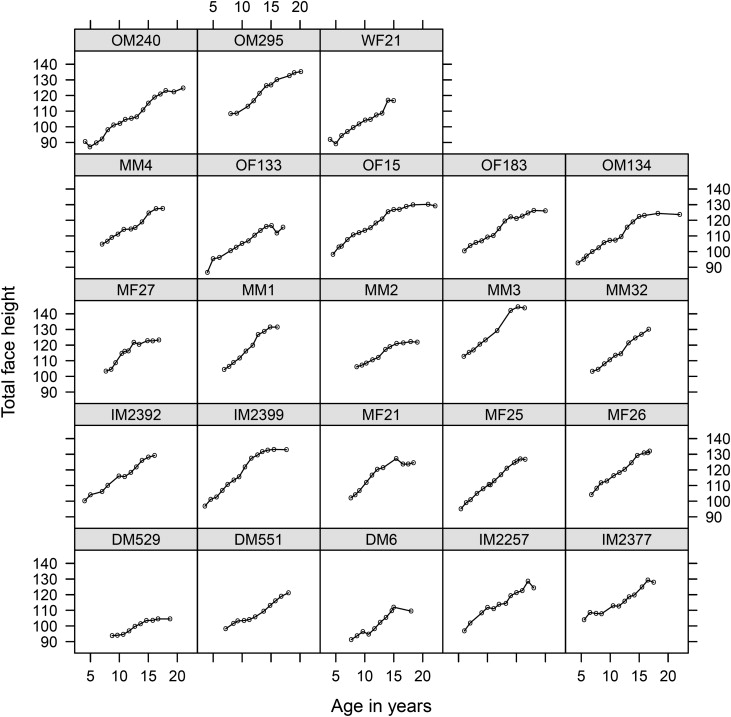
Figure 1 suggests that a sigmoid function might be required to capture the growth features, such as growth spurt, average growth velocity, and final total face height. In our previous article, the multilevel Preece-Baines model was shown to be a good candidate for such a task, and the model can be written as follows.
T F H = h 1 + 2 ( h 1 − h θ ) e s 0 ( A g e − θ ) + e s 1 ( A g e − θ )
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


