Introduction
The purpose of this research is to determine the accuracy and reliability of measurements obtained from 3-dimensional (3D) cone-beam computed tomography (CBCT) for different head orientations.
Methods
Stainless steel wires were fixed to a dry skull at different places. The skull was scanned by using CBCT in the centered and 5 other positions. Intraobserver and interobserver reliability tests were performed by using 6 landmarks identified on the virtual 3D skulls by 2 operators. Two methods were used to determine the accuracy of measurements on the virtual 3D skull scanned in different positions. In the first method, 12 linear distances were compared on the physical skull and the 3D virtual skull in the centered and the other scanning positions. In the second method, registration of each of the 5 positions on the centered position was done separately, and coordinates of 11 landmarks were identified in each position and compared with the centered position. Data gathered from the 2 methods were compared statistically.
Results
Concordance correlation and Pearson correlation coefficients values were almost 0.9999 in all the comparisons denoting: (1) high intraobserver and interobserver reliability; (2) very high concordance between the physical skull and the CBCT centered-position measurements; (3) very high concordance between measurements of the centered position in relation to those obtained from the different skull positions; and (4) registration of the skulls in the different positions showed high concordance, with the highest values between the centered and off-centered positions, and the lowest with the complex position.
Conclusions
Accuracy and reliability of CBCT measurements are not affected by changing the skull orientation. Thus, the upper-lip and chin rests should not be considered absolute requirements during CBCT imaging if a stable head position is ensured.
Interest in 3-dimensional (3D) imaging devices has grown over the last decade. Orthodontists are beginning to appreciate the advantages of the third dimension in clinical diagnosis, treatment planning, and patient education. Cone-beam computed tomography (CBCT) is being more frequently applied for orthodontic assessment. CBCT provides immediate and accurate 2-dimensional and 3D radiographic images of an anatomic structure, limited only by the system’s innate or selected field of view. For machines with large fields of view (eg, the Galileos CBCT machine; Sirona, Bensheim, Germany), the data acquired by the scan can be used to reconstruct approximations of 2-dimensional cephalograms and also for a growing number of 3D analyses. CBCT has been used now for several years. Its applications in dentistry have already been determined by its performance, low cost, and low radiation dose. However, accuracy for various uses has not yet been verified.
Recent studies have shown some controversies concerning the accuracy of the measurements obtained from CBCT. Lascala et al found that, although the CBCT image underestimated the real distances between skull sites, the differences were significant only for the skull base; therefore, it was reliable for linear evaluation measurements of other structures more closely associated with dental and maxillofacial imaging.
On the other hand, Lagravere et al evaluated the accuracy of measurements made on 9-in and 12-in CBCT images compared with measurements made on a coordinate measuring machine; they found no significant statistical differences between the linear and angular measurements from the coordinate measuring machine and the NewTom 3G (Aperio Services, Verona, Italy) images. Hence, they concluded that the NewTom 3G produces a 1-to-1 image-to-reality ratio.
In another study, Periago et al compared the reliability and accuracy of linear measurements made on 3D volumetric reconstructions generated from CBCT data sets to direct measurements made on ex-vivo skulls. They found that, for two thirds of the dimensions, the CBCT measurements were statistically significantly different from the actual measurements. However, they commented that, after analyzing the absolute and percentage differences, this statistical significance probably did not translate into clinical relevance.
Recently, 2 studies investigated the effects of changing the position of the head in the CBCT machine on the accuracy of the measurements obtained. In the study by Hassan et al, 8 dry skulls were scanned twice with the NewTom 3G CBCT in ideal and rotated positions. The findings indicated that measurements based on 3D CBCT surface images were accurate, and small variations in the patient’s head position did not influence measurement accuracy. In the same context, Berco et al investigated the accuracy and reliability of CBCT measurements compared with the true measurements of a dry skull in 2 orientations: with the Frankfort horizontal plane parallel to the floor, and with the Frankfort horizontal plane aligned 45° to the floor. No statistically significant differences were observed between the measurements.
Although several attempts were made to verify the accuracy of CBCT, the verdict is not conclusive. In addition, the accuracy with respect to the orientation of the patient’s head without head-positioning devices is still an issue of concern.
CBCT machines have integrated head-positioning devices, such as the upper lip rest and the chin rest. Despite their importance to ensure stabilization as recommended by the manufacturers, they cause obliteration and distortion of the patient’s facial soft tissues ( Fig 1 ). The importance of visualization of the tissues of the lower third of the face in orthodontics should not be ignored. Thus, the aim of this study was to investigate the accuracy and reliability of CBCT measurements of various head orientations without upper-lip and chin rests.
Material and methods
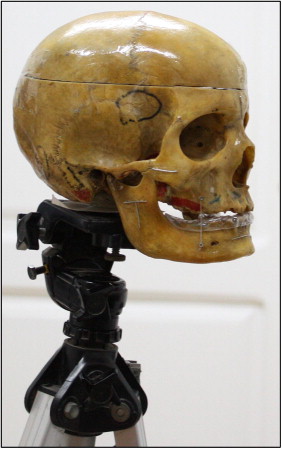
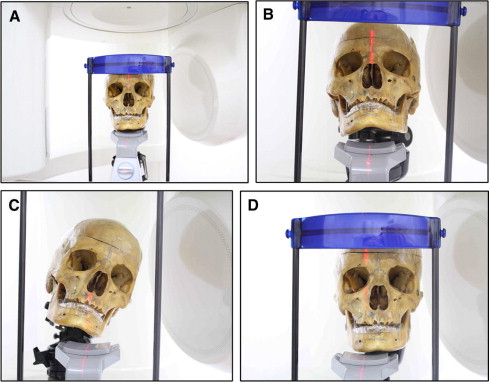
A dry skull was fixed on a tripod with a plumber mixture, which hardens 10 minutes after mixing the base and the catalyst. A stainless steel orthodontic wire, 0.7 mm in diameter, was cut into various lengths, arranged in 3 forms (horizontal, vertical, and T-shaped), and fixed bilaterally on the skull with permanent glue ( Fig 2 ). The skull was then scanned by using the Galileos CBCT machine with a standard scanning program (85 kV, 21 mA, 200 slices) in 6 positions without lip and chin rests: position 1 (centered), the skull was centered in the focal trough according to the manufacturer’s instructions ( Fig 3 , A ); position 2 (posterior tilt), the skull was tilted posteriorly from the centered position ( Fig 3 , B ); position 3 (lateral tilt), the skull was tilted laterally to the right of the observer; position 4 (torsion), the skull was rotated in a torsion pattern (rotation to the left of the observer around its long axis, which passes through the foramen magnum); position 5 (complex), the skull was tilted in a complex manner (combination of anteroposterior, lateral, and torsion movements) ( Fig 3 , C ); and position 6 (off centered), the skull in the centered orientation (position 1) was moved to the right of the observer ( Fig 3 , D ).
To calculate the changes in the skull position from position 1, first the skull in the centered orientation was altered to produce positions 2 through 6. Then the software calculated the precise amounts of spatial movement for the 5 positions (positions 2-6) ( Table I ).
| x | y | z | |
|---|---|---|---|
| Anteroposterior | |||
| Translation (mm) | 1.40169 | −6.98926 | 17.575 |
| Rotation (°) | −16.6091 | −0.55455 | −1.91792 |
| Lateral | |||
| Translation (mm) | −20.3651 | 14.3071 | 15.8192 |
| Rotation (°) | 10.576 | 18.6867 | 1.30573 |
| Torsion | |||
| Translation (mm) | −26.1911 | 33.6892 | 11.871 |
| Rotation (°) | 0.774023 | 3.17285 | −21.304 |
| Complex | |||
| Translation (mm) | 3.46304 | −15.4782 | 38.8496 |
| Rotation (°) | −11.1493 | 20.8478 | 20.704 |
| Off-centered | |||
| Translation (mm) | 16.9756 | 1.97839 | −1.76982 |
| Rotation (°) | −1.00116 | −0.03873 | 1.69138 |
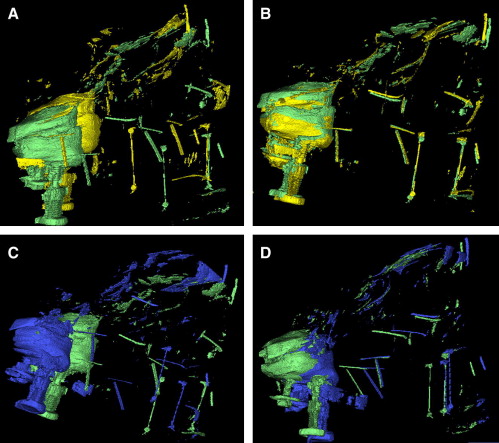
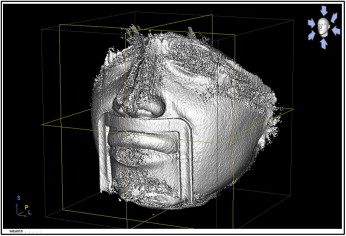
The 3D volumes of the virtual skulls were generated by compiling the computed tomography slices of the different skull positions by using the Mimics software (version 8.1; Materialise, Leuven, Belgium; Fig 4 ). The threshold of the 3D volume was adjusted to subtract the bone and visualize the wires glued on the skull ( Fig 5 ). The minimum and maximum thresholds were 2250 and 3071 Hounsfield units, respectively, which were applied to the 6 skull views.
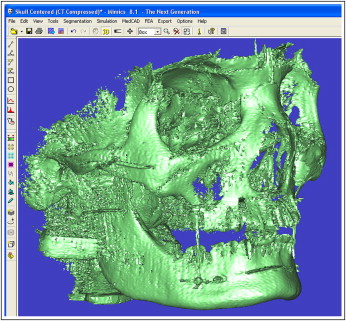

The intraobserver and interobserver reliability tests were performed to investigate the errors in the measurement method used in this study. Six well-defined landmarks (x, y, and z coordinates) were identified on the ends of the metal wires glued on the skull on each of the 6 skull views. Using the 3D visualization software, the landmarks were identified by an operator (A.R.E.-B.) and again 2 weeks later. The coordinates of the landmarks were recorded and compared to determine the intraobserver error. The same landmarks were identified by another operator (M.S.F.) and the coordinates compared with those of the first operator to investigate the interobserver error.
The life-sized output of the CBCT was investigated. The measurements of the wire lengths on the centered virtual skull position ( Fig 6 ) were compared with the true (physical) lengths of the wires glued on the skull (gold standard).
The null hypothesis of this study was that there is no difference in the output of the CBCT measurements when imaging the skull in the different orientations. Investigation of the null hypothesis was carried out using 2 methods; the first by comparing 12 linear distances between the same landmarks on the 6 virtual skulls. The second through registering (3D superimposition) each virtual skull (positions 2-5) on the centered virtual skull (position 1). This is done by assigning 3 well-defined points on the centered virtual skull position and locating 3 identical points on each of the other virtual skulls. Registration of each pair of virtual skulls on these 3 identical landmarks was thus performed.
The registration method used was based on a technique known as iterative closest point. The iterative closest point algorithm is a standard solution to the alignment problem of free-form surfaces. Its popularity can be accredited to its versatility; it can be used for point sets, implicitly and explicitly defined curves and surfaces, line segment sets (polylines), triangle sets (faceted surfaces), and volumes. This technique is characterized by high computational speed and ease of implementation. Also, it was proved to converge monotonically to the nearest local minimum of a mean-square distance metric. This method handles the full 6 degrees of freedom of rotation and translation.
This iterative algorithm has 3 basic steps: (1) pair each point of the first object to the closest point in the second object, (2) compute the transformation that minimizes the mean square error between the paired points with respect to the 6 rotations and translation parameters, and (3) apply the transformation to data-set points of the first object and update the mean square error.
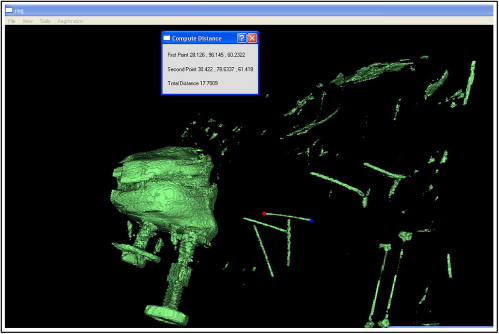
Afterward, coordinates of the 11 landmarks identified on each pair of registered skulls were compared. Any discrepancy between the coordinates would reflect distortion of the CBCT output with variable skull orientations ( Figs 7 , A and B , and 8 ).