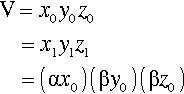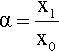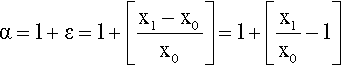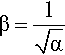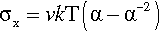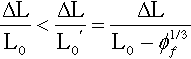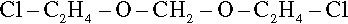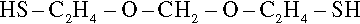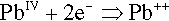Since many of the restorative devices that are used in dental treatment need to be fabricated outside of the mouth, ranging from inlays to full dentures, there are obvious problems in getting them to fit if reliance is placed on trial and error methods. This used to be done when full dentures were carved from materials such as ivory, but it was quickly realized that a model of the mouth made the task much easier. The problem then is one of making the model. For the model to be made, leaving aside the question of from what, a mould is required. The earliest mould material was in fact wax, soft enough that the shape of the teeth could be impressed into it, hence the term impression, even though very little pressure is used with most modern materials.

§1 Basic Requirements

The most important characteristic for an impression material is fairly obvious: it must accurately reproduce the entire surface upon which the device to be made will fit. All angles and distances must be preserved. This means that both small scale detail and larger scale dimensional accuracy must be attained, and particularly over the full size of the region being reproduced, in other words: no distortion. This requirement is more critical for larger devices. For example, an error of 10% when a 1 mm distance is considered may not seem very much, but clearly over 100 mm such an error would be laughable – more than the width of a tooth.

The second required characteristic is that of elasticity, in conjunction with a low elastic modulus and large elastic range (1§2.1). The reasons for this combination of properties are entirely due to the usual morphology of oral structures. Human teeth are not smoothly conical, but ‘waisted’. The cervix of the tooth is narrower in at least one direction than the crown, that is, there are ‘undercuts’. Thus, in order to remove an impression from an undercut it must be deformed, stretched, to allow the crown of the tooth to be slid out. This must only be a temporary deformation, so that the original dimensions are recovered perfectly, but with the least convenient force being used to avoid pain for, or injury to, the patient. The principal material requirement in this respect is its permanent deformation after stress, as shown, for example, by the compression set test (4§8). The implication here is that the impression should be removed in one ‘snap’, a quick operation that does not allow time for flow.

It will be found that these requirements cannot be met fully in practical materials, and to some extent are mutually incompatible. We have to find a workable compromise between these properties. The elastic modulus and flexibility requirements can be dropped for certain special applications, in particular for whole mouth edentulous impressions (assuming no undercuts in the bone-mucosa structure), when other properties assume dominance. Wax- and gypsum-based impression materials, used in these special cases, will not be dealt with in this chapter.

There are other considerations. Whatever process is used to create the elastic mould, time is an important factor: patient tolerance is limited, and a busy practice is said not to be able to afford the economic implications of disproportionately lengthy procedures. Whether this last item is a legitimate consideration needs to be judged in terms of the alternative: what is the most favourable course from the point of view of patient care? The toxicity of materials is of concern where soft-tissue contact occurs, and excessive heat must be avoided. Once a mould has been made, its useful life (duration, number of models that can be made) constrains its handling severely. Even colour has been found to be important: inspection by the clinician to determine the adequacy or otherwise of fine detail reproduction is limited by the opacity and contrast of the material. Given that a compromise is involved anyway, the cost of the material must be balanced against the benefit – the clinical outcome, which usually means asking whether the device being made ultimately fits well enough to be able to serve its clinical function indefinitely, assuming no other factors are operating.

§2 Deformation

The flexibility requirement arises essentially only because oral structures are undercut: a rigid impression could not be removed without cutting or breaking it. This can prove to be extremely difficult and distressing. A patient’s mouth will be fairly filled by the impression material and tray (which is often metal) and access for cutting tools is very limited and hazardous. Yet even if the material is deformable, the elastic modulus must not be so high that the load required to get the impression off the tooth exceeds that required to extract the tooth – or come anywhere near that value. It is obvious that an impression ought to be perfectly elastic to be withdrawn over such undercuts and then recover exactly the original shape. Equally obviously, it will not matter if the deformation is not Hookean, that is, proportional to stress, so the proportional limit of these materials is of no practical concern. In fact, the deviation from ideal behaviour in this sense can be very great without the slightest influence on the acceptability of the material. Conversely, the yield point is very important: no plastic deformation is, in principle, acceptable in the solid material.

It will be recalled that polymers are, as a general rule, characterized by their glass transition temperature, above which they exhibit rubbery behaviour (Fig. 3§4.13). To summarize what constitutes such a rubbery or elastomeric material, we may cite:

• free rotation of bonds,

• amorphous structure (i.e. not crystallize readily),

• cross-linking of chains to prevent relative slippage, and

• lack of interaction between chains.

Because of these structural factors, the mechanical behaviour of elastomers is characterized by two properties. Firstly, isotropic deformation; the lack of long-range structural regularity means that all directions in the mass are equivalent (at least, until appreciable deformation and therefore chain alignment has occurred). Secondly, deformation is at constant volume¹ (assuming constant temperature).structure and allowing chain segments to move freely. Some unusual polymers ha The freedom of chain segments to move means that the free volume (and thus average distance between chains) is hardly affected.

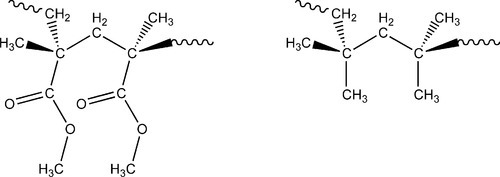
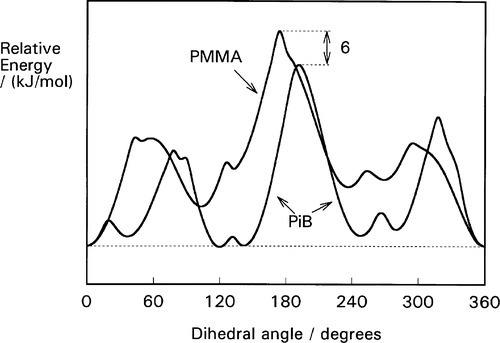
Thus, polyisobutylene (Fig. 2.1), for example, is a much better elastomer than poly(methyl methacrylate) (above its T_g, and thus in a rubbery state) because, despite the bulky methyl groups, chain segment rotation is easier by some 6 kJ/mol (Fig. 2.2). The ‘smoother’ chain of polyisobutylene (Fig. 2.3) also permits chain segment rotation and reptation more easily than does the more ‘knobbly’ PMMA (Fig. 2.4) because steric interaction between chains is less. Furthermore, being non-polar, the bonding between chains is only of the very weak van der Waals type (10§3), while the dipole on the carbonyl group of the PMMA strengthens inter- and intra-chain bonding.

In contrast to the above structurally-based explanation of an elastomer, we may also consider a more operational view, even though the structural reasoning is the same. Hence, we may define an elastomer as a three-dimensional network polymer which has been designed to have both good elasticity (in terms of its perfection) and have a large elastic range (1§2.1). Implicit in this is the assumption of being within an intended working range of temperature. Thus, T > T_g is required for it to be in the rubbery region (3§4.13), while clearly oxidation or decomposition sets an absolute upper limit to the working temperature range (it is clear that if the polymer is sufficiently cross-linked to be a good rubber, it will not have a meaningful melting or ‘rubbery flow’ point). We should also bear in mind that there will be strain-rate effects on the rubbery plateau as well (Fig. 3§6.2).

•2.1 Equations

Using a slightly different notation to that used in 1§2, we can express the constancy of volume in a simple equation. Thus, under uniaxial strain (in the x-axis), in tension or compression,

< ?xml:namespace prefix = "mml" ns = "http://www.w3.org/1998/Math/MathML" />V=x0y0z0=x1y1z1=αx0(βy0)(βz0)

where the subscript 0 refers to the original dimensions, and subscript 1 the dimensions after deformation; α and β are therefore the factors by which the original dimensions are changed, e.g.

α=x1x0

This α is termed the extension ratio,² and it is more usual to refer to that than strain in the context of elastomers because these materials usually have low elastic moduli and therefore show large values of strain at low stresses. Extension ratio and strain, ε are, however, simply related:

α=1+ε=1+x1−x0x0=1+x1x0−1

If α is measured, the lateral extension ratio, β, is easily found from equation 2.1:

β=1α

as clearly we must have αβ² = 1. The mobility of chain segments is sufficient to allow the rapid relief of lateral stresses, limited only by the relaxation time for the diffusion of chain segments. The Poisson ratio is therefore taken to be exactly one half, at least at low values of strain. Amongst the consequences of this is the impossibility of calculating the true modulus of elasticity or the bulk modulus from Young’s Modulus and the conventional formulae (equations 1§2.10, 1§2.23) since the divisor would become zero. This underlines the fact that there are always approximations in such calculations, i.e. dropping non-negligible higher powers of strain is not appropriate in these circumstances.

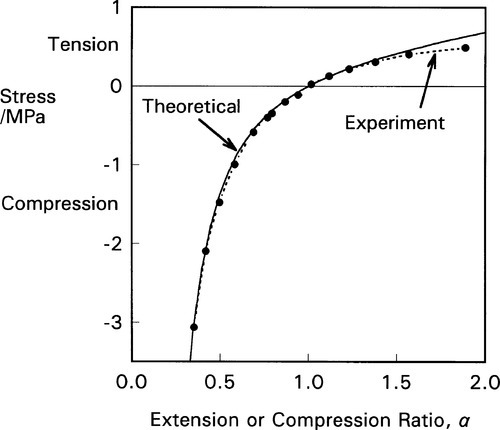
An equation relating the axial stress (σ_x) to the extension ratio in elastomers has been derived:

σx=vkTα−α−2

The constant of proportionality involves the absolute temperature, T, the Boltzmann constant, k, and v the number of effective chain segments per unit volume of the polymer. A segment can be considered as that length of polymer chain whose ends are more or less immobile (on the time scale of the observation) because of entanglement, branches or cross-links (3§3, 3§6.2). This equation has been shown to hold over a wide range of compression and extension (Fig. 2.5), although deviations start to appear at very high extensions. This illustrates the importance of the effect of polymer structure on the properties, and further permits the deliberate design of polymers with specific values for those properties. However, it is obvious that the stress-strain curve is nowhere linear. For this class of materials an approach to proportional extension may only be seen at very small stresses. We can see that they are not Hookean materials because the deformation internally is a rearrangement of chain segments and not the straining of primary interatomic bonds. The mechanism of deformation is therefore fundamentally different from that of most other types of material.

•2.2 Failure

During such deformation, the rearrangement of the polymers chains is such as to tend to align them. This is equivalent to drawing (3§4.7) except that macroscopic plastic strain – flow – is not required. Indeed, this is deliberately meant not to happen by the provision of cross-linking, and enhanced by the inevitable entanglements present.

These cross-links and entanglements are the defining feature of elastomers, preventing macroscopic chain drawing, because they are the source of the desired elasticity. However, once a section of chain has become straightened, the cross-link and entanglement points, as well as the length of chain between, must from now on carry proportionately more load than adjacent chains. That chain is taut, while the adjacent chains are carrying relatively little load (Fig. 2.6). The energy of deformation is now stored in bond length and angle strain. The (tangent) modulus of elasticity now tends to start to rise again (cf. Fig. 3§4.11). But if the load on any one bond in the chain exceeds its strength that bond must break. Such broken chains can then no longer contribute to the stiffness of the body in the region of the break. In other words, applying a sufficient stress to the body must result in some chains being broken even if no obvious plastic deformation or failure occurs, and this causes a reduction in elastic modulus. This is strain-softening.

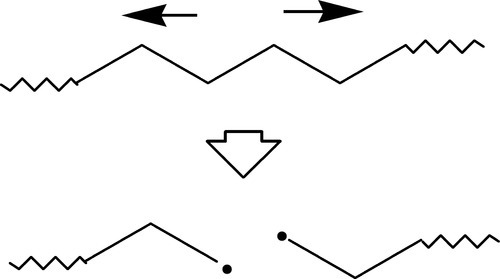
There are further consequences. The rupture of a polymer molecule commonly results in the formation of a pair of free radicals³ (homolytic scission) (Fig. 2.7). These radicals are active and high-energy entities which may take part in a number of further reactions. One of these is chain transfer (see 5§1.4). Ordinarily, this would not be a problem, but when the polymer is under stress further damage can be done. Thus, if the bond that the free radical attacks is under load, the rupture is easier (because of the stored energy) and leads to stress relaxation as the newly-formed radical-bearing chain end is pulled away (Fig. 2.8). This then throws the load onto adjacent chains. As they in turn become taut through localized drawing so they will become subject to attack by the new radical. The process can then be repeated indefinitely, or at least until another free radical is encountered and they mutually annihilate (cf. 5§1.3). In this way the nuclei of cracks will have been generated, and these will grow as the damage accumulates, in effect being sub-critical cracks in the Griffith sense (1§7). When they have grown to a critical size, then crack growth will initiate leading to spontaneous collapse.

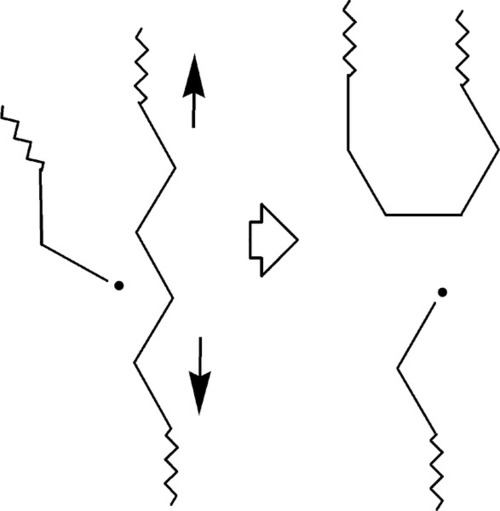
Even if the attacked chain is not under stress, entropic recoil means that the new chain end will tend to move away from its original position. Thus, the extra freedom that the chain end has, in the context of thermally-activated diffusion, means that the number of random coil conformations available has increased. An extended chain is relatively improbable, so recoil is expected, and would enhance the effect of stress relaxation.

There is one further aspect of this, which applies to many polymers under stress, not just elastomers: autocatalytic damage. When there is oxygen present (which in dental contexts cannot be avoided) this may react with the scission free radical. Reactions of the same type as occur with oxygen inhibition then can occur (6§6), the key feature being the multiplication of the numbers of radicals when the hydroperoxide formed itself undergoes homolytic scission spontaneously (reaction 6§6.3). This is perhaps a fairly slow process under most ordinary conditions, but it does account for the inability of many polymers to sustain tensile loads for extended periods and beyond the effects of simple diffusive creep.

As a further consequence of this kind of chemistry, we can note that PMMA and other free-radical polymerization systems are essentially equilibria. The “unzipping” process generates free radicals spontaneously. Clearly, these also permit stress-relaxation in the same way: even a small stress, below the strength of the bond, would result in chain-end separation, even if entropic recoil did not achieve this. Such a mechanism may be part of the creep process in filled-resin restorative materials (6§1.4).

•2.3 Cause of elasticity

It should perhaps be emphasised why elastomers are indeed rubbery, what gives them their elastic behaviour. Given that the natural state of a non-crystallizing polymer chain is an amorphous, random coil (Fig. 3§2.3), which represents the most probable state, this is maximum entropy – disorder. Work has to be done to straighten such chains (Fig. 3§2.4), raising the energy of the system. Since crystallization is not available as a path for lowering the energy, the stress is maintained by the sideways thermal motions of chain segments. Assuming that there are no other mechanisms operating to reduce that stress (such as chain ruptures), it will be maintained indefinitely at a constant temperature, indeed, the force generated will be a measure of temperature. If the constraint is removed, randomization again occurs through the rapid diffusion of chain segments to restore random coils everywhere. This is entropic recoil. It is clear that the speed of this is much lower than for bond length or angle strain, and indeed is a retarded recovery (4§5) as it is time-dependant. Note that the effect of a small sideways force requires a large resultant axial force to maintain the length: any displacement sideways must shorten the distance between the ends if the chain is not stretchy (Fig. 2.9).

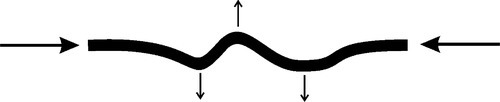
An experiment may be done to illustrate this (Fig. 2.10). Take a thick elastic band, and keeping it slack touch it to your lip to gauge the temperature. Stretch it quickly as far and as fast as you can, and again touch it to your lip: it is now warm from the work done. Keeping it stretched, wave it about in the air for a few seconds to cool again. Touch it to your lip to confirm this, then let it relax quickly and again touch to your lip: it is now cold because energy was required to re-establish the high entropy of the random coils. An analogy is melting – a disordered state created from an ordered one with the input of the latent heat of melting. The (relatively) ordered condition of the polymer chains when drawn requires the “latent heat” of randomization; this is taken from the material itself and the surroundings, hence the cooling. Equivalently, the warming on stretching is like the evolution of the latent heat of crystallization.

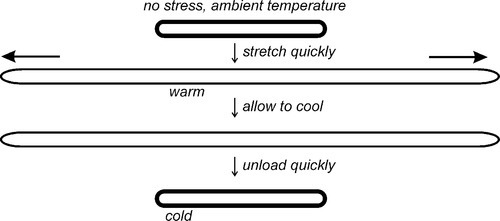
A second experiment might be to stretch such a band in the same way (but not with your fingers!) and immerse it while stretched in liquid nitrogen (77 K, –196 °C), converting it to a hard glass (for natural rubber, T_g ~ –65 °C; 27§1). It is now rigid, and retains its length when let go as there is no chain segment diffusion. There is no restoring force. Allow it to warm up and recovery becomes rapid when the temperature of the rubber rises above its T_g. A similar effect can be seen when a drawn polymer filament, such as nylon fishing line, is heated: it will shrink when the activation energy for diffusion is available and entropic recoil occurs, even though it is not an elastomer.

•2.4 Affine deformation

In developing the ideas of elastic deformation (1§2), and their application to elastomers above, it is implicit that we are treating the bodies as being continua, that is, structureless and homogeneous: no atoms, molecules or other identifiable entities on any scale. Essentially, this is a macroscopic approximation, a purely geometrical approach to an idealized behaviour. The implication of this is that all points within the body must remain in the same spatial arrangement and relationship to one another, microscopically and reversibly, except for distances and angles. Literally, it is as if simple geometrical transformations were applied, scaling and shear, and all combinations, as mimics of the assumed behaviour under axial and shearing forces (Fig. 2.11). Such an exact process is called an affine deformation. (Translations and rotations are also affine, but trivial here.) An equivalent is the distortion of objects in a graphics program obtained by manipulating the ‘handles’, as indeed was used to create Fig. 2.11. Affine transformations preserve collinearity (i.e., all points lying on a line remain on a line) and ratios of distances (e.g., the midpoint of a line segment remains the midpoint).

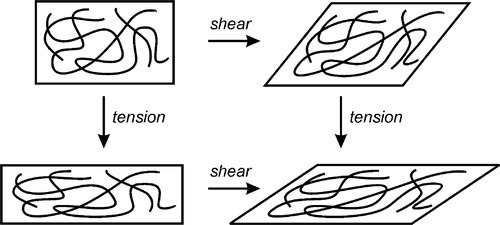
Unfortunately, in polymeric systems, and especially in elastomers, where the strains may be very large, the uncoiling of chains means that locally the spatial relationships between atoms on adjacent molecules or chain segments cannot be maintained. Such chains vary in length and orientation, and in pattern of folding, and so must unfold or draw in different ways. At this level, then, polymer deformation cannot be affine: the topology cannot be preserved. Accordingly, in cross-linked systems, for convenience, the deformation with respect to the nodes of the network (the cross-link or branch points) might be treated as affine. This means that the spatial relationships of those nodes are treated as if they alone were subject to the simple geometrical deformations, leaving the internode chains to find their own way, as it were, but still assuming that with respect to those nodes the system is microscopically and completely reversible. However, if the chains surrounding a node do not deform affinely, then the forces acting on the nodes, whether through bonds or molecular contacts, cannot be isotropic or even show a smooth consistent gradient over the whole piece: they must show relative movement beyond the affine prediction. In other words, in any such polymer there will be permanent deformation after any strain that causes chains or chain segments to slide past each other.

It is therefore the case that, for a simplistic approach, we may use the affine assumption as a useful approximation, but if we wish to consider local molecular effects it will break down. There are macroscopic phenomena due to the cumulative effects of the departure from an assumed ideal deformation, and there are consequences for dentistry arising from this. These issues will be further addressed in §11. It may also be noted that these considerations apply to any polymer system, not just elastomers, and to filled resins in particular (6§2.8). In both kinds of system, the filler particles may be taken as the reference points in the deformation, but there are further issues to consider when a filler is present. In fact, there are many other kinds of deformation, such as “keystone”, in which ratios of distances would not be preserved, for example, but where local relationships would still be, in the homogeneous model. This does not reduce the force of the argument above, but indeed strengthens it as making it more general.

§3 Effects of Fillers

As pointed out earlier (4§9), fillers are often used to modify the properties of a wide range of materials. They are useful in rubbers generally;^[2] for example, car tyres are heavily filled, and most dental impression materials contain fillers to a greater or lesser extent. Essentially, the problem is that while we require a low modulus in an impression material, that of pure elastomers is usually too low: an impression that distorted by sagging under its own weight would not be useful. We return to this point later (§12.9). Thus, we may view the design of an impression material in terms of the two factors: increasing the degree of cross-linking to attain good rubbery behaviour without the T_g being raised too high, and then adding in a filler to raise the value of the elastic modulus to suit the conditions of use.

To examine the mechanical effects of fillers in elastomers we can consider a small cylindrical element containing just one filler particle, and then apply an axial tensile stress (Fig. 3.1). The overall extension of that cylinder is defined by the positions of the end faces relative to the start, but if the filler particle has itself a higher modulus of elasticity than the surrounding rubber it will not have been extended to the same amount as the adjacent material. In fact, typical fillers are ceramic or similar very high elastic modulus materials, and their extension will be entirely negligible. Hence, in order that the end faces of the cylinder remain plane, the column of material above and below the filler particle must be extended by a proportionally greater amount than that of the surrounding cylinder (disregarding for the moment that the two sections of elastomer are connected and that the notional boundary between them is in shear).

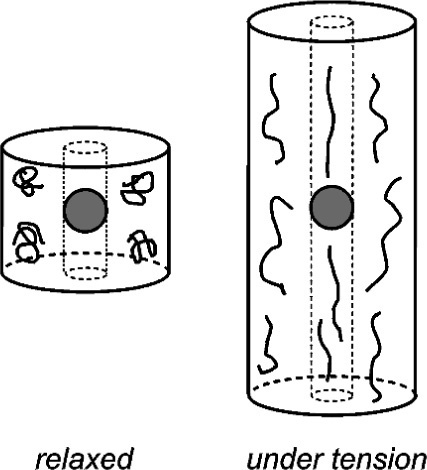
These extensions are easily calculated (Fig. 3.2). Taking the length between filler particle centres as the reference unit, the column with the filler particle is shorter by the filler particle diameter. The displacement, ∆L, is the same for both. It is then a matter of writing down the relative dimensional changes, i.e. the strains of the two sections. The strain in the filler column is expressed as a function of the cube root of the volume fraction of filler, ϕ_f, the value of which will be known from the formulation of the material. Thus,

ΔLL0<ΔLL0′=ΔLL0−ϕf1/3

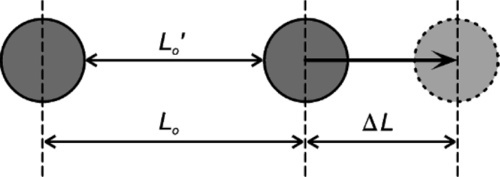
It is apparent that at high filler contents the strain locally may become quite large, i.e. when filler particles are very close together, even though the overall strain is small.

•3.1 Mullins effect

One of the conditions essential for the proper functioning of a filler in any system, and no less in impression materials, is that there is bonding between the matrix and the filler (6§2). If we take a close look at the possible arrangements of polymer chains between filler particles (Fig. 3.3), it becomes clear that the effects of overall deformation are not uniform for each one (cf. Fig. 2.6). Since the bonds will be made at random, the lengths of chain between such link points will also be random: a > b > c. Therefore, the amount of extension that each chain can withstand before being fully straightened (by bond rotation, 3§2) will vary, according to their lengths, entanglements (d) and cross-linking. Even at overall low strain some chain segments might be expected to break because the load that each now carries exceeds its strength, or, for some of the bonds to the filler to fail. Clearly then, these broken bonds or chains reduce the stiffness of the material at strains up to that which produced the breaks. By being converted to ‘free ends’, such sections of chain can contribute little or nothing to the resistance to deformation.

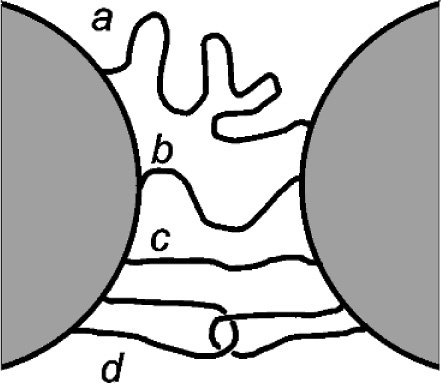
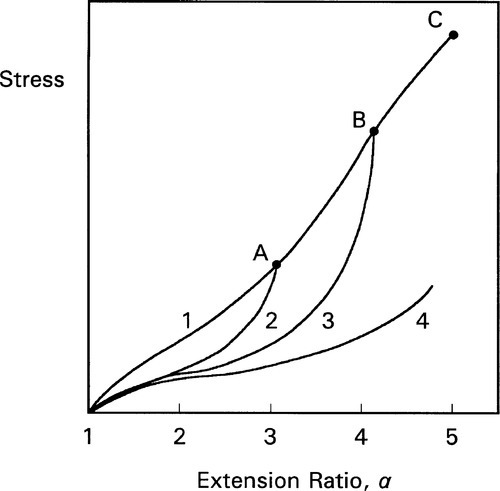
Thus, in the stress-extension curve 1 (Fig. 3.4), from the origin through ABC…, we observe unremarkable behaviour; superficially it is just as is shown in Fig. 2.5. But a number of chains or matrix-filler bonds must have been broken successively in the process of reaching point C. So, if the strain was taken only as far as A, and then returned to zero, the unloading stress vs. extension curve follows line 2 down to the origin. However, on reapplying the load, it is line 2 which is then followed, not line 1, back up to A. From then on the line ABC… would again be followed, smoothly continuous with line 1, as it would have done if the loading had not been interrupted. If, however, the extension were instead to be stopped at B, when the load relaxed to zero, line 3 would be followed back to the origin. Loading for the third time would follow line 3 from the origin, back up to B, and from there following BC…. The point is that straining beyond the previous maximum strain results in further bond breakages, whether they are within a chain segment or to a filler particle, making the material less and less rigid. Ultimately, a curve such as number 4 will be produced. It should be noted that it does not require every loading-unloading step of this example to be followed: if the interruption at point A were omitted, line 3 would still be the unloading curve from point B. This strain-dependent softening is called the Mullins effect. It can be seen to be similar to the strain-softening described in §2.2, but it is exaggerated by the presence of the filler.

It is now also apparent that similar effects will operate in filled-resin restorative materials, where bonded filler and a high degree of cross-linking is necessary (Chap. 6). Any stress which causes a polymer chain to break results in the material being less stiff afterwards below that stress. In other words, the effective number of cross-links has been reduced. Stress relaxation due to flow is thereby facilitated. This will be a contributing mechanism to long-term deterioration.

•3.2 Removing impressions

The Mullins effect is a second strong reason (see 4§6.1) for the removal of impressions in flexible materials from the mouth in one snap, and in the correct direction of least resistance. This is because each attempt involves some deformation, and each such attempt may result in some further softening of the structure in one region or another. This recommendation is not because the Mullins effect can be avoided, it cannot. However, in the course of several attempts, levering first one way then another, the total strain applied may easily exceed that which was strictly necessary. This makes the risk of distortion of critical parts of the mould under the forces of casting the model that much greater. Such parts are the margins of cavity preparations and the interproximal sections, which are very thin. This effect is in addition to the time-dependent viscous flow which will also be occurring during each of these extra periods of stress, the complications of the permanent deformations called ‘compression’, ‘tension’ and ‘shear set’ (4§8).

Strain softening has another more subtle effect. Ordinarily, one might measure a secant modulus (Fig. 1§13.1) for a filled rubber by noting the deformation of a specimen under a fixed load. It might be concluded from that result that the material was stiff enough to perform well in handling after taking the impression. However, those regions which have suffered large strains during removal, such as were in the interproximal spaces, will be significantly softer than such a simple measurement would imply, and especially at low loads, so that appreciable deformation in critical places may occur during the pouring of the model. Again, it is a matter of the design of the test reflecting the actual service conditions.

It can be seen that the ultimate tensile strength of a filled elastomer is not at all affected by the operation of the Mullins effect: all the bonds that are broken in succession would be broken in the same sequence anyway (if we assume that the direction of loading is constant). However, after stress cycling to any level below failure, the area beneath the curve for a subsequent cycle is reduced. Hence, the energy required for failure decreases according to the extent of prior loading; this is equivalent to a reduction in the tear strength of the material. In other words, the work of fracture has already been partially supplied in the earlier stress cycles; there is no violation of physical law.

•3.3 Importance of shear

The rheological properties of impression materials are important to their dental use – even when they are set and supposedly not capable of flowing. This arises from, on the one hand, the deficiencies of the structure (in the chemical sense) permitting flow, and on the other hand the internal stress conditions which are generated during any kind of loading except pure hydrostatic. It is shear that causes flow (4§3), and where there is both tension and compression acting at a point (even if it is only the one arising from the other as an ‘effective’ stress due to Poisson strain; 1§2.2, 6§2.7), there is a resultant shear stress. To this is added the local shear due to the mismatch of strain in adjacent columns of material (Fig. 3.1). This shear then causes deformation of the shape of a polymer chain (Fig. 3.5).

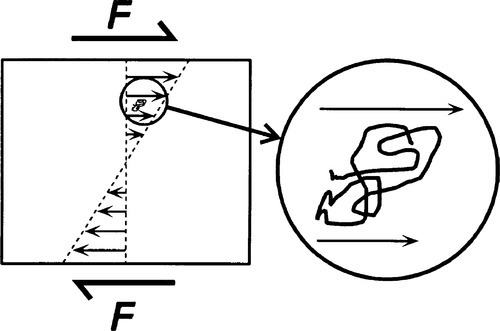
It then follows that since the polymer chains in their sheared condition must relax, and because this depends on chain-segment diffusion, the process takes time. Thus the Kelvin-Voigt or retarded component of elastomer rheological behaviour arises naturally from the structure. If any portion of the system is not constrained by cross-links, entanglements or bonding to filler, true flow must occur to give permanent deformation as well (§2.4). This points out the underlying necessity of viewing these processes at the molecular level if the clinical behaviour and handling requirements are to be understood.

•3.4 Filler factors

The amount of filler has, as might be expected, a direct effect on the modulus of elasticity of the composite structure that is the filled impression material (6§2). In this respect the properties are directly controllable to give the desired values (bearing in mind the compromises which may be required due to viscosity effects; 4§9, 6§3). There are, however, additional effects operating which have to be taken into account: particle shape, surface activity, and specific surface area. Fig. 3.6 shows the effect of increasing the volume fraction of two different fillers on the modulus of a rubber. It is too simplistic just to require ‘bonding’ between matrix and filler, the strength of that bonding (which need not be restricted to covalent bonds) and the areal density of the bonds, determine how much the matrix is constrained. In fact, for the very large quantities of filler involved for impression materials, it is probably not economic to treat them with special coupling agents. Instead, reliance may be placed on mechanical key or natural reactivity.

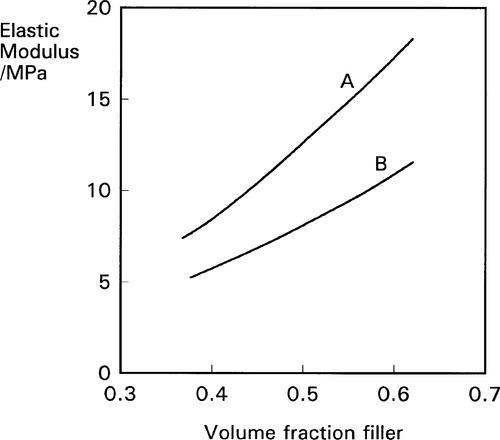
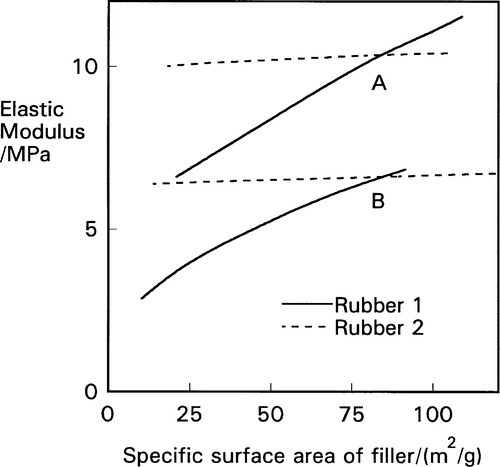
In addition, the specific surface area of the filler, or the particle size, is also a means of control effective with some materials. As with the effects on viscosity, mediated through a stationary boundary layer (Fig. 4§9.3), the more material is held in this layer the less is ‘available’, as it were, to deform. The nature of the filler-matrix interaction is also dependent on the detailed nature of the polymer, as indicated by the differences between two types of rubber for the same fillers (Fig. 3.7); the one material is practically unaffected. It should be apparent from Fig. 3.4 that if a filler is to be effective in increasing the modulus of an elastomer, and therefore any matrix material, it must be bonded to that matrix. Were it not, the Mullins effect would not be observable to such a large extent, although chain entanglement and cross-linking effects would remain.

The so-called elastic impression materials are based on polymers which in principle are capable of very large extensions with near perfect elasticity. In practice, this is rarely achieved because of the need to realize curing at low temperatures and in relatively viscous materials (which inhibit reactant diffusion), when the completeness of the reaction must therefore be relatively low. The demands of the clinical context require that any chemical reaction for cross-linking be very rapid, that is, using highly-reactive substances. But reaction can only occur after diffusion has brought the reactants together, and this becomes more difficult as cross-linking proceeds. In addition, high filler contents are often necessary to obtain sufficiently stiff materials as end-products. The principal types currently available are based on polysulphide, polyether and silicone rubbers.

§4 Polysulphide

The polysulphide rubber impression materials, sometimes very loosely called ‘rubber base’ or ‘thiokol’, are based on a single bulk commercial liquid polymer product labelled “Thiokol LP-2”. In order to understand some aspects of the structure and behaviour of the dental product, it is necessary to review the manufacture of the main ingredient.

•4.1 Manufacture

The industrial manufacture of LP-2 involves first reacting bis(2-chloroethyl)formal:

Cl−C2H4−O−CH2−O−C2H4−Cl

which has reactive chlorine end-groups, with sodium polysulphide. This reaction eliminates NaCl, replacing pairs of chlorine atoms with an -SS- group, creating a high polymer. This on its own would necessarily be composed of all straight chain molecules, and so would be quite useless for making a rubber because it could not form a network structure. Branch-points are therefore introduced by including in the reaction mixture 2 mole percent of 1,2,3-trichloropropane, a cheap and readily available trifunctional reactant, the chlorine reacting in the same way as for compound 4.1. The result of this first reaction is therefore a polysulphide rubber, but since it is now already nearly completely polymerized it is unusable at this stage. Hydrolysis with a strong base breaks this structure down again, cleaving the polymer at the disulphide linkages, and leaving the new terminal sulphhydryl groups, -SH. This may seem a strangely roundabout means of obtaining the material, but it can be relied upon as being an economically valuable route.

The golden yellow, somewhat viscous liquid thus obtained is the polymerizable product which, with its moderately high number average molecular weight of about 4000, is best described as prepolymer. It is this material that forms the basis of the product supplied to dentistry. Contrary to many descriptions, the most common type of molecule in this liquid is the monomeric dithiol version of the dichloride precursor above:

HS−C2H4−O−CH2−O−C2H4−SH

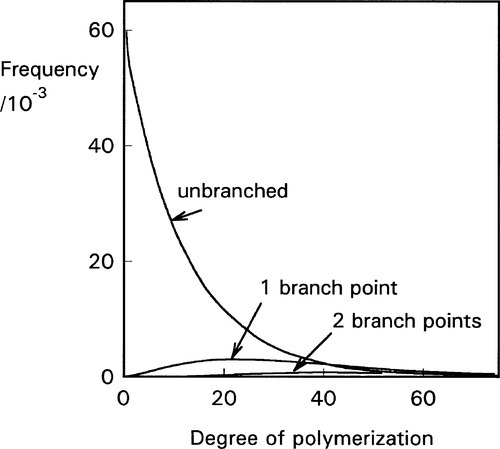
with dimers, trimers and so on in diminishing proportion (Fig. 4.1).^[3] However, the average degree of polymerization is about 24. There are, of course, a variety of other kinds of molecule which have incorporated the trichloropropane moiety and which are therefore branched, to give a variety of Y-, H- and more complicated shapes which by being polyfunctional maintain the ability to create a network when the polymer is (re)formed. The viscosity and the average molecular weight arise from the presence of the relatively smaller numbers of very large molecules (Fig. 4.1). The presence of low molecular weight (and therefore volatile) thiol impurities give this class of material their characteristic and unpleasant smell.

•4.2 Setting reaction

Now, to convert the prepolymer into a rubber, by reaction between the thiol groups (the ‘setting’ that occurs when taking an impression), an oxidizing agent is required to remove the hydrogen. The most commonly used is lead dioxide (N.B. not peroxide), the very dark brown substance which gives some polysulphide impression material products their characteristic colour.

The initial step is the oxidation of two thiol groups to form a disulphide bridge (Fig. 4.2), with the elimination of water: this is therefore a condensation reaction. Notice that the reaction

PbIV+2e−⇒Pb++

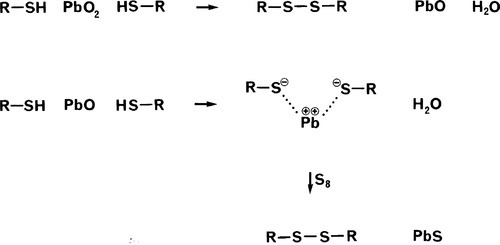
is a reduction of the lead, corresponding to the oxidation of the thiol groups.

However, there is a tendency for the lead monoxide by-product formed here to react with further thiol groups itself, because it is still sufficiently reactive as a base with respect to the acidity of the thiol hydrogen. However, since this is only a salt-forming reaction, again eliminating water, it forms an ionic bridging complex instead of a covalent bond. (Essentially, Pb⁺⁺ is not a strong enough oxidizing agent to abstract the electrons from the sulphide />