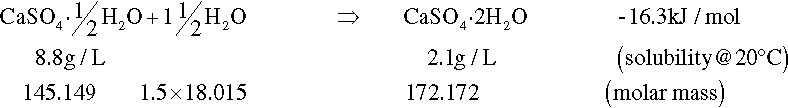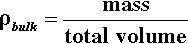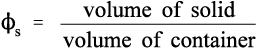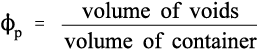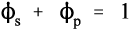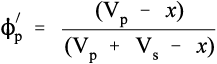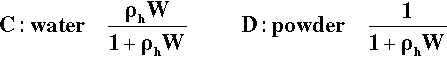Gypsum products are probably the single most used class of material in the whole of dentistry, at least in terms of mass. This arises from the fact that models of the dentition provide the basis of the majority of restorative treatments: full and partial dentures, bridges, crowns, and inlays, as well as for orthodontic work and reconstructive surgery, both for study of the case and as a template on which to work for many laboratory procedures. Then there are impression materials and casting investments relying on the same chemistry. These materials provide important links in a chain of processes leading to the final treatment outcome. In view of this central position, gypsum products must be understood thoroughly if both their own use as well as the processes going on around them are to be effective. In fact, the design of some materials and procedures is based on the inadequacy of gypsum products in one respect or another. It is the low cost of the raw material that primarily contributes to its dominance, but this should not be considered as diminishing the value or importance of the resulting dental products.

§1 Basic Reactions

Gypsum is the common name of the mineral calcium sulphate dihydrate, which is mined in various places around the world and now is also being produced in a relatively pure form as a by-product of sulphur dioxide removal processes for power station exhaust gases. It has wide application, particularly in the building industry as plaster for finishing internal surfaces, but ‘plaster casts’ on broken limbs are possibly the most familiar use. Plaster of Paris, dental plasters and dental “artificial stones” are all manufactured by the dehydration of the dihydrate, using various processes, but they all have a common underlying chemistry.

•1.1 Dehydration

On heating, dehydration of the dihydrate occurs in two distinct stages. The fairly rapid loss of three quarters of the water of crystallization at about 130 °C gives the hemihydrate (Fig. 1.1). Further and now complete dehydration occurs at higher temperatures to give anhydrite. This has two crystal forms with differing reactivities with respect to water. The orthorhombic form, obtained by heating above 200 °C, is so slow in reacting with water that it is known as dead-burnt plaster; it does not form a usefully setting mixture with water. The crystal structures of the different forms are quite distinct from each other. The water molecules in the dihydrate are found in alternate double layers with the calcium ions and sulphate groups (Fig. 1.2),^[1] and so its removal results in the destruction of that crystal. It may be deduced from the temperature required for dehydration that the process requires much energy, implying that at room temperature the dihydrate is a relatively stable form compared with the hemihydrate. It is this difference which provides the driving force for the setting reaction.

•1.2 Rehydration

Although all of the dehydration products will react with water to give the same reaction product (the dihydrate), the rates are considerably different. Dental gypsum-based materials all rely on the fairly prompt reaction of the hemihydrate with water to produce the less-soluble dihydrate:

< ?xml:namespace prefix = "mml" ns = "http://www.w3.org/1998/Math/MathML" />CaSO4·12H2O+112H2O⇒CaSO4·2H2O‐16.3kJ/mol8.8g/L2.1g/Lsolubility@20°C145.1491.5×18.015172.172molar mass

The mechanism is straightforward: hemihydrate readily dissolves in water at low temperature, but the solution becomes supersaturated with respect to dihydrate before it is saturated with respect to hemihydrate. As a result, dihydrate may commence to precipitate from the solution if it is appropriately nucleated, and it does so by the formation of needle-like crystals. This continuous precipitation then prevents the solution from becoming saturated with the hemihydrate, which therefore continues to dissolve. The process can continue until all hemihydrate is consumed, or other factors interfere, such as precipitated material completely occluding remaining hemihydrate, or insufficient water being present.

It can be deduced from this that there are a number of possibilities for intervening in the process and controlling the reaction, and so of modifying the setting rate of gypsum-based materials. These include control of the solubility of the reactant and product; the rate of solution of hemihydrate; the rate of nucleation of new product crystals; the crystal habit or morphology, and hence the rate of crystal growth; as well as modifying the amounts of reactants. To start, let us consider the unmodified reaction and its consequences. First of all, it is found that the amount of water required to mix a usably fluid slurry is rather greater than that calculated to be required for the complete stoichiometric reaction of the hemihydrate – the set material is still wet. It is necessary to recognize that this apparent contradiction arises from two quite separate considerations.

§2 Mixing Liquid

Where a liquid is to be mixed with a powder or other granular material, the question arises of the amount of liquid needed for proper mixing. Although perhaps most obvious in the context of gypsum products, it is of direct relevance to many dental materials: acrylic, amalgam, cements, investments, filled resins, and so on. Exactly the same factors and compromises apply in all of these cases, and their handling should also be considered in the same way. The first issue is centred on the concept of gauging liquid.

•2.1 Volume fractions

For any particulate, non-fluid material (“powder”) the amount that can occupy a given volume when it has been allowed to settle depends on the particle shapes and their relative size distributions. It does not depend on the overall or mean size of the powder particles. We are, of course, assuming that the container into which the powder is imagined to be put is very much larger than the particles, so that packing at the walls is not a consideration. Finer particles with the same shape and relative size distribution do not pack any better. Such packing is said to be scale invariant. This can be understood by considering a photograph of a cross-section of such a packed powder: the magnification does not affect the proportions of solid and pores.

The amount of powder in a given volume can be expressed by the bulk density:

ρbulk=masstotal volume

However, a more useful measure is the volume fraction of solid, to which we may give of solid, to which we may give the symbol ϕ_s:

ϕs=volume of solidvolume of container

Similarly, the volume fraction of pores in that bulk powder, ϕ_p, is given by:

ϕp=volume of voidsvolume of container

This latter quantity properly must also include any porosity within the powder particles (as is the case with dental plaster, for example) as well as the interstices between particles. Hence, by definition,

ϕs+ϕp=1

•2.2 Gauging volume

In order that a fluid slurry be made from such a powder, a volume of liquid at least equivalent to ϕ_p must be added first. If this were not so, of course, the particles of solid would remain in contact with each other and thus inhibit flow markedly by frictional effects. Certainly, there would be that much porosity left in the final material if less liquid than the equivalent of ϕ_p were added; this porosity is, in general, undesirable because it reduces strength (§8). The volume fraction of pores in the bulk powder, ϕ_p, is commonly identified as the gauging volume of liquid for that powder. It is not necessarily (or even likely to be) the same as the volume of liquid required for the successful execution of the technique and due attention must be paid to the needs of the application. There are three principal reasons for this.

The gauging volume is only a measure of the free space in the packed powder, nothing else. Thus, and firstly, in defining gauging volume no account is, or should be, taken of the amount of liquid required for reaction: sand from the beach has an associated gauging volume, as does dental porcelain powder – and there are no setting reactions there. If it is a reacting system, we can determine only whether the gauging volume is greater or less than is required for complete reaction. Sometimes there will be excess liquid at the end of the reaction (as is usually the case with plaster and stone) and this remains detectable as liquid; sometimes there is none, when there is deliberately excess, unreacted, powder (as in amalgam and dental cements). Denture base acrylic requires at least sufficient monomer added to the powder to fill the spaces and avoid air porosity, but of course this monomer should all be converted to polymer ultimately.

Some care is required in considering gauging volume as it is not a fixed quantity: it depends on the state of consolidation or settling of the powder. That is, when a powder is poured into a container, the particles will settle in a random manner but limited by inter-particle friction. The rougher the particle, the worse the effect of this will be, leading to low density packing. Vibration, however, can overcome that friction and allow better settling, and greater density, with (of course) lower gauging volume. Depending on the nature of the powder, differences of 10 – 20% may be observed between the density in the freshly-poured state and the greatest attainable value (without crushing), the tap density, although this is hard to approach without a lot of effort. There are implications for this variation of density in several areas (4§7.9, 15§4.1, 15§6.1, 25§1.2). The problem is one of reproducibility. In general, the as-poured condition is a better reference state.

•2.3 Dilatancy

Secondly, there is the phenomenon of dilatancy. When a powder is allowed to settle under gravity, each particle tends to fit as closely as possible into the available space, particularly if vibrated (this is commonly experienced with alginate impression material powders which are usually measured out by volume, 15§4). Most powders are irregular in shape, not spherical, so that if any particle were to be rotated the distance between its centre and that of an adjacent, contacting, particle must increase to allow that rotation to continue. Thus, when a powder is stirred, all particles will tend to rotate to some extent from their preferred (well-packed) positions (Fig. 2.1). If they move away from each other the bulk volume of the powder must increase, and therefore so must the gauging volume. This is dilatancy.

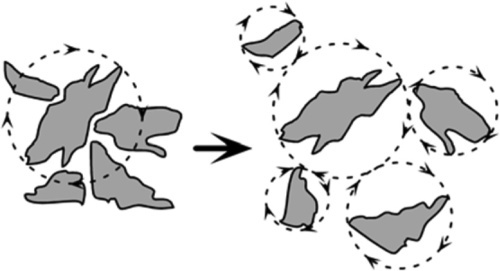
Beach sand shows the effect very well: if one walks across sand wet enough to have a smooth, glossy film of water at the surface, around one’s foot when pressure is applied and while the sand is moving, a region appears to go dry or, at least, matte; it shows loss of gloss. This is because the locally-increased pore volume allows the surface water to drain away, due to the small disturbance to each individual sand grain’s position. So, to allow a slurry to be easily stirrable, somewhat more liquid must be added than the static gauging volume would suggest. This extra liquid is to allow for the dilatancy. Stirring with anything less would tend to introduce air bubbles into the mixture, again an unacceptable occurrence, at the very least because of the reduction in strength and stiffness that this causes.

Dilatant mixtures are easily recognized because they become harder to stir the faster one tries to stir them. It follows then that the liquid to be added to allow for the dilatancy of a given powder is a function of the stirring rate, at least up to the point where the powder particles are suspended in the liquid medium and capable of freely rotating without interfering with their neighbours. This limited amount of added liquid may be termed the dilatancy allowance. It may be viewed as the difference between the gauging volumes of the static, settled powder and that same powder when agitated – the extra gauging volume required by dilatancy.

•2.4 Minimum mixing volume

Beyond that point the fluidity of the mixture depends on the dilution of the slurry: the more liquid, the easier it will flow. It follows then that for a conveniently fluid mixture, for stirring, moulding and pouring, the actual liquid volume used must include an allowance, the dilution volume, along with those for gauging and dilatancy. However, the actual allowances made for dilution may vary somewhat with the application, even within one kind of product as, for example, when ‘restoration’ and ‘luting’ mixes of certain cements are defined with different powder-liquid ratios. We can therefore define the minimum mixing volume as the sum of the gauging volume and the dilatancy allowance, although recognizing that this might not (indeed, probably not) be usable in practice.

Where appreciable reaction occurs between the time of contact of liquid and powder in any such system (cements, amalgam and the like), the proportion of liquid actually present at the point of use will be different from that at the start, and other structures may be forming: the viscosity will rise and could make the material unworkable, damaging the structure that is forming by further manipulation. Thus, the liquid volume to be used for mixing must allow for that change. The actual working mixing volume therefore allows for this effect as well as the technique-dependent dilution volume, extra liquid is included to allow for loss by reaction – the reaction allowance. It is stressed that this is a purely physical concept because it relates to the physical (rheological) properties of the mixture in relation to its handling. The amount of liquid required for reaction, the chemical process, is an entirely separate consideration. The two should not be confused. However, it should be recognized that because of this allowance the initial viscosity when freshly-mixed according to instructions may appear to be too low: the temptation to thicken it up by adding more powder must be resisted.

Thus, the recommended working mixing volume can therefore be defined as involving allowances for

• gauging: filling the spaces in the settled powder

• dilatancy: allowing for particle tumbling on stirring

• dilution: to attain the appropriate fluidity for the application

• reaction: to compensate for liquid volume fraction reduction as the material sets.

•2.5 Wetting

The gauging volume should not be described as the minimum liquid required to ‘wet’ the powder. In the limit one may say that the minimum in that sense is just a monolayer of the liquid over the entire surface of the powder. The size of the water molecule is such that about 0.5 mg or 30 μmol, just 1/400th of a drop, is required to cover 1 m², so that for a powder such as a dental stone, which may have a total surface area of greater than about 1 m²/g, only about 30 mg of water are required to ‘wet’ a 60 g portion of powder, substantially less than the 15 mL or so gauging volume. The fact is, this amount of water is probably present already, adsorbed from the atmosphere almost immediately upon exposure. Such a layer of adsorbed water is indeed likely to be present on almost every material’s surface anyway.

However, when mixing powder and liquid it is easy to trap air bubbles which contain dry powder, whether it is a gypsum product, alginate, investment, or cement, even though there may be well in excess of the gauging volume present. The mixing technique used, which always has some ‘wiping’ motion, is intended to break up and disperse such islands of dry powder and ensure that it all gets wetted. Certainly, with gypsum products and alginate, the method of adding powder to liquid (rather than the other way around) is intended to reduce the risk of that problem occurring and make correct mixing easier.

One therefore has to distinguish carefully between the sufficiency of the liquid present to achieve wetting – a purely surface effect, and the adequacy of the mixing process, which refers to meeting the conditions for the entire bulk of material. We may therefore more usefully refer to the condition of the gauging requirement being met by saying that the bulk, undisturbed powder is saturated, that is, it cannot hold any more liquid in its porosity. A parallel common usage may be found when we speak of a sponge or a cloth being ‘saturated’ with water – it can hold no more. Sometimes the term wetting out is used in dentistry in the same sense of saturating a powder, but it is not as clear and distinct as a condition concept, although the process is clear enough.

§3 Dental Products

The amount of mixing water required for a given fluidity varies with the nature of the hemihydrates powder. The particles of plaster are very porous and often relatively large (because this depends on the grinding it is given by the manufacturer). In addition, being irregular the particles do not pack together very well, and being rough causes the friction between them to prevent settling. This material therefore requires a larger amount of gauging water than does dental stone, which is composed of regular, smooth and non-porous crystals that pack and settle well. These crystals also tend to be quite small. These variations are due to the different methods of commercial preparation.

•3.1 Manufacture

If dihydrate is heated in air to about 130 °C, that is, calcined, at atmospheric pressure (Fig. 3.1), the crystal structure is rapidly disrupted as part of the water boils away, leaving a material with the composition of hemihydrate. This is plaster, and it has very poor crystallinity because of the lack of a medium through which the ions could diffuse to form good crystals. The calcined mass of plaster must be mechanically broken up and ground to a usable powder, but the particles remain irregular and porous.

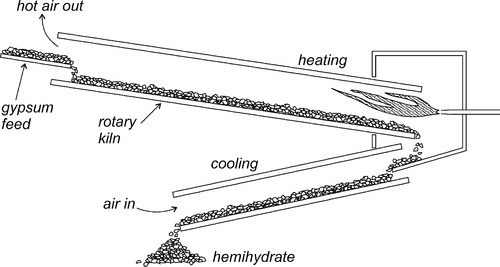
Artificial stones, on the other hand, may be produced by autoclaving at high pressure, or by boiling dihydrate in a solution of calcium chloride (or other salt); both procedures raise the boiling point of the liquid present considerably. These conditions cause the decomposition of the dihydrate, because the temperature is high enough, but more importantly the presence of the liquid water permits the recrystallization of the hemihydrate. Such crystals are then well-formed, regular, and necessarily non-porous. Consequently, they pack rather better than plaster particles, hence the lower gauging water requirement. The distinction between the various grades of artificial stone depends essentially on the variation of the crystal habit of the hemihydrate powders, as controlled by the solution environment in which they are growing (i.e. the types and concentrations of other ions). The more equiaxed these crystals, the better they are able to pack in the bulk powder, the lower the mixing water requirement, the denser and harder the set material. The manufacturers’ goals include finding the processing conditions that produce the highest packing density hemihydrate powder possible if a high strength, high hardness material is desired.

These particle properties are responsible in part for the choices made in the principal dental applications. Thus, dental plaster is used for the bases of models because it is cheap and easily shaped (i.e. weak), as well as because the setting expansion (§5) is not very important. The same kind of material is also used in impression plaster (see 27§2.4), but here primarily because it is weak enough not to run the risk of splinting the patient should there be an undercut and also to facilitate its removal from the model prepared in that impression (from artificial stone); however, anti-expansion solution is necessary here (§7.5). Should a plaster impression be broken, as is commonly the case, the fact that it is a rigid and brittle material means that it can be reassembled using sticky wax without appreciable loss of accuracy. Plaster powder is the reactive setting ingredient of gypsum-bonded casting investments (17§3.1), while powdered dihydrate – gypsum itself – is commonly used in alginate impression materials (7§9) as a source of cross-linking calcium ions because of its low but slow solubility (some alginate products may also use hemihydrate for this purpose). Autoclaved hemihydrate powders are used in model stones, as used for mouth models, and the harder die stones, which are used for the dies on which wax patterns for castings may be fabricated. The choice here is because their strength and hardness resist damage during handling, damage which would be detrimental to the accuracy and success of the final device. These different gypsum products may be variously coloured according to manufacturer and intended use, but this has no importance except for product identification and contrast with other materials.

•3.2 Minimum mixing volume

As described in §3.1, the packing of the bulk powders is better when the particles are more regular, equiaxed and solid (i.e. non-porous). That is, the bulk density (§2.1) is higher. In other words, a given mass of artificial stone powder occupies a smaller volume overall than does the same mass of plaster powder (Fig. 3.2). Thus the gauging volume per unit mass of powder will automatically be much lower for the stone. Note that the volume fraction of pores does not change as rapidly as the bulk volume when the packing is better:

ϕp′=Vp‐xVp+Vs‐x

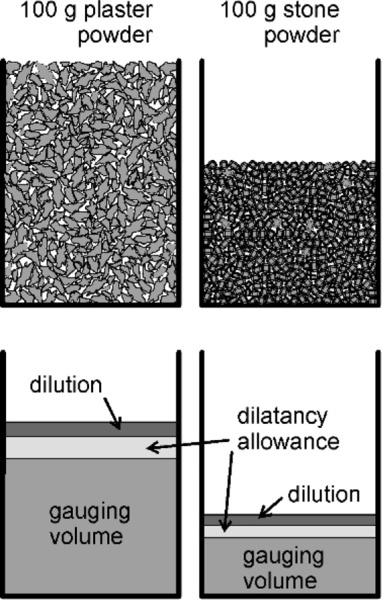
If the bulk volume (V_p + V_s) is reduced by some amount x, this is also the reduction in the actual volume of pores (compressing the powder cannot change the actual volume of solid). In effect the reduction in the numerator of the right-hand side is diluted because the denominator is reduced as well.

The more equiaxed particles also give rise to less dilatancy, so less water needs to be allowed for that. This also has an effect on the dilution allowance required for a sufficiently fluid to be easily workable. Thus the working liquid volumes can differ greatly. Typical values are around 60 mL water to 100 g plaster and 30 mL to 100 g for artificial stone. The ‘improved’ stones (which have even better crystal shapes) may require as little as 23 mL / 100 g.

Note that there would be no benefit whatsoever obtained from helping the powders pack better by vibration or compression (§2.2). Dilatancy ensures that the actual bulk volume when stirred depends on the particle shape, not on the original packing, even if proportionally the dilatancy allowance would seem to be greater. Any consolidation is undone on stirring. Again, note the difference between minimum mixing volume and working mixing volume.

§4 Mixing Proportions

The hemihydrate mixtures used in dentistry are usually characterized by stating the water: powder ratio, expressed in units of mL/g.¹ This measure, however, whilst in general use for the practical handling of the material and entirely sensible in that context, is not very informative about the chemistry of the system, or very helpful in trying to understand mechanical properties. In particular, the scale is open-ended, there being no limit to the amount of water that can be taken. We shall therefore follow the lead given in §2, and convert to fractional forms. These have natural limits.

•4.1 Mass fractions

The water: powder ratio is numerically the same as the mass of water (W) added to unit mass of powder. Then, because the density of liquid water is very close to 1 g/mL at ordinary temperatures, the relative total mass of a mixture may be written as 1 + W, i.e. for each gram of powder there are W grams of water. The mass fractions of the two components are then simply given by the following:

A:waterW1+W

B:powder11+W

•4.2 Volume fractions

But, as remarked above (§2), volume fraction is a more informative measure. The definition of density is mass per unit volume, so the volume of a given mass of substance is obtained by dividing by its density. The individual volumes of the components are therefore 1/ρ_h and W/ρ_w for hemihydrate and water respectively. Expressions A and B can be converted to give the volume fractions of the components by first replacing each term by the corresponding volume, then multiplying each term by ρ_h to avoid the presence of reciprocals, noting that ρ_w = 1:

C:waterρhW1+ρhWD:powder11+ρhW

•4.3 Excess water

Knowing the stoichiometry of the reaction, the relative amount of water required for reaction is determined by the ratio of the molar mass of the extra water (1·5 × 18·02) to the molar mass of the hemihydrates with which it will react, i.e. 27·03/145·15 = 0·186. By subtracting this quantity from the actual water added, the excess water is found from A and C respectively:

E:bymassW−0.1861+WF:byvolumeρhW−0.1861+ρ