Orthognathic Surgery Treatment Planning
Part I: The Importance of Proportions and Symmetry to Establish Ideal Facial Aesthetics
Fundamental Concepts
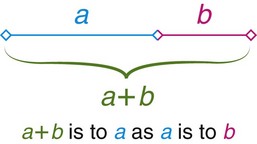
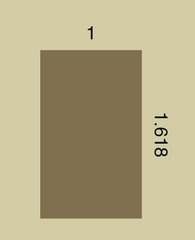
We use the word proportion to describe the comparative relationship between parts of things in an attempt to describe harmonious and disharmonious relationships between different parts of a whole.13,14,49,92 The first clear and still unsurpassed definition of what has become known as the “golden ratio” was put into words by Euclid of Alexandria around 300 B.C.5,29,42–44,61 Euclid is best known as the founder of geometry, which is a branch of mathematics that involves the use of deductive reasoning.68 In the most pure way, Euclid defined a harmonious proportion derived from the simple division (sectioning) of a line into what he called its “extreme and mean ratio.”61 In Euclid’s own words, “[a] straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.”98,99 (Fig 12-1) This ratio was defined by Euclid as the “golden ratio.” Interestingly, this ratio represents a never-ending (irrational) number 1.6180339887…. The common symbol for the golden ratio is the Greek letter tau (τ), the meaning of which is “the cut” or “the section.” It was later renamed phi (Ψ) after the Greek sculptor Phidias, who was said to have employed it61; this is described in more detail later in this chapter.
A definition of the word beauty can be found in Webster’s unabridged dictionary as “the quality which makes an object seem pleasing or satisfying in a certain way.”63 The golden ratio is said to be an important feature that is found in many classically beautiful works of art, architectural structures, objects designed for human use, the music of the great composers, and most of what is found in nature.17,18,20,45,49,57,58,67,68 “Perfect” proportions are found throughout the art world and throughout the centuries. Objects of “classic” beauty and “attractive” forms found in nature consistently reveal the golden ratio.40 However, an important question remains: “Does form really follow function?” Richard Buckminster Fuller (1895-1983), a great American architect and writer, once stated, “When I am working on a problem, I never think about beauty. I think only of how to solve the problem. But when I finish, if the solution is not beautiful, I know it is wrong.”61
In their simplest form, attractive facial images—whether in drawings, in photographs, or in reality—seem to incorporate a consistent symmetry of proportion. It has been stated that most people have a common appreciation of what is attractive when they visualize it even if they cannot quite explain why. This has been demonstrated across cultures and throughout the ages, and it has been relatively consistent in art and photography.6,19,27,32,48,53,54,63,77,81,80 A strict mathematical formula may not be required to define classic attractiveness, but the question remains: “Can the golden ratio (a mathematical formula) be found in these commonly agreed upon beautiful images?”
Evolution in Thinking
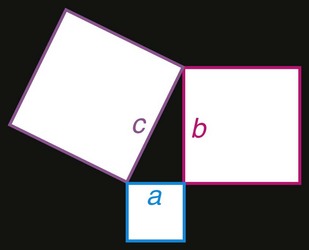
Pythagoras (570 B.C.-522 B.C.) coined the terms philosophy, defined as “a love of wisdom,” and mathematics, defined as “that which is learned.”47 He described a philosopher as someone who “gives himself up to discovering the meaning and purpose of life itself—to uncover the secrets of nature.”100,42,61 Pythagoras and his followers (i.e., Pythagoreans) are best known for their role in the development of mathematics and the application of mathematic principles to the concept of order in the world. The Pythagorean theorem states that, in a right-angle triangle, the square of the hypotenuse (i.e., the side opposite the right angle) is equal to the sum of the squares of the other two sides; in other words, a2 + b2 = c2 (Fig. 12-2).9
According to legend, Pythagoras discovered that musical notes could be translated into an orderly mathematical equation by observing a blacksmith at work. He thought that the sounds emanating from the blacksmith’s anvils, when they were struck, were both beautiful and harmonious. By studying the blacksmith’s tools, Pythagoras discovered that the emanating sounds were “simple ratios of each other and that one was half the size of the first and so on.”61,100 He then constructed metal bells with each sized in equal ratio to the next. When he struck the proportionately sized bells, harmonious tunes resulted in the same way that he had observed with the anvils. The harmony that resulted when striking the proportionately sized bells or anvils, according to Pythagoras, was beautiful.
Pythagoreans also believed that “harmony existed with the spheres of the planets and stars according to a similar strict mathematical equation and thus produced a similar “planetary symphony.”61,100 Pythagoras later discovered flaws in the purity of mathematics. He was the first to write of having knowledge of a number that is “neither a whole—nor a ratio of two whole numbers.”61,100 This discovery was said to have overwhelmed his perspective of a world based on the intrinsic properties of whole numbers and their ratios. He could not find a role for irrational numbers in this world.44 Pythagoreans believed that the existence of such irrational numbers was so horrific that such numbers represented some sort of cosmic mistake and thus should be suppressed and kept secret.
Pythagoras and the Pythagorean school made a great impact in various fields, from sculpture to philosophy.55 Polykleitos (450 B.C.) is a vivid example of the positive influence of Pythagoras’ ideas. Polykleitos consciously created a new approach to sculpture that is immortalized in his treatise Kanon and visually depicted in his design of the male nude (also known as Kanon), which exemplified his aesthetic theories regarding the mathematical basis of artistic perfection.69 His general artistic aims were clarity, balance, and completeness. The Kanon‘s basic principles are represented in Polykleitos’ best-known bronze sculptures, including Doryphoros (Fig 12-3); Diadumenos (Fig 12-4); and Astragalizontes. These sculptures are said to have a precise commensurability (i.e., “symmetria”) of all of the parts with one another. The idea of “symmetria” comes from the Hippocratic principles of “equilibrium” and “rhythmos.”100 Polykleitos also said that “perfection comes about little by little through many numbers.”61,100 This meant that a statue should be composed of clearly definable parts, all of which are related to one another through a system of ideal mathematical proportions and balance. This was expressed in terms of the ratios established by Pythagoras, including in the perfect intervals of the musical scale: 1 : 2 (octave), 2 : 3 (harmonic fifth), and 3 : 4 (harmonic fourth).

Figure 12-3 Doryphoros by Polykleitos. From http://en.wikipedia.org/wiki/File:Doryphoros_MAN_Napoli_Inv6011-2.jpg Photograph by Marie-Lan Nguyen. Creative Commons License: Attribution.

Figure 12-4 Diadumenos by Polykleitos. Image Copyright © The Metropolitan Museum of Art, Image source: Art Resource, NY.
The Polykleitos school continued after Polykleitos’ death and included at least 20 sculptors and artisans through early 200 B.C. They were defined by their adherence to the Kanon and its principles of balance and definition (i.e., clarity in the separation and relationship of the parts to the whole). Polykleitos’ students would think beyond sculpture in bronze; this included the work of Polykleitos’ son, Polykleitos the Younger, whose architectural design of the great theater of Epidaurus was remarkable for its harmony and balance (Fig. 12-5).100 Within the theater, the place for spectators was divided into two tiers: the first one had 34 rows of places, and the second one had 21 rows (i.e., 34/21 = 1.61…). The angle between the theatron and the scene divides the circumference of the basis of the amphitheater in a ratio of 1.618…. Interestingly, both of these meet the standards of the golden section, which was soon to be precisely and clearly defined by Euclid, as described later in this chapter.

Figure 12-5 Theater of Epidaurus in Epidaurus, Greece. Copyright 2013 BootsnAll Travel Network, LLC. All Rights Reserved. http://www.greecelogue.com/the-ancient-theater-of-epidaurus.html.
Polykleitos’ greatest work is said to be the sculpture Doryphoros (i.e., “spear-bearer”), which is considered one of the best-known sculptures of the classic era.100 During the second century A.D., Galen would write about Doryphoros as the perfect visual expression of Greece’s search for harmony and beauty, which is rendered in the perfectly proportioned sculpted male nude. Galen stated the following:
Chrysippos [or Doryphoros, the spear-bearer] holds beauty to consist not in the commensurability or “symmetria” [i.e., proportions] of the constituent elements [of the body], but in the commensurability of the parts, such as that of finger to finger, and of all the fingers to the palm and wrist, and of those of the forearm, and of the forearm to the upper arm, and in fact, of everything to everything else, just as it is written in the Canon of Polyclitus [Polykleitos]. For having taught us in that work all the proportions of the body, Polyclitus supported his treatise with a work: he made a statue according to the tenets of his treatise and called the statue, like the work, the “Canon” [i.e., Kanon].61,100
A contemporary of Polykleitos was Phidias (480 B.C.),100 who is regarded as one of the greatest sculptors of bronze, gold, and ivory from Greek antiquity. Phidias’ statue of Zeus at Olympia was considered one of the seven manmade wonders of the Ancient World (Fig. 12-6). He also created the statue of the Goddess Athena on the Athenian Acropolis (Fig. 12-7) as well as the Athena Promachos (i.e., a bronze statue of Athena) adjacent to the entrance of the Acropolis in Athens (Fig. 12-8). The influence of Pythagorean mathematics, the Kanon (i.e., the relationship of the parts to the whole), and the golden ratio (although not spoken of as a specific number) are clearly represented in all of Phidias’ works.

Figure 12-8 Statue of the Goddess Athena at the entrance of the Athenian Acropolis by Phidias. From http://en.wikipedia.org/wiki/File:NAMA_Ath%C3%A9na_Varvakeion.jpg Photograph by Marsyas. Creative Commons License: Attribution.
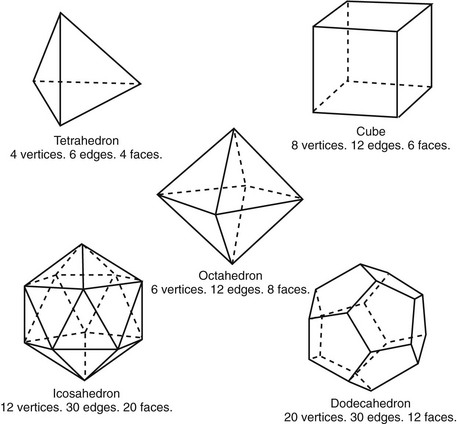
Pythagoras’ writings also influenced Plato (428 B.C.-337 B.C.), who is considered one of the most extraordinary minds of Ancient Greece and of Western civilization in general.100 His text, the Republic, states that mathematics is an absolute must for the education of all state leaders and philosophers (Fig. 12-9). Plato was intrigued by the five regular polyhedrons that are now considered the Platonic solids (Fig. 12-10). He used their design to emphasize the importance of proportions for the achievement of “ideal” beauty. His thinking must have also been greatly influenced by Polykleitos’ sculptures and written words in the Kanon. Plato is quoted as follows:
Two parts or values cannot be satisfactorily connected among themselves without a third part; the most beautiful link is that, which together with two initial values gives the perfect unit. It is reached in the best way by proportion [analogy], in which among three numbers, planes or bodies, the mean one so concerns to the second one, as the first one to the mean one, and also the second one to the mean one as the mean one to the first one. This implies, that the mean one can exchange the first one and the second one, the first one and the second one can exchange the mean one and all things together thus makes an indissolvable unit.61,100
Plato’s favored student Aristotle (384 B.C.-?) was able to take Pythagorean ideas and the Kanon of Polykleitos a step further forward when he wrote that the main requirements of beauty include order, proportionality, and control of sizes (i.e., the relationship of the parts to each other).100 Order was said to arise “when between parts of the whole there are definite ratios in proportions.”61,100 In music, for example, Aristotle recognized the octave as the most beautiful consonance when taking into consideration that the number of oscillations between the basic tone and the octave can be expressed by the first numbers of a natural series: 1 : 2. He also had the opinion that rhythmic relations of a poetic verse should be based on small numerical ratios to reach a beautiful impression.41 Like Plato, Aristotle believed that beauty was commensurate of the separate parts to the whole.
The young Alexander the Great of Macedonia (Fig. 12-11) succeeded to the throne after his father’s assassination (336 B.C.). He went on to conquer most of Asia Minor, Syria, Egypt, and Babylon, and he then founded the City of Alexandria near the mouth of the Nile. Alexandria developed into the intellectual center of the hemisphere, and it included a library that is said to have held more than 700,000 books. The first group of scholars at the center included the young Euclid (300 B.C.), who authored a complete text about the history of mathematics that included many of his own original ideas (Fig. 12-12). The Elements was a 13-volume work on geometry and number theory.43 Each book contained a number of theorems (i.e., from 10 to 100) that follow a series of definitions. Scholars believe that the Elements is primarily a collection of theorems described by other mathematicians that was then supplemented by at least some original work by Euclid. Proclus, a Greek mathematician who lived several centuries after Euclid, wrote the following in his commentary about the Elements: “Euclid, who put together the Elements, collecting many of Eudoxus’ theorems, perfecting many of Theaetetus, and also bringing to irrefutable demonstration the things which were only somewhat loosely proven by his predecessors.”5 For example, Pythagoras was probably the source of most of Books 1 and 2; the ideas of Hippocrates were found in Book 3, and those of Eudoxus were in Book 5; Books 4, 6, 11, and 12 probably came from other Pythagorean or Athenian mathematicians. Euclid is credited with replacing Fallacious’ proofs with his own more rigorous versions. Most of the definitions, postulates, and axioms within the Elements date back to Plato. Euclid also authored almost a dozen other books that covered topics from music to mechanics and optics. His book Optics contains some of the earliest studies of perspective. Interestingly, until the 20th century, Euclid’s Elements remained second only to the Bible with regard to the number of books sold worldwide. Euclid’s textbook, through various translations, has remained actively referenced for more than 2300 years.

Figure 12-11 Sculpture of Alexander the Great of Macedonia. From http://en.wikipedia.org/wiki.File:Alexander1256.jpg
The golden ratio or golden section appears in the Elements, primarily in relation to proportions in Book 6: On Divisions of Figures.43 Book 6 survives only partially in an Arabic translation, and it discusses the division of geometric figures into two or more parts or into parts in given ratios. It is likely that Euclid’s primary interest in the golden ratio was as a means of geometric interpretation of the construction of the five Platonic solids. This discussion is also found in Book 13, which constructs the five regular Platonic solids that are inscribed within a sphere. Euclid calculated the ratio of their edges to the radius of the sphere and proved that there are no other regular solids to be found. Curiosity about the structure and design of these Platonic Solids were of much interest to Ancient Greek intellectuals.47 In addition, throughout the Elements, Euclid described several theorems and their proofs, which also employed the golden ratio. Although no documentation has been found to confirm Euclid’s knowledge of Polykleitos’ Kanon or Aristotle’s stated requirements of beauty (i.e., order, proportionality, and control of sizes), it is almost inconceivable that these ideas did not influence him.
Marcus Vitruvius Polio (80 B.C.-15 B.C.) came two centuries after Euclid; he was a Roman writer, architect, and engineer. At one point, he even served as Chief of Artillery for the Roman Army. His written work De Architectura, a 10-volume treatise on architecture, is not just remarkable for its originality and contents but also for being the only surviving major book about architecture from classic antiquity (Fig. 12-13). This treatise indicates a mastery of architecture and engineering, and it crystallizes the importance of precise proportions as a fundamental component of beauty in the human form. Interestingly, in the records that remain, no mention is made by Vitruvius of Pythagoras, Polykleitos, or Euclid. This lack of acknowledgement by Vitruvius is striking in its absence; thus, it likely represents lost documents rather than a lack of awareness.
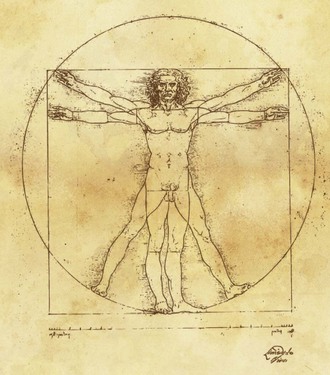
Fortunately, Vitruvius’ treatise would later be rediscovered by the Florentine humanist Poggio Bracciolini (1414). It was Leon Battista Alberti (1404-1472) who then revitalized Vitruvius’ works by writing a widely read seminal treatise on architecture, De Re Aedificatoria, which was published in 1450.35 During the High Italian Renaissance, this volume had a great influence on artists, scholars, and architects, including Leonardo da Vinci (1452-1519) and Michelangelo (1475-1564).72 Vitruvius is most remembered for his basic assertion that a structure must exhibit the three qualities of firmitas, utilitas, and venustas: it must be strong (durable), useful, and beautiful. According to Vitruvius, architecture is an imitation of nature: “As birds and bees built their nests, so humans construct housing, from natural materials that give them shelter against the elements.”61 When perfecting the art of building, ancient greeks designed and defined the three architectural orders: Doric (Fig. 12-14), Ionic (Fig. 12-15), and Corinthian (Fig. 12-16).100 These architectural orders gave the Ancient Greek buildings a sense of proportion and continuity that was believed to be as important as the proportions of the greatest known work of art: the human body. This led Vitruvius to define the proportions of the human body in words that would later be illustrated by Leonardo da Vinci’s Vitruvian Man (1437; Fig. 12-17). The human body as described by Vitruvius was inscribed in a circle and in a square. These are considered the fundamental geometric patterns of the cosmic order.102
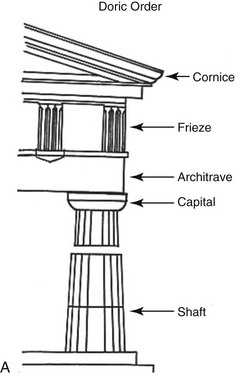

Figure 12-14 A, Illustrations of Doric architecture. B, Doric architecture as demonstrated by the Parthenon from Ancient Greece. Courtesy Charlotte-Mecklenburg Historic Landmarks Commission. http://www.cmhpf.org/kids/dictioary/classicalorders.html
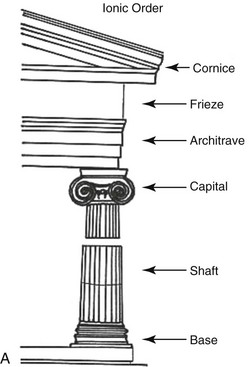

Figure 12-15 A, Illustrations of Ionic architecture. B, Ionic architecture as demonstrated by the Temple of Athena Nike from Ancient Greece. Courtesy Charlotte-Mecklenburg Historic Landmarks Commission. http://www.cmhpf.org/kids/dictioary/classicalorders.html
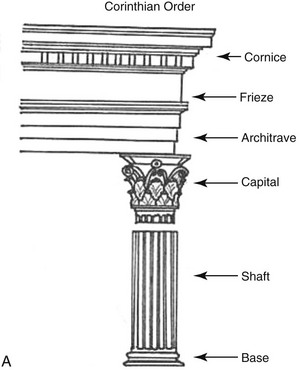

Figure 12-16 A, Illustrations of Corinthian architecture. B, Corinthian architecture as demonstrated by the Temple of the Sybil from Ancient Greece. Courtesy Charlotte-Mecklenburg Historic Landmarks Commission. http://www.cmhpf.org/kids/dictionary/classicalorders.html.
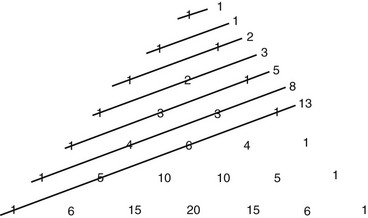
Abu Kmil’s books would later serve as a basis for Leonardo of Pisa’s further understanding of Euclid’s geometric principles. Leonardo of Pisa (1170-1250) was also known as Fibonacci, Leonardo Bonacci, Leonardo Pisano Bogollo, and Leonardo Fibonacci; he was considered the most talented mathematician of the late middle ages.25 He is best remembered by the modern world for spreading knowledge of the Hindu-Arabic numeral system (i.e., digits 0 through 9) in Europe; this was primarily done through publication during the earlier 13th century of the Book of Calculations or Liber Abaci.97 His second contribution was the recognition of a number sequence that became known as the Fibonacci numbers (Fig 12-18). Within the Liber Abaci, Fibonacci posed and solved a classic problem involving the growth of a hypothetical population of rabbits that was based on idealized assumptions (Fig 12-19). The solution was a sequence of numbers that was later named after Fibonacci. Although this number sequence was known to Indian mathematicians as early as the sixth century, it was Fibonacci’s Liber Abaci that introduced it to the West.101 In the sequence of the Fibonacci numbers, each number is the sum of the previous two numbers, starting with 0 and 1. Thus, the sequence begins 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on. Interestingly, the higher up in the sequence, the closer two consecutive numbers in the sequence—when divided by each other—will approach the golden ratio of approximately 1 : 1.618 or 0.618 : 1. The sequence of the Fibonacci numbers and their relative ratios have been found with consistency in nature, art, and classic objects of beauty. They would soon be recognized and used by the Renaissance painters.
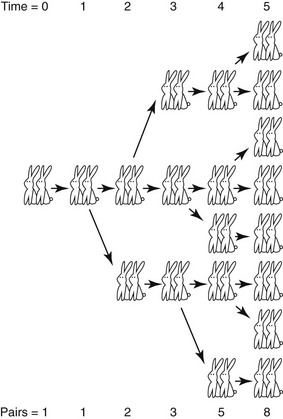
Figure 12-19 Fibonacci numbers as described through breeding rabbits. The sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, and so on—in which each term (starting with the third) is equal to the sum of the two preceding terms—was appropriately dubbed the Fibonacci numbers during the 19th century by the French mathematician Edouard Lucas (1842-1891).
The Fibonacci numbers and the golden ratio are found in the most basic forms in nature.25 For example, spirals arise from a property of growth called “self-similarity” (i.e., the tendency to grow in size but to maintain the same shape). This is seen in the simplest of natural forms: the shell of the chambered nautilus. As the nautilus outgrows each chamber, it builds a new chamber for itself, but this always has the same shape (Fig. 12-20). If the nautilus lives a long life, it will spiral around and around, growing even larger but always looking exactly the same at every scale. Interestingly, by using the Fibonacci sequence of numbers, you can build a nautilus that is based on squares by starting with a square of size 1 and successively building new “rooms” with sizes that correspond with the Fibonacci sequence.39 Running through the centers of the squares, a smooth curve can be drawn that corresponds to the nautilus spiral (see Fig. 12-20, B). This self-similar curve, which keeps its shape at every scale, is called equiangular because a radial line from the center always makes the same angle to the curve. This curve was also known to Archimedes of Ancient Greece, who—philosophically and religiously—thought of this curve as both spiraling inward forever as well as spiraling outward forever. Euclid’s golden ratio mathematically describes this finding both in nature and in the Fibonacci numbers.
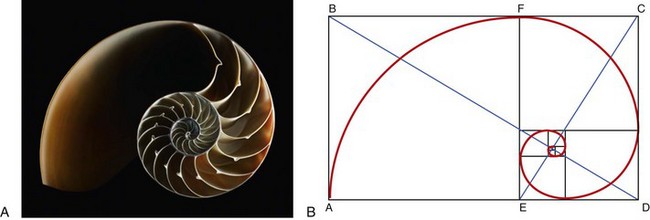
Figure 12-20 A, Photograph of the chambered nautilus, which demonstrates structural anatomy. B, The golden ratio as found in the spiral structural anatomy of the nautilus.
Euclid’s ideas have had an enormous impact throughout the centuries,5 first on the medieval Italian philosopher St. Thomas Aquinas (1225-1274) and then on the Renaissance Italian architect L.B. Alberti (1404-1472).72 Aquinas captured the fundamental relationship between beauty and mathematics when he stated that “humans seem to react with a sense of pleasure to forms that possess certain symmetries [proportions] and obey certain mathematical rules.”35,61
Leon Battista Alberti was an author, artist, architecture, poet, priest, linguist, philosopher, cryptographer, and general Renaissance humanist. Alberti regarded mathematics (as summarized by Euclid) to be the common ground of the arts and the sciences. For Alberti, beauty was “the harmony of all parts in relation to one another.” He stated that “this concord is realized in a particular number, proportion and arrangement demanded by harmony.”35,61 Alberti’s thoughts on harmony were referenced back to Pythagoras and Euclid, but he set them in a fresh context. He studied Ancient Roman sites, ruins, and objects and made detailed observations that are cataloged in his Ten Books of Architecture (De Re Aedificatoria), which was published in 1450 A.D. His writings were patterned after the De Architectura by Vitruvius (46 B.C.-30 B.C.) and covered a wide range of subjects, from history to town planning to engineering to the philosophy of beauty.
Three Renaissance genius mathematicians and artists were clearly influenced by Euclid’s ideas72: Piero della Francesca (1415-1492), Leonardo da Vinci (1452-1519), and Luca Pacioli (1446-1517). Piero della Francesca was known as a mathematician, a geometer, and an artist. His painting was characterized by its serene humanism and its use of geometric forms, particularly in relation to perspective and foreshortening (Fig. 12-21). It is known that he was at least acquainted with Leon Battista Alberti’s mathematical and architectural work and that he would also have a significant influence on Luca Pacioli’s thinking.71 Three important mathematical treatises were written by Piero: Abacus Treatise (Trattato d’Abaco); Short Book on the Five Regular Solids (Libellius de Quinque Corporibus Regularibus); and Perspective on Painting (De Prospectiva Pingendi). The subjects covered in these writings include mathematics, algebra, geometry, and innovative work on both solid geometry and perspective. Much of Piero’s work would later be rewritten by others, including Luca Pacioli.71 Piero’s work on solid geometry appears in Pacioli’s De Divina Proportione, which is believed to have been illustrated by Leonardo da Vinci. Piero’s Perspective on Painting (De Prospectiva Pingendi) clearly refers to Euclid’s Elements and Optics. Piero used Euclid’s written works to demonstrate that, to achieve perspective in a painting, the artist must rely on the scientific basis of visual perception. Piero’s treatise De Prospectiva Pingendi became the standard manual of the day for artists who attempted to paint plain figures and solids.
Luca Pacioli (Fra Luca Bartolomeo de Pacioli) lived from 1446 to 1517. He was a Franciscan friar and an Italian mathematician.71 He later collaborated with Leonardo da Vinci, and he also made seminal contributions to the field that is now known as accounting. In 1494, his first book—Summa di Aritmetica, Geometria, Proporzioni e Proporzionalità was published in Venice. This text compiled the knowledge of the time related to arithmetic, algebra, geometry, and trigonometry. Pacioli identified Fibonacci (Leonardo of Pisa) as the primary source for his basic facts. Several years later, he met, collaborated with, lived with, and taught mathematics to Leonardo da Vinci. Pacioli also completed the three-volume treatise The Divine Proportion (De Divina Proportione), which applies to geometrical proportions, letters, and architecture constructions. The original manuscript, which was written around 1496 to 1498, is preserved in Milan; it was published in Venice in 1509.71 Within the text, Pacioli lists five reasons why a more appropriate name for Euclid’s golden ratio would be “the divine proportion.” References and analogies to the church and godliness clarify Pacioli’s belief that the divine proportion is spiritual and universal. He was also interested in the process of painting, and he emphasized his desire to reveal the secret to the creation of harmonic forms through the use of the golden ratio (or the divine proportion). Pacioli used the square and the compass (which are clearly visible in the background of his well-known self-portrait) to both analyze the works of others and to help artists achieve divine proportions in their paintings (Fig. 12-22). It is believed that Pacioli invited Leonardo da Vinci to provide 60 illustrations, primarily of solid objects, to clarify the importance of the divine proportion. (Fig. 12-23). Leonardo’s drawings are the first illustrations of geometric figures in the dual state of skeletonic (vacuum) and solid (solidum) (Fig. 12-24). This allowed for a distinct interpretation between front and back. Pacioli wrote of da Vinci’s contributions to society by stating that “he is the most excellent painter in perspective, architect, musician and man endowed with all virtues.”71 Pacioli’s text largely restates the earlier published work of the Roman architect Marcus Vitruvius Polio.5 Within the text, Pacioli states the following:
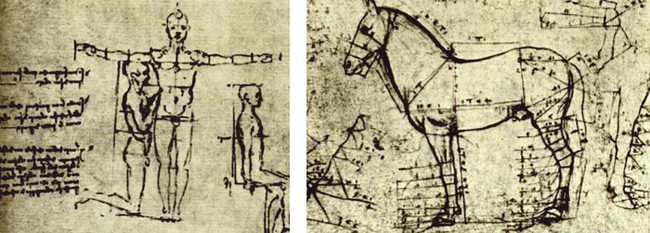
Figure 12-23 Drawings by Leonardo da Vinci confirming the golden ratio found in humans and other mammals. From Royal Collection Trust/©Her Majesty Queen Elizabeth II 2013.

Figure 12-24 Virgin of the Rocks by Leonardo da Vinci, confirming the golden ratio. From Stamperia d’Arte Fratelli Alinari. Bibliotecca Reale, Turin, Italy. Photo Credit: Alinari/Art Resource, NY.
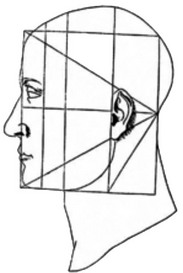
It is clear from a woodcut sketch included in De Divina Proportione (1509) that Luca Pacioli understood the importance of the golden ratio as it applies to the human face (Fig. 12-25). It is also believed that, at the request of Pacioli, Leonardo da Vinci took Vitruvius’ written words and drew them out in a diagram that he called Vitruvian Man (1487; see Fig 12-17).61 The image depicts a male figure in two superimposed positions with his arms and legs apart and simultaneously inscribed in a circle and a square. The illustrated interpretation of Vitruvius’ words is sometimes also called the Canon of Proportions; the original drawing is stored in the Galleria dell’Accademia in Venice, Italy. It is known that Vitruvius described the human figure as being the principal source of correct proportions and symmetry among the classic orders of architecture. da Vinci’s Vitruvian Man beautifully demonstrates the blend of art and science envisioned by intellectuals during the renaissance, and it provides a clear understanding of the artist’s keen interest in the proportions of the human form. Like Plato, da Vinci believed the workings of the human body to be an analogy of the workings of the universe. According to Leonardo himself, in a note that accompanied the drawing, “it was made as a study of the proportions of the male human body as described by Vitruvius” (“Palmus autem habet quattuor digitos”).61,72 Vitruvius’ words, which Leonardo attempted to draw out in pen and ink on paper, are found in Vitruvius’ De Architectura 3.1.2-3, which reads as follows:
For the human body is so designed by nature that the face, from the chin to the top of the forehead and the lowest roots of the hair, is a tenth part of the whole height; the open hand from the wrist to the tip of the middle finger is just the same; the head from the chin to the crown is an eighth, and with the neck and shoulder from the top of the breasts to the lowest roots of the hair is a sixth; from the middle of the breasts to the summit of the crown is a fourth. If we take the height of the face itself, the distance from the bottom of the chin to the underside of the nostrils is one-third of it; the nose from the underside of the nostrils to a line between the eyebrows is the same; from there to the lowest roots of the hair is also a third, comprising the forehead. The length of the foot is one-sixth of the height of the body; of the forearm, one-fourth; and the breadth of the breasts is also one-fourth. The other members, too, have their own symmetrical proportions, and it was by employing them that the famous painters and sculptors of antiquity attained to great and endless renown. Similarly, in the members of a temple, there ought to be the greatest harmony in the symmetrical relations of the different parts to the general magnitude of the whole. Then again, in the human body, the central point is naturally the navel. For if a man is placed flat on his back, with his hands and feet extended, and a pair of compasses centered at the navel, the fingers and the toes of his two hands and feet will touch the circumference of a circle described therefrom. Just as the human body yields a circular outline, so too a square figure may be found from it. For if we measure the distance from the soles of the feet to the top of the head, and then apply that measure to the outstretched arms, the breadth will be found to be the same as the height, as in the case of plain surfaces which are perfectly squared.61,72
For some scholars and artists of the High Italian Renaissance, the golden ratio was elevated from a simple mathematical formula to become a way of explaining natural phenomena and a tool to be used in the painting of objects and human forms.66,93 By the mid 1400s, advances in technology allowed artists to use lenses, concave mirrors, and other methods to help them to create realistic-looking paintings. Many of today’s critics believe that, simply by using their innate aesthetic sense, talented artists, architects and designers of that time period created art, built structures, and designed objects that closely approximate the golden ratio.46 Skeptics often claim that the most attractive and harmonious objects were methodically designed by their artists to adhere to the golden ratio measurements; they also believe that many of the great artists’ designs were simply superimposed on laid-out golden ratios. Interestingly, many other scholars deny that the Greeks (e.g., Euclid) made any direct aesthetic associations with the golden ratio. Thus, some questions remain unanswered: Throughout antiquity and during the Renaissance, did artists consciously use the golden ratio as part of their technique? Did they model their work on precise mathematical dimensions, or was their aesthetic and artistic sense the guiding force that inevitably closely approximated the golden ratio?
The analysis of Leonardo’s drawing entitled A Head of an Old Man (Fig. 12-26) leaves little doubt that he was, at the very least, intrigued by various proportions of the face. This drawing shows how Leonardo used standard rectangles to determine dimensions in his paintings. Because classic art requires “harmony” and because we know that Leonardo collaborated with Pacioli and that he was believed to be the illustrator of Divine Proportions, Leonardo’s use of the golden ratio in his paintings would be an obvious extension of his mathematic knowledge and artistic principles. Most of today’s art critics place Leonardo’s Mona Lisa on a short list of the most beautiful faces ever painted (Fig. 12-27). Debate continues regarding Leonardo’s conscious use of the golden ratio in this well-known work. Interestingly, da Vinci is said to have revised the Mona Lisa for more than 10 years before his death without ever fully finishing the work to his own satisfaction.
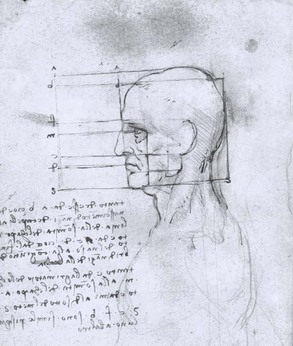
Figure 12-26 Head of an Old Man by Leonard da Vinci, confirming the golden ratio. From Royal Library, Windsor Castle, Windsor, Great Britain. Photo Credit: Alinari/Art Resource, NY.
After Leonardo, the golden ratio as an artistic principle likely fell from favor. To my knowledge, no prominent philosopher or artist was known to have actively used the golden ratio again until Adolf Zeising (1810-1876).105 Zeising was formally trained in psychology, mathematics, and philosophy. He found the golden ratio expressed in all things, including in the skeletons of animals and the branching of their veins and nerves (Fig. 12-28). In connection with his theory involving golden-ratio–based human body proportions, Zeising (1854) wrote what he called the “universal law of proportions,” “in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form.”34
The famous German psychologist, Gustav Fechner, was inspired by Adolf Zeising’s book Der Goldene Schnitt and began a series of inquiries to see if the golden rectangle had psychological aesthetic impact.34 A golden rectangle is one with side lengths that reflect the golden ratio. A distinctive feature of this shape is that, when a square section is removed, the remainder creates another golden rectangle. In other words, it has the same proportions as the first. Another section can be removed infinitely, with the same results. Fechner’s work was published in 1876. He made thousands of measurements of commonly seen rectangles (e.g., writing pads, books, playing cards, windows) and found that most were close to phi (Fig. 12-29). He also tested people’s preferences and found that most people prefer the shape of the golden rectangle. Fechner’s experiments were repeated and validated by others, including Witmar (1894), Lalo (1908), and Thorndike (1917).34
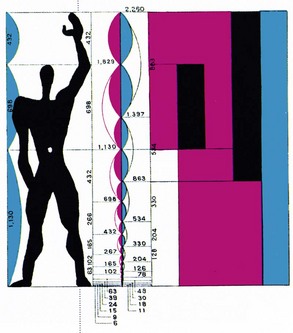
By the late 1800s, knowledge of and the conscious use of the golden ratio by painters, architects, and designers was well documented.34 There are clear examples where these professionals have modeled their end products to conform with Euclid’s golden ratio. In 1946 in The Geometry of Art and Life, Matila Ghyka presented an analysis of the face of the tennis champion Helen Wills.34 He made several measurements of Wills’ face, all of which were shown to be consistent with the divine proportion (Fig. 12-30). More recent examples include Salvador Dali’s use of the golden ratio in his masterpiece The Sacrament of the Last Supper (1955; Fig. 12-31) and the experimental piece of music Binary Universe (2006) by Brian Transeau. A strong advocate for the conscious application of the golden ratio to art, the design of objects, and architecture was Le Corbusier (1887-1965).32,59 His legacy remains one of the most influential in modern architecture. He developed an intense interest in proportional systems and their role in all forms of aesthetics. Le Corbusier’s fascination with the importance of the golden ratio in aesthetics centered around his belief that basic forms and structures are the underpinning of natural phenomenon. He developed what he called the Modulor in the tradition of Vitruvius with the intention of improving both the appearance and function of all manmade objects and architecture (Fig. 12-32).59 He was also a strong believer in the idea that ideal harmony in music (as stated by Pythagoras) could only be achieved through the application of the golden ratio to numbers.

Figure 12-30 Facial proportions of Helen Wills by Matila Ghyk, confirming the golden ratio. From Matila Ghyk: The Geometry of Art and Life, 1946, Kessinger Publishing, Oct. 30, 2004, p. 102.
Current Philosophy
From Pythagoras, Polykleitos, Plato, Aristotle, Euclid, Vitruvius, Galen, Fibonacci, Piero, da Vinci, and Pacioli as well as the more recent Le Corbusier and all of their disciples for more than 2.5 millennia, we have learned that the proportions of the parts to the whole affect the observers’ impression of beauty and attractiveness.1,3,7,23,26,29,36,56,62,82,96 From the premier artists, architects, and designers throughout the centuries, we know that mirror-image symmetry and the harmony of proportions matter when judging facial aesthetics. They have also shown by example that the precise—even to the millimeter—achievement of an exacting mathematical ratio is not sufficient or even preferred for the creation of the most important end products; rather, an approximation of the golden ratio is.
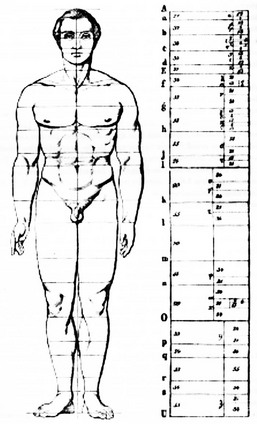
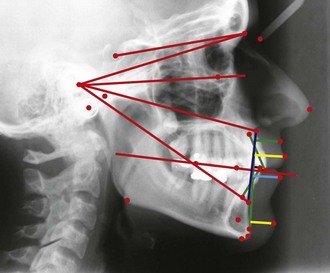
In the realm of facial aesthetics and reconstructive surgery, clinicians from all involved fields have from time to time attempted to match facial aesthetics to a strict mathematical model (e.g., normative cephalometric measurements) without always considering individual biologic variations and aesthetic nuances* (Fig. 12-33). When doing so, they have often fallen short of their objective. In 1984, Ricketts reported about a significant number of golden proportions when analyzing the facial skeleton and overlying soft tissues.83–91 He was a strong advocate of the use of these divine proportions as a guide for planning the correction of dentofacial deformities via orthognathic surgery (Fig. 12-34). The validity of Ricketts’ approach to facial analysis for the correction of jaw deformities has been questioned by some while supported by most.8,12,15,30,50,73,74,75,76,94 For the clinician who is asked to correct a congenital or developmental craniofacial or maxillofacial deformity, attention is directed to both form and function. As R. Buckminster Fuller stated, “rarely are the two objectives divergent.”61 For the achievement of a harmonious face, attention is directed toward the practical objectives of improving the upper airway and the occlusion, which will affect speech, swallowing, chewing, and breathing. Facial aesthetic perfection is not a specific millimeter distance or degree of angulation but rather a visual impression at conversational distance in three-dimensional life. At the same time, neither divine proportions nor biologic realities and the patient’s personal preferences can be ignored throughout the process.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses