Physical properties
Introduction
The uses to which dental materials are put are not conducive to mass production, as each patient is different from the last, and the material has to be specially moulded each time. As a consequence, most materials used by the dentist and the dental technician require some form of processing before they are hardened.
This processing often involves mixing the materials with others to produce a dough or liquid that can then be placed and shaped to suit the patient’s needs. The successful use of dental materials, therefore, requires some understanding of the way in which materials flow when they are mixed, poured or moulded. The study of the flow of materials is known as rheology.
When a patient drinks a cup of tea or eats an ice cream, the temperature in the mouth can range from 5 to 60°C. This can result in temperature differences within the tooth that can be quite pronounced. The pulp of the tooth would react severely if it were not protected from these temperatures, which differ greatly from the norm of 37°C. When a filling, crown, bridge or denture is placed, account must be taken of the need to protect the pulp from extremes of temperature. Therefore, the thermal properties of the dental materials need to be considered.
The restoration of the human dentition has moved more and more from the purely functional towards the aesthetic. Most patients now demand a level of restoration where it is virtually impossible to detect the fact that the dentist has intervened. Consequently, the optical properties of the materials that are selected and used by the dentist have become of great importance.
Rheological properties
Rheology is the study of the flow of materials. For liquids, flow is measured by the viscosity, whereas for solids one considers creep and viscoelasticity. Creep has already been described in the previous section and only the viscosity and the viscoelasticity will be considered here.
Viscosity
When a substance flows under the influence of an external force (e.g. gravity), the molecules or atoms come into contact with different neighbours. Thus, bonds must be broken and remade, and this gives rise to a resistance to flow, known as viscosity.
For a liquid such as water, the forces binding the molecules together are very weak and easily overcome, so the water flows quite readily and has a low viscosity. For some fluids, the intermolecular attractions are much stronger. This is usually associated with large molecules, such as in the case of treacle. The molecules may even become tangled up in one another, giving rise to very high viscosities. This is what happens with high-molecular-weight polymers.
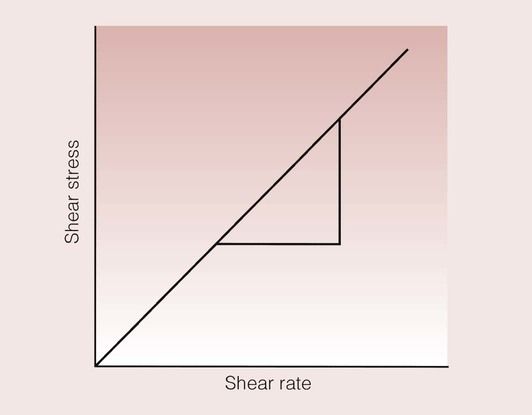
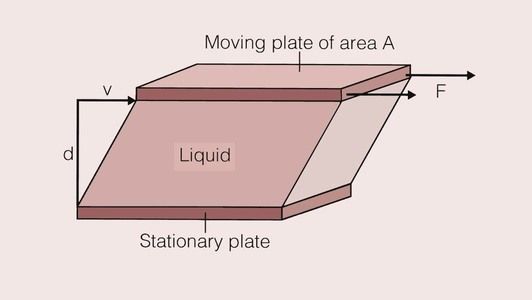
When we stir a liquid, we are effectively applying a shear stress, and the degree of vigour with which we stir it can be quantified by the shear rate. Such a situation is shown in Figure 1.7.1. The shear stress and the shear rate are defined by:
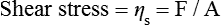
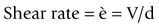
A number of methods are available for measuring the shear stress over a range of shear rates for a fluid, and the information collected can be plotted as a shear stress–shear rate curve. This relationship is linear for many fluids, and a typical curve for such a fluid is shown in Figure 1.7.2. The slope of the curve is equal to the viscosity, so that the exact scientific definition of viscosity, η, is given by:
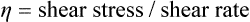
The units of viscosity are Pascal seconds (Pa.s).
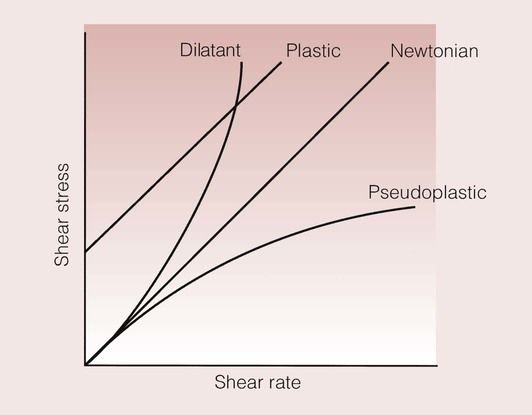
The viscous properties of substances that have a linear relationship between shear stress and shear rate are given entirely by this single value of viscosity, and are said to be ‘Newtonian’ in behaviour.
However, not all materials behave in this simple fashion, and some of the different forms of behaviour are shown in Figure 1.7.3.
Liquids with plastic behaviour will not flow until an initial shear stress has been reached. The fluid will then flow in a Newtonian fashion.
Dilatant liquids show an increase in viscosity as the shear rate goes up. This means that the faster one tries to mix the fluid, the more difficult the liquid becomes to mix. It is not possible to define the flow characteristics of such a liquid by a single viscosity.
For some liquids, an increase in shear rate does not lead to a corresponding increase in shear stress. This means that the liquid becomes easier to mix at higher shear rates than would be the case for a Newtonian or dilatant liquid. This behaviour is described as pseudoplastic, and leads to the feature of some liquids that is commonly known as shear thinning. A dental example of this type of behaviour is in silicone impression materials, where shear thinning makes the flow of the fluid from a syringe much easier than it would otherwise have been.
Thixotropy
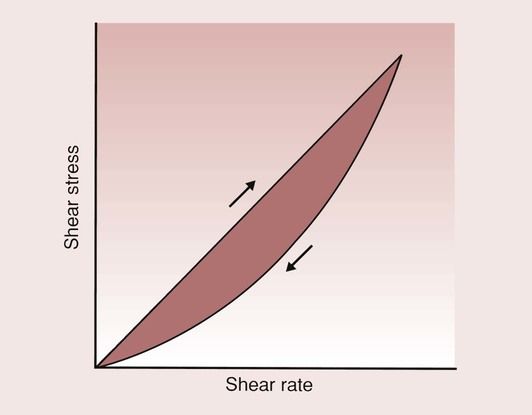
So far, it has been assumed that the viscosity can be determined from a knowledge of the shear stress and shear rate at any one instant in time. For some substances, the viscosity will change at a particular shear rate, and if one plotted the shear stress against the shear rate for such a liquid, one would typically find the response shown in Figure 1.7.4.
In this case, the viscosity for an increasing shear rate is different from the viscosity for a decreasing shear rate, which is an example of hysteresis. In such cases, the viscosity of the fluid is dependent on the previous deformations to which the fluid has been subjected.
This type of behaviour occurs when there is some molecular rearrangement caused by the mixing, and a lack of time for the molecules to return to their normal arrangement before mixing again. The effect of this is that the longer the fluid is mixed at a given shear rate, the lower the shear stress and hence the viscosity will be. If the fluid were left for long enough, it would recover and the whole process could be repeated. This type of behaviour is defined as thixotropic, and one fluid that exhibits this is non-drip paint.
Viscoelasticity
A wide range of materials show behaviour that is intermediate between that of a viscous liquid and that of an elastic solid. For an elastic solid, it has been assumed that the relationship between stress and strain is independent of any dynamic factors such as loading rate or strain rate. However, if given sufficient time to do so, some solids show a capacity to rearrange their molecules under the influence of an applied load, and this is reflected in a change in the strain. When the load is then released, the material does not immediately return to its original state. This means that the behaviour of the material is dependent on such factors as the duration and the amount of load applied.
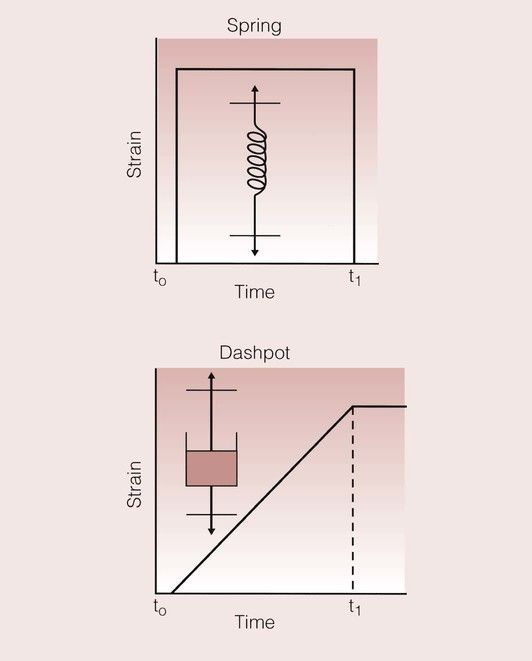
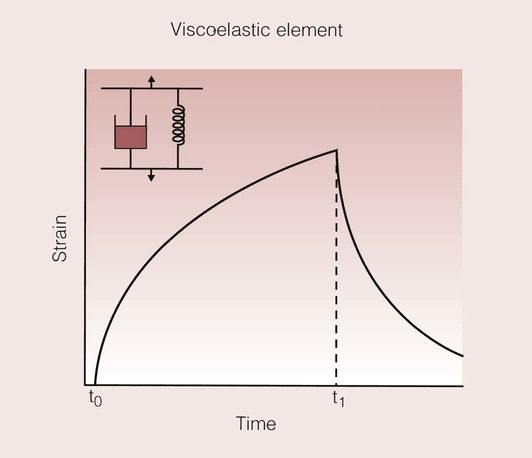
A simple and effective way of visualizing this problem is through the use of models based on a spring and a dashpot, which combine to give a system rather like a shock absorber. The spring represents the elastic element, and the dashpot represents the viscous element. The variation of the strain with time for these models is shown in Figure 1.7.5. For the spring, the application of a load results in an immediate strain that is maintained for as long as the load is applied. Once the load is removed, the spring returns instantaneously to its original state. In contrast, on the application of a load to the dashpot, there is a gradual increase in the strain, which continues to increase for as long as the load is applied. On removal of the load, the strain is not relieved, and the dashpot remains in its new position.
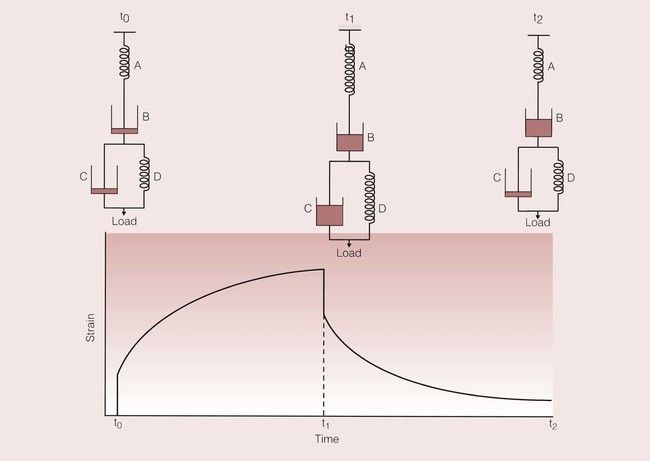
When these two elements are placed in parallel, a simple viscoelastic model is created. The strain response for such a model is shown in Figure 1.7.6. In this model, the dashpot prevents the spring from responding elastically. Now, the dashpot gradually lets the spring approach its desired strained state. On removal of the load, the dashpot prevents the spring contracting to its unstrained state, which it can now only achieve after some time.
A dental example of a group of materials that show viscoelastic behaviour would be that of the elastomeric impression materials. The strain–time curve for such a material, and the corresponding model based on the elastic, viscous and viscoelastic elements are shown in Figure 1.7.7.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses