Introduction

When one stretches a steel wire or a rubber band, the responses of the materials are quite different. The steel wire will hardly appear to change; although it will become longer, this change is normally so small that it is difficult to perceive. On the other hand, the rubber band will stretch quite readily, and can virtually double in length. Obviously, different materials respond quite differently to the application of a load.

We could make a component and determine its response to an external loading. However, the data collected would be applicable only to that component, and would not allow us to predict the behaviour of a differently shaped component that was made from the same material.

How are we to compare the performances of materials in different applications? Obviously, we need some objective standard of comparison that is independent of the size and shape of the material. Once we have such a standard, it should be possible to compare the properties of different materials, and to predict the behaviour of objects made from them.

The bases for such an objective standard are the quantities called stress and strain. The description of the mechanical properties of materials is based on these, so we shall now consider them in some detail.

Stress and strain

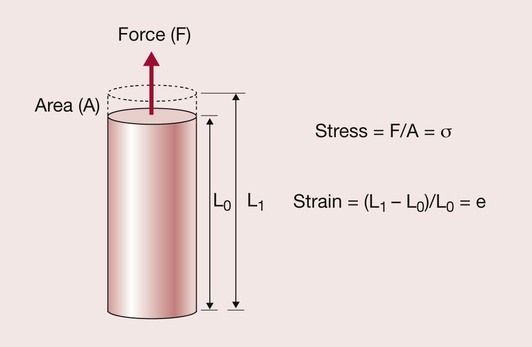
The simplest approach to understanding stress and strain is to consider a rod of material that is held under tension by being subjected to a tensile force, or load. As shown in Figure 1.6.1, the rod will extend.

Naturally, one would expect the rod to fail (i.e. to snap or to deform irreversibly) under a high enough load. The load at which failure occurs is a measure of the strength of the rod, but it is particular to a rod of those specific dimensions and specific material. The load that the rod could bear without failing would be increased if the diameter of the rod was increased, and would decrease if the diameter were decreased.

The amount of extension of the rod at the time of failure depends on the starting length of the rod, such that the longer the starting length, the greater the extension. Thus, force and extension do not represent the ideal means of defining the mechanical properties of a material.

The way to overcome the dependence on the dimensions of the rod is to introduce the parameters of stress, σ, and strain, e, for the material under test.

The definitions for these parameters are:

Thus, if a rod is subjected to a tensile force, F, along its length, the stress, σ, is given by:

σ=F/A

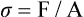
where A is the cross-sectional area of the rod. The units used to measure stress are Newtons per metre squared (N·m⁻² = Pascal = Pa).

At the same time as when the force is applied, the rod’s length changes from its original length L₀, to the extended length L₁. The strain that results, e, is given by:

e=L1−L0/L0

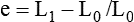
This parameter is dimensionless, as it involves the calculation of length divided by a length.

In practice, we can measure the load–extension curve for a material, and then convert this to a stress–strain curve. Once we have this information, it is possible to predict the load–extension curve for a rod of any cross-sectional area and length. We can also compare the response of different materials to the same tensile force.

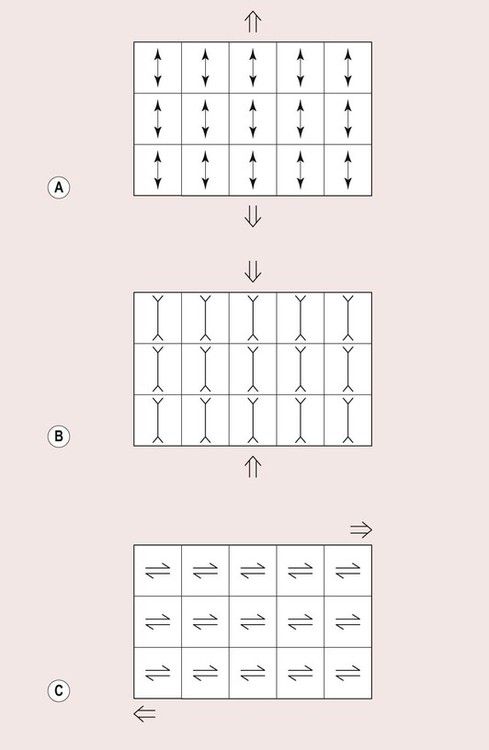
Stress and strain are not properties in themselves, but allow the definition of a number of mechanical properties that could not be defined otherwise. In the example described above, the stress was generated by a load applied in an axial direction (i.e. along the rod), but in practice, a load could be applied in any direction, and in most situations there will be more than one load involved. These loads give rise to complex stress patterns in the structure.

The three principal types of stress are tensile stress, compressive stress and shear stress, and these are shown schematically in Figure 1.6.2.

Definitions of some mechanical properties

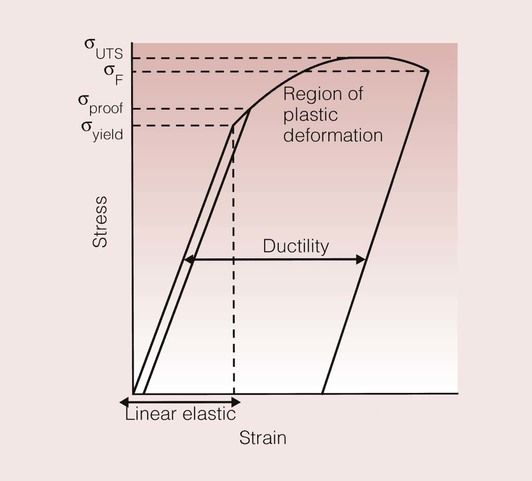
A typical stress–strain curve for a metal such as a brass alloy is shown in Figure 1.6.3. It can be used to identify several of a material’s properties.

Elastic limit and plastic flow

An important feature of the mechanical behaviour of materials is the relationship between the stress and the strain. Immediately noticeable in Figure 1.6.3 is the fact that this brass alloy does not show a linear relationship between stress and strain along the full length of the curve.

The region where the stress–strain curve is linear is known as the linear elastic region, and represents the range where elastic deformation occurs. In this region, removal of the stress from the material results in the material returning to its original shape.

Where the curve begins to deviate from its linear path, the material will have exceeded its elastic limit and will begin to deform permanently; removal of the stress from the material does not result in the return of the material to its original shape. This is known as plastic flow, and is represented by the region of plastic deformation on the graph.

Young’s modulus

When a material is stressed, it is usually found that the stress is initially proportional to the strain, so their ratio is constant. In other words, the material deforms linearly and elastically. This can be represented by the expression:

σ/e=E

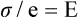
which allows us to define another property of the material: namely, the Young’s modulus, denoted by E. Young’s modulus is the constant that relates the stress and the strain in the linear elastic region, and is a measure of the stiffness of the material.

Note that the stiffness of a rod is dependent on its shape and dimensions, and on the Young’s modulus of the material from which it is constructed. Once we know the Young’s modulus of a material, it is possible to determine the stiffness of any structure made from that material.

Since Young’s modulus is obtained by dividing the stress by the strain, the units are the same as those of stress (N·m⁻²). The value of Young’s modulus is often very large for real materials. To make the values more manageable, it is usual to express the value of Young’s modulus in Gigapascals (GPa), where 1 Pascal is 1 N·m⁻², and 1 Gigapascal is 10⁹ N·m⁻².

The Young’s modulus is often described as simply the elastic modulus, or the modulus of elasticity.

Fracture strength

It is now possible to define the fracture strength of the material, σ_f, since this is simply the stress required to break it.

Only gold members can continue reading. Log In or Register to continue