In the previous article, I discussed 1-way analysis of variance (ANOVA) when we are interested in comparing the generated forces from 3 types of wires. In that example, we considered only 1 factor, which was the type of wire. If we want to compare simultaneously the effect of 2 factors on the outcome of interest, then we can use 2-way ANOVA. The 2 independent variables in a 2-way ANOVA are called factors, indicating 2 variables that affect the dependent variable, and each factor has 2 or more levels in it. There are 3 sets of hypotheses with the 2-way ANOVA.
- 1.
The sample means across the levels of the first factor are equal, just like the 1-way ANOVA (row factor).
- 2.
The sample means across the levels of the second factor are equal, just like the 1-way ANOVA (column factor).
- 3.
There is no interaction between the 2 factors. No interaction means that the first factor affects the dependent variable on average similarly in each level of the second factor, and vice versa.
The first 2 hypotheses assess the main effects. The main effects involve the independent variables one at a time, ignoring any interaction. Just the rows or just the columns are used; this part is similar to the 1-way ANOVA. The third hypothesis assesses the interaction effect: ie, the effect of one factor on the other factor.
Example
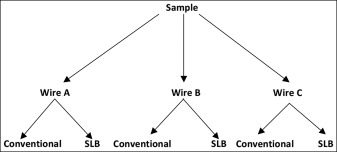
Research question: Compare the forces generated (continuous outcome) for the 3 types of wires, A, B, and C, and also account for another parameter such as type of bracket—conventional or self-ligating. We can make this assessment by using 2-way ANOVA, since we have 2 factors: wire type (3 levels: A, B, and C) and bracket type (2 levels: labial and lingual). This design is a 3 × 2 factorial design, and it is efficient, in the absence of interaction, because it allows testing of 2 factors in a study by using the same sample size.
The Figure is a diagrammatic presentation of the 3 × 2 factorial design to assess simultaneously the effect of wire type and bracket mesh type on the generated forces.