The molecular environment
Publisher Summary
This chapter focuses on the molecular environment. Life is essentially a watery affair. Its aquatic origins are reflected in the high water contents of the cells and tissues even of terrestrial plants and animals. Mammalian cells contain some 70–75% of water, while soft tissues range from 65 to 80% in water content. Considering extremes, whole blood contains about 80% of water, while heavily mineralized compact bone may have only 15%. The lowest content is reached in dental enamel that, when mature, contains only 4% by weight of water. A man weighing 65 kg contains about 40 kg or liters of water of which 25 kg are within cells and 15 kg are extracellular. Water provides an all-pervading environment that surrounds and interacts with the whole gamut of biological molecules, small and large. Most biochemical reactions take place within or near this aqueous continuum; their very occurrence often depends upon the presence and special nature of water. Although water is commonplace and familiar, its apparent simplicity is deceptive.
The biological ubiquity of water
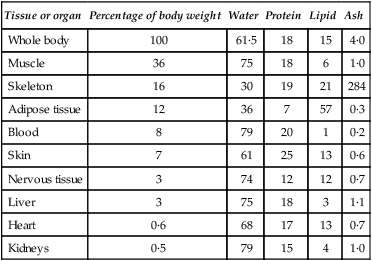
Life is essentially a watery affair. Its aquatic origins are reflected in the high water contents of the cells and tissues even of terrestrial plants and animals. Mammalian cells contain some 70–75% of water, while soft tissues range from 65 to 80% in water content. Considering extremes, whole blood contains about 80% of water while heavily mineralized compact bone may have only 15%. The lowest content is reached in dental enamel which, when mature, contains only 4% by weight (approximately 10% by volume) of water. A man weighing 65 kg contains about 40 kg (or litres) of water (i.e. 62%) of which 25 kg are within cells and 15 kg are extracellular. Water in the plasma accounts for only 3 kg the remaining 12 kg of extracellular water being interstitial and bathing the cells within the tissues. The approximate composition of the body is given in Table 3.1.
Table 3.1
Approximate values for the chemical composition of the adult human body
| Tissue or organ | Percentage of body weight | Water | Protein | Lipid | Ash |
| Whole body | 100 | 61·5 | 18 | 15 | 4·0 |
| Muscle | 36 | 75 | 18 | 6 | 1·0 |
| Skeleton | 16 | 30 | 19 | 21 | 284 |
| Adipose tissue | 12 | 36 | 7 | 57 | 0·3 |
| Blood | 8 | 79 | 20 | 1 | 0·2 |
| Skin | 7 | 61 | 25 | 13 | 0·6 |
| Nervous tissue | 3 | 74 | 12 | 12 | 0·7 |
| Liver | 3 | 75 | 18 | 3 | 1·1 |
| Heart | 0·6 | 68 | 17 | 13 | 0·7 |
| Kidneys | 0·5 | 79 | 15 | 4 | 1·0 |
The structure and properties of water
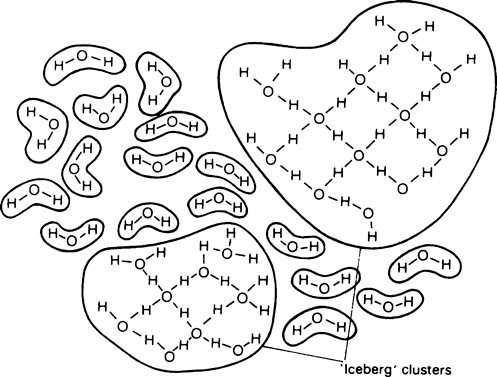
When ice melts, its continuous crystalline structure is partially broken down and becomes more complex. Water consists partly of free molecules and partly of ‘clusters’ or ‘icebergs’ in which a number of molecules are joined together by hydrogen bonds (Figure 3.1).
Interaction between water and biological molecules
As a result of interaction between water and organic substances including proteins, the structure of the water at the interface is modified (page 55) so that it differs from the structure of bulk water. This interaction may also modify the structure of the organic molecules. Consequently not only do biological molecules themselves take on a preferred configuration but they become surrounded by layers of water which behave in a different manner from the bulk of free water. Almost all of the large amount of water present in living cells is in the form of orientated multi-layers on the surfaces of cell proteins and the special properties of orientated water are intimately concerned with the chemical changes that are the basis of life.
Water as an ionizing solvent
Water is a good solvent for a variety of inorganic substances and also for many organic substances except for those that are predominantly hydrocarbon in nature. The specific solvent properties of water arise from its highly polar character and unequal charge distribution, which result from an excess of electrons near the oxygen atom and a deficiency near the hydrogen atoms. The molecule thus acts like a small dipole with its negative charge near the oxygen and its positive charge midway between the two hydrogen–oxygen bonds (page 14).
When salts dissolve in water they are almost completely dissociated into ions, e.g.
< ?xml:namespace prefix = "mml" />
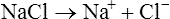
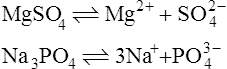
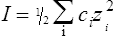
Hydrogen ions and the idea of acidity
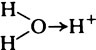
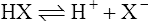 (3·1)
(3·1)Different acids vary considerably in their strength. A strong acid is one that gives up protons readily whereas a weak acid gives them up reluctantly. A strong base acquires protons avidly and a weak base less readily. Strong acids have relatively weak conjugate bases (i.e. when the equilibrium of Equation (3·1) lies to the right), whereas weak acids have strong conjugate bases (equilibrium lying to the left).
The strength of an acid can be expressed as its dissociation constant, Ka, by applying the law of mass action* to the equilibrium of Equation (3·1). Thus the velocity of the reaction from left to right (V1) is given by the equation
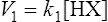 (3·2)
(3·2)where k1 is the velocity coefficient for the forward reaction and [HX] is the ‘activity’ of the acid HX which for dilute solutions, such as occur in living organisms, can to all intents and purposes be considered as equal to the concentration of the acid. Considering the reverse reaction, its velocity (V2) is given by
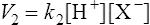 (3·3)
(3·3)where k2 is the velocity coefficient of the reaction from right to left and [H+] and [X−] are the concentrations of hydrogen ions and the conjugate base respectively.
When equilibrium is reached the velocities (V1 and V2) of the forward and reverse reactions are equal, so from Equations (3·2) and (3·3)
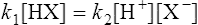
by cross multiplying we obtain the definition of the acid dissociation constant Ka:
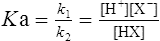 (3·4)
(3·4)In Table 3.2 a number of acids of biochemical interest are listed, together with their dissociation constants and conjugate bases. There is a considerable range of acid strengths, represented by the dissociation constants. These range from values greater than unity for the very strong mineral acids to very small values indeed, where Ka involves large negative powers of ten, e.g. for the third ionization of phosphoric acid and for water itself. Examination of the formulae in the first column of the table shows that acids may be either electrically neutral molecules, anions with one or more negative charges (e.g. the ion 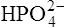 ), zwitterions (such as the zwitterionic form of glycine, NH3+ · CH2 · COO−) (page 41) and even cations (such as the ammonium ion
), zwitterions (such as the zwitterionic form of glycine, NH3+ · CH2 · COO−) (page 41) and even cations (such as the ammonium ion 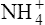 which is an acid because it has a tendency to lose a proton to form an electrically neutral ammonia molecule). Polybasic acids such as carbonic, citric and orthophosphoric acids have distinct values of Ka for each of their dissociable protons. These dissociation constants may lie close together as in citric acid, where they differ only by a power of ten, or spread far apart as in phosphoric acid, where the Ka values differ by factors of 105. The intermediate ions formed from polybasic acids can behave either as acids or bases according to their environment. Thus the dihydrogen phosphate ion
which is an acid because it has a tendency to lose a proton to form an electrically neutral ammonia molecule). Polybasic acids such as carbonic, citric and orthophosphoric acids have distinct values of Ka for each of their dissociable protons. These dissociation constants may lie close together as in citric acid, where they differ only by a power of ten, or spread far apart as in phosphoric acid, where the Ka values differ by factors of 105. The intermediate ions formed from polybasic acids can behave either as acids or bases according to their environment. Thus the dihydrogen phosphate ion 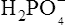 acts as an acid when it loses a proton to form the monohydrogen phosphate ion
acts as an acid when it loses a proton to form the monohydrogen phosphate ion 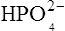 but as a base when it gains one to form orthophosphoric acid.
but as a base when it gains one to form orthophosphoric acid.
Table 3.2
Dissociation constants and pKa values at 25°C of some common acids of biochemical importance
| Formula of acid | Ka | pKa | Formula of conjugate base | |
| HCl | Hydrochloric acid | >2·9 | < −0·46 | Cl− |
| CH3·COOH | Acetic acid | 1·75 × 10−5 | 4·76 | CH3·COO− |
| CH3CH(OH)COOH | Lactic acid | 8·32 × 10−4 | 3·08 | CH3·CH(OH)COO− |
| C3H5O(COOH)3 | Citric acid | 9·20 × 10−4 | 3·04 | C3H5O(COOH)2COO− |
| C3H5O(COOH)2COO− | Citric acid | 2·69 × 10−5 | 4·57 | C3H5O(COOH)(COO−)2 |
| C3H5O(COOH)(COO−)2 | Citric acid | 1·34 × 10−6 | 5·87 | C3H5O(COO−)3 |
| H2CO3 | Carbonic acid | 4·31 × 10−7 | 6·37 | HCO3− |
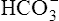 |
Carbonic acid | 5·61 × 10−11 | 10·25 | 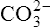 |
| H3PO4 |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


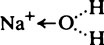 and the chloride ion as
and the chloride ion as 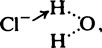 the arrow denoting donation of a free electron pair from the complete outer shell.
the arrow denoting donation of a free electron pair from the complete outer shell.