Introduction
The aim of this study was to determine the reliability and the measurement error (by means of the smallest detectable error) of 17 commonly used cephalometric measurements made on 3-dimensional (3D) cone-beam computed tomography images.
Methods
Twenty-five cone-beam computed tomography scans were randomly selected, and 3D images were rendered, segmented, and traced with the SimPlant Ortho Pro software (version 2.1, Materialise Dental, Leuven, Belgium). This was repeated twice by 2 observers during 2 sessions at least 1 week apart. Measurement error was determined by means of the smallest detectable difference. Differences were analyzed with Wilcoxon signed rank tests. Intraobserver and interobserver reliability values were calculated by means of intraclass correlation coefficients (ICC) based on absolute agreement.
Results
There were great variations of measurement errors between the angular (range, 0.88°-6.29°) and linear (range, 1.33-3.56 mm) variables. The greatest measuring error was associated with the dental measurements U1-FHPL, L1-MdPL. and L1-FHPL (range, 3.80°-6.29°). ANB angle was the only variable with a measuring error of 1° or less for both observers. The intraobserver agreement of all measurements was very good (ICC, 0.86-0.99). Except for SN-FHPL (ICC, 0.76), interobserver agreement was very good (ICC, >0.88).
Conclusions
The measurement errors of 3D cephalometric measurements (except for the ANB angle) can be considered clinically relevant. This questions the use of linear and angular 3D measurements to detect true treatment effects when a high level of accuracy is required.
Since the introduction of 3-dimensional (3D) cone-beam computed tomography (CBCT) for imaging the maxillofacial region a decade ago, the ability to show spatial relationships in all 3 planes has expanded the possibilities for diagnosis, craniofacial surgery planning, and outcome evaluation in orthodontics and oral maxillofacial surgery. The main advantage of CBCT technology is the significant reduction of radiation exposure compared with conventional computed tomography. With CBCT, it is possible to perform a full scan of the head in a few seconds with an effective dose of only 50 μSv compared with 2000 μSv from conventional computed tomography. Other advantages of CBCT are lower costs, increased accessibility to orthodontic practices, flexibility in the field of view, and submillimeter spatial resolution. The routine use of CBCT images in orthodontics and craniofacial surgery might not be far away.
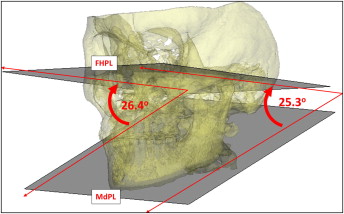
Due to their absolute accuracy, CBCT images have become powerful tools for evaluation of craniofacial morphology and treatment outcome. Accuracy is of utmost importance when the data from CBCT are used for presurgical planning to ensure correct jaw repositioning. However, accurate CBCT images or precise location of landmarks does not guarantee accurate measurements, since geometric factors can have a significant influence on 3D measurements. Moreover, each 3D landmark has its own unique configuration and envelope of error that contributes to measurement error. Recent studies have shown that the reliability of 3D landmark identification with CBCT is good and even more precise than conventional cephalograms when it is done by trained and experienced operators using the renderings and the cross-sectional slices in all 3 planes of space. In contrast to 2-dimensional (2D) cephalometry, with lines used for measurements, 3D measurements are often made to planes that might have a different orientation to each other from the frontal view. This means that the measurements between the planes might differ depending on the location of the measurement and can therefore be an additional source of error ( Fig 1 ).
Reliability of 3D measurements reported as correlation coefficients might have limited clinical value because good correlation does not imply a small measuring error. Unfortunately, only a few articles have reported the intraobserver and interobserver measurement errors associated with 3D measurements. However, it is difficult to draw conclusions from these articles because they used different methods and variables to describe 3D measurement errors. Nevertheless, the reported 3D measurement errors seem to be clinically relevant (>1 mm or 1°) considering the absolute level of accuracy required for surgical planning and outcome evaluation. Recently, we introduced the concept of the smallest detectable difference (SDD) in cephalometry to describe measurement errors. The SDD implies that, to be able to detect real change, the difference between 2 observations must be at least equal to or larger than the SDD for the specific measurement.
Since CBCT images are accurate, it is necessary to determine whether the numeric data of 3D cephalometric variables derived from the images are sufficiently accurate and reliable for surgical planning and outcome evaluation. The aim of this study was to determine the reliability and the measuring error by means of the SDD values of angular and linear measurements commonly used in 3D cephalometric analysis.
Material and methods
The sample consisted of 25 CBCT scans (from 13 male and 12 female patients) randomly selected at the Department of Orthodontics of the University Medical Center Groningen, University of Groningen, Groningen, The Netherlands. The average age of these subjects was 25.8 years (range, 11.7-49.5 years). Informed consent was obtained from the patients, and no identifying marks were used after selection of the CBCT scans. Patients with clefts and visible asymmetry (defined as a 4-mm deviation of menton from the midsagittal plane ) were not considered. The CBCT images were acquired with a 3D eXam scanner (KaVo Dental, Bismarckring, Germany) at a 0.30-voxel resolution. The CBCT data were exported from the eXamVisionQ software (Imaging Sciences International, Hatfield, Pa) in DICOM multifile format and imported into SimPlant Ortho Pro software (version 2.1, Materialise Dental, Leuven, Belgium) on an Aspirelaptop (7730G, Acer, s’Hertogenbosch, The Netherlands) with a dedicated 512 MB video card (Geforce 9600M-GT, NVIDIA, Santa Clara, Calif). The 3D surface models of all CBCT images were generated by means of a threshold-based method performed by 1 operator (J.D.). The surface model was saved, and the same surface model was used for each measuring session. All measurements were performed on a 17-in CrystalBrit LCD flat-panel color screen (Acer) with a maximum resolution of 1440 × 900 pixels. The SimPlant Ortho Pro software provides various views by rotation and translation of the rendered image. Before measurement, 2 experienced observers (with more than 3 years’ experience in 3D cephalometry; J.D. and Z.F.) discussed and reviewed the definitions of the anatomic landmarks ( Table I ) during a consensus meeting. The definitions of the landmarks and planes as defined by Swennen et al were used for this study. The 2 observers made the measurements separately. The same patient was measured at 2 times by each observer during 2 sessions at least 2 weeks apart. The anatomic landmarks were identified by using a cursor-driven pointer on the volume renderings and the cross-sectional slices in all 3 planes of the CBCT images. After landmark identification, a preprogrammed analysis provided the distances to the nearest .01 mm of the measurements described in Table II . The values were then exported and saved as Excel file format (Microsoft, Redmond, Wash).
| Landmark and abbreviation | Definition | |
|---|---|---|
| Unilateral landmarks | ||
| Sella | S | Sella is the center of the fossa hypophysialis |
| Nasion | N | Nasion is the midpoint of the frontonasal suture |
| Anterior nasal spine | ANS | The most anterior midpoint of the anterior nasal spine of the maxilla |
| A-point | A | A-point is the point of maximum concavity in the midline of the alveolar process of the maxilla |
| Upper incisor tip | Isi | Upper incisor tip is the middle point of the tip of the crown of the most prominent maxillary central incisor |
| Upper incisor apex | Isa | The middle point of the tip of the apex of the most prominent maxillary central incisor |
| Lower incisor incisal tip | Iii | Lower incisor tip is the middle point of the tip of the crown of the most prominent mandibular central incisor |
| Lower incisor apex | Iia | The middle point of the tip of the apex of the most prominent mandibular central incisor |
| B-point | B | B-point is the point of maximum concavity in the midline of the alveolar process of the mandible |
| Pogonion | Pog | Pogonion is the most anterior midpoint of the chin on the outline of the mandibular symphysis |
| Gnathion | Gn | Gnathion is the midpoint between Pog and Me on the outline of the mandibular symphysis |
| Menton | Me | Menton is the most inferior midpoint of the chin on the outline of the mandibular symphysis |
| Basion | Ba | Basion is the most anterior point of the foramen magnum |
| Bilateral landmarks ∗ | ||
| Gonion | Go | Gonion is the point at each mandibular angle that is defined by dropping a perpendicular from the intersection of the tangent lines to the posterior margin of the mandibular vertical ramus and the inferior margin of the mandibular body or the horizontal ramus |
| Condylion | Co | Condylion is the most posterior-superior point of each mandibular condyle in the sagittal plane |
| Orbitale | Or | Orbitale is the most inferior point of each infraorbital rim |
| Porion | Po | Porion is the most superior point of each external acoustic meatus |
| Posterior maxillary point | PMP | Posterior maxillary point is the point of maximum concavity of the posterior border of the palatine bone in the horizontal plane |
| Planes | ||
| Frankfort horizontal | FHPL | The Frankfort horizontal plane is defined by a plane that passes both Or left and Or right and the mean of the 2 porion (Po left and Po right) landmarks |
| Palatal | PPL | The palatal plane is defined by a plane that passes the ANS and both PMP left and PMP right |
| Mandibular | MdPL | The mandibular plane is defined by a plane that passes Me and both gonion (Go left and Go right) landmarks |
| Measurement | Description |
|---|---|
| Angular measurements (°) | |
| SNA | Angle between S and A with its vertex at N |
| SNB | Angle between S and B with its vertex at N |
| ANB | Angle between points A and B with its vertex at N |
| SN-FHPL | Angle between a line through S and N and the FHPL in the sagittal plane |
| SN-PPL | Angle between a line through S and N and the PPL in the sagittal plane |
| SN-MdPL | Angle between a line connecting S and N and the MdPL in the sagittal plane |
| PPL-MdPL | Angle between the PPL and the MdPL in the sagittal plane |
| y-axis | Angle between N and Gn with its vertex at S |
| U1-FHPL | Angle between a line through Isi and Isa and the FHPL in the sagittal plane |
| L1-MdPL | Angle between a line through Iii and Iia and the MdPL in the sagittal plane |
| L1-FHPL | Angle between a line through Iii and Iia and the FHPL in the sagittal plane |
| BaSN | Angle between N and Ba with its vertex at S |
| Linear measurements (mm) | |
| ANS-Me | Distance between ANS and Me |
| Co-A | Distance between the right Co and A-point |
| Co-Gn | Distance between the right Co and Gn |
| AFH | Distance between Me and N |
| PFH | Distance between S and the mean point between the left and right Go |
Statistical analysis
The standard error of measurement of the repeated measurements was calculated as the square root of the variance of the random error from a 2-way random-effects analysis of variance (ANOVA).The standard error of measurement was calculated for each angular and linear measurement. The SDD was then calculated with the formula: 1.96 × √2 × the standard error of measurement. The SDD was used to calculate intraobserver and interobserver measurement errors. As a measure of intraobserver and interobserver reliability, the intraclass correlation coefficient (ICC) for absolute agreement based on a 2-way random-effects ANOVA was calculated. Interobserver reliability was tested by comparing the first measuring sessions. Because not all variables were normally distributed (Shapiro-Wilks tests), nonparametric tests were used. Wilcoxon signed rank tests were used to compare the repeated measurements of each observer. In addition, Wilcoxon signed rank tests were used to compare the first measuring sessions by between the observers. P values less than 0.05 were considered significant. All statistical analyses were performed with a standard statistical software package (version 16, SPSS, Chicago, Ill).
Results
The results are reported in Table III . There were no significant statistical differences ( P <0.05) between the measuring sessions or the observers. The intraobserver reliability of the cephalometric measurements was very good (ICC, 0.86-0.99). The interobserver reliability of the 3D measurements was also very good. Except for PPL-MdPL (ICC, 0.76), the interobserver ICC values were all higher than 0.88. The measurement error (SDD) followed the same trends for both observers. The largest angular SDD values for both observers (3.80°-6.29°) were all dental measurements (U1-FHPL, L1-MdPL, and L1-FHPL). The smallest angular SDD for both observers was the ANB angle (0.88° and 0.98°, respectively). Only the ANB angle had an intraobserver measuring error of less than 1 mm, which is usually regarded as clinically relevant in cephalometry. The linear variable with the smallest SDD for observer 1 was Co-A (1.52 mm), and ANS-Me (1.33 mm) was the linear variable with the smallest SDD for observer 2. The interobserver measuring errors did not increase as expected; they were in the same range as the intraobserver measuring errors and followed the same trend as the intraobserver measuring errors.
| Intraobserver | Interobserver | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Observer 1 | Observer 2 | ||||||||||||||||
| T1 | T2 | Comparison (T1-T2) | T1 | T2 | Comparison (T1-T2) | Comparison (T1-T1) | |||||||||||
| Mean | SD (±) | Mean | SD (±) | ICC | P | SDD | Mean | SD (±) | Mean | SD (±) | ICC | P | SDD | ICC | P | SDD | |
| Angular measurements (°) | |||||||||||||||||
| SNA | 81.73 | 3.72 | 82.18 | 3.77 | 0.96 | 0.79 | 2.08 | 82.98 | 3.70 | 82.32 | 3.91 | 0.95 | 0.48 | 2.34 | 0.88 | 0.26 | 3.63 |
| SNB | 78.13 | 4.15 | 78.41 | 4.29 | 0.98 | 0.82 | 1.74 | 79.04 | 4.26 | 78.38 | 4.27 | 0.95 | 0.52 | 2.75 | 0.93 | 0.41 | 3.28 |
| ANB | 3.60 | 3.21 | 3.77 | 3.16 | 0.99 | 0.69 | 0.88 | 4.11 | 3.22 | 3.87 | 3.16 | 0.99 | 0.70 | 0.98 | 0.97 | 0.57 | 1.47 |
| SN-FHPL | 10.36 | 2.46 | 10.36 | 2.05 | 0.91 | 0.66 | 1.86 | 9.64 | 2.39 | 10.10 | 2.35 | 0.86 | 0.32 | 2.46 | 0.76 | 0.21 | 3.38 |
| SN-PPL | 7.20 | 3.37 | 6.73 | 3.52 | 0.90 | 0.68 | 3.06 | 6.65 | 3.61 | 6.94 | 3.67 | 0.92 | 0.95 | 2.91 | 0.86 | 0.67 | 3.60 |
| SN-MdPL | 31.59 | 8.07 | 31.70 | 8.19 | 0.98 | 0.95 | 3.39 | 31.17 | 8.32 | 31.85 | 8.44 | 0.98 | 0.87 | 3.31 | 0.97 | 0.80 | 3.64 |
| PPL-MdPL | 24.46 | 7.92 | 25.04 | 8.02 | 0.98 | 0.82 | 3.25 | 24.73 | 7.94 | 25.02 | 8.17 | 0.97 | 0.85 | 3.66 | 0.98 | 0.93 | 2.77 |
| y-axis | 67.59 | 4.91 | 67.54 | 4.87 | 0.98 | 0.99 | 2.11 | 67.29 | 5.14 | 67.97 | 4.98 | 0.95 | 0.50 | 2.87 | 0.96 | 0.71 | 2.96 |
| U1-FHPL | 67.32 | 8.69 | 66.35 | 8.47 | 0.96 | 0.68 | 4.81 | 66.38 | 9.27 | 67.22 | 8.32 | 0.98 | 0.63 | 3.80 | 0.97 | 0.55 | 4.57 |
| L1-MdPL | 80.44 | 6.47 | 80.21 | 6.95 | 0.89 | 0.93 | 6.29 | 80.73 | 6.57 | 81.21 | 6.30 | 0.93 | 0.76 | 5.77 | 0.89 | 0.91 | 6.11 |
| L1-FHPL | 63.63 | 8.10 | 64.21 | 8.25 | 0.95 | 0.82 | 4.93 | 64.05 | 7.90 | 64.11 | 7.48 | 0.96 | 0.89 | 4.46 | 0.96 | 0.85 | 4.56 |
| BaSN | 132.21 | 5.60 | 131.97 | 5.74 | 0.96 | 0.82 | 3.17 | 131.75 | 5.95 | 132.53 | 5.46 | 0.96 | 0.46 | 3.27 | 0.93 | 0.63 | 4.22 |
| Linear measurements (mm) | |||||||||||||||||
| ANS-Me | 66.95 | 8.66 | 67.38 | 8.67 | 0.99 | 0.82 | 2.00 | 67.34 | 8.68 | 67.06 | 8.79 | 0.99 | 0.86 | 1.33 | 0.99 | 0.84 | 2.12 |
| Co-A | 96.08 | 5.62 | 95.87 | 5.75 | 0.99 | 0.88 | 1.52 | 95.87 | 5.76 | 95.69 | 5.49 | 0.98 | 0.95 | 2.33 | 0.99 | 0.79 | 1.42 |
| Co-Gn | 122.21 | 8.13 | 122.08 | 8.34 | 0.99 | 0.98 | 1.80 | 121.97 | 8.36 | 122.58 | 8.34 | 0.99 | 0.74 | 2.85 | 0.99 | 0.90 | 2.20 |
| AFH | 116.72 | 10.66 | 116.73 | 10.85 | 0.99 | 0.97 | 1.89 | 116.59 | 10.99 | 116.85 | 11.04 | 0.99 | 0.90 | 2.13 | 0.99 | 0.96 | 2.68 |
| PFH | 75.78 | 6.51 | 75.88 | 6.02 | 0.97 | 0.94 | 2.79 | 76.21 | 6.30 | 76.00 | 6.37 | 0.96 | 0.85 | 3.56 | 0.96 | 0.66 | 3.60 |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


