Introduction
The aim of this study was to propose a method to classify dental arch forms of subjects with normal occlusion into several types that can ensure both goodness of fit and clinical application.
Methods
We selected 306 subjects with normal occlusion from 15,836 young adults, recorded 14 reference points that defined the distance between 2 arch forms as the area between 2 arches, and then classified the dental arch forms by using the partitioning around medoids clustering and silhouette method. We measured tooth size, arch width, basal arch width, arch depth, mesiodistal angulations, and buccolingual inclinations.
Results
We identified 3 types of arch forms, and cross-classification of the maxillary by mandibular arch forms showed a more frequent distribution in the diagonal elements than in the off-diagonal elements. The 3 arch forms showed differences in tooth size, arch width, basal arch width, and inclination of the posterior teeth.
Conclusions
By defining area discrepancies as distance measures and applying them to the cluster method by using medoids, the dental arch form can be classified keeping control for the extremes without bias. It is hoped that this method will have possible clinical applications in determining the shape and number of preformed orthodontic arch forms.
The development of the preadjusted bracket allowed orthodontists to concentrate more on diagnosis, treatment planning, and treatment mechanics rather than on complicated archwire bending. However, with preadjusted brackets, selection of a preformed archwire has become a more important step in clinical orthodontic practice that is often overlooked.
As evidenced by the many types of arch forms available, orthodontists do not agree on a single arch-form shape. Previous studies have mainly focused on describing and fitting arch forms geometrically or mathematically in a more accurate manner. Many authors claimed that there might be a standard form of dental arch and some geometric or mathematical curve; eg, semicircle ; ellipse ; parabola, hyperbola ; catenary curve ; cubic spline function ; conic sections ; polynomial functions including second-order polynomial, fourth-order polynomial, sixth-order polynomial ; Euclidean distance matrices ; Fourier series ; beta function ; and Bezier cubic equation were once described as standard ideal forms that should fit the dental arch and ensure accuracy in describing arch forms. Today, however, many normal variations are emphasized more than the specific type of arch forms. Recent studies nullify the existence of a single ideal arch-form template, indicating that dental arch forms are highly individual, and defining a single generalized shape and using variations of it should be avoided. Once the arch form has been described with a certain geometric or mathematical function, the problem of how to define or classify the dental arch into several types systematically without observer bias still remains.
Arch-form classification is especially important when using shape-memory wires. Although there are commercial forms, the forms are classified not by scientific basis but merely by beliefs of some orthodontists concerning arch forms. Some previous investigators used commercial arch forms for their arch-form related research: eg, OrthoForm (3M Unitek, Monrovia, Calif), Pentamorphic arch template (Rocky Mountain Orthodontics, Denver, Colo), Tru-Arch (Ormco, Sybron Dental Specialties, Orange, Calif), and Brader (American Orthodontics, Sheboygan, Wis) among others. However, there is a certain degree of subjectivity in the classification of dental arch forms. The form is not based on any data but, rather, is predicated on the clinical experiences or preferred forms of certain clinicians or companies. Furthermore, the studies of Felton et al and Camporesi et al showed neither a predominance of any particular arch form among commercially available arch forms, nor a superior closeness of fit.
We postulated that the classifications and clinical applications are inversely related to each other. Thus, if a classification is not accurate, there will be no accuracy in fit. Inversely, if classification becomes too prescriptive, it interferes with the practical use—clinicians’ selection, inventory management, and so forth. Therefore, cluster analysis helps to determine the number of classifications so that the best fit can be achieved with maximum between-group distances. Originally, cluster analysis was used to identify certain groups of observations that are cohesive and separated from other groups. Multivariate cluster analysis is a relatively new method in biomedical science and can interpret an entire set of data while preserving information about individuals. In dentistry, a possible application of this methodology could be to classify dental arch forms without practitioner bias.
The aim of this study was to develop a method to classify dental arch forms that are difficult to identify from subjective visual inspection into several forms that can ensure both goodness of fit and pragmatic clinical application.
Material and methods
A total of 306 subjects with normal occlusion were selected from 15,836 young Korean adults who responded to a community dental health survey from 1997 to 2005 in Seoul, Korea. They included 187 men and 119 women with a mean age of 20.0 years (range, 17-24 years). The selection criteria were (1) Class I molar and canine relationships with normal occlusal interdigitation, (2) complete permanent dentition erupted except the third molars, (3) normal overjet and overbite (about 2-4 mm), (4) minimal crowding (<2 mm) and spacing (<1 mm), and (5) no previous orthodontic or prosthodontic treatment. In addition, subjects with proximal caries or fillings that affected a tooth’s size and shape, gross restorations, significant attrition, congenital defects, or deformed teeth were excluded. Absence of tooth anomalies of structure and development was also considered. The subjects were part of the Korean Standard Occlusion Study, which has been ongoing since 1997.
Dental stone casts were made from alginate impressions, and the sizes of the teeth were measured by using digital Vernier calipers (Mitutoyo; Kawasaki, Kanakawa, Japan) with sharpened points under an illuminated magnifier (Otsuka Optics, Tokyo, Japan) from the central incisors to the second molars (accurate to 0.01 mm). The size of each tooth was defined as the mesiodistal width measured from its mesial contact point to its distal contact point of its greatest distance, as suggested by Jensen et al.
Arch width, basal arch width, and arch depth were measured from the canines up to the second molars. A centroid was constructed for each cusp tip, which was relatively independent of cusp wear or abrasion. The definition of basal arch width referred to the distance between the apical third of the alveolus as suggested by Howes.
In addition, several proportional variables were measured, including arch width-arch depth, intercanine-intermolar width, anterior curvature (sum of the anterior tooth sizes and intercanine width), and arch width ratio (maxillary arch width to mandibular arch width as a percentage).
An angulation-and-inclination measuring gauge (Invisitech, Seoul, Korea) was used to record angulation and inclination of a tooth on a dental cast. A level and a dental surveyor kit with a laboratory jack were used to ensure the flatness of the measuring field, and the dental cast was positioned parallel to the functional occlusal plane as described by Lee et al, Kim et al, and Lee et al. The 3 pointers on the measuring gauge were directed toward the facial axis of the clinical crown with the middle pointer aimed toward the facial axis point as described by Andrews.
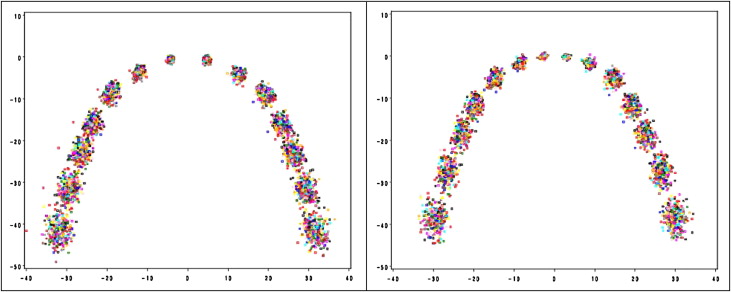
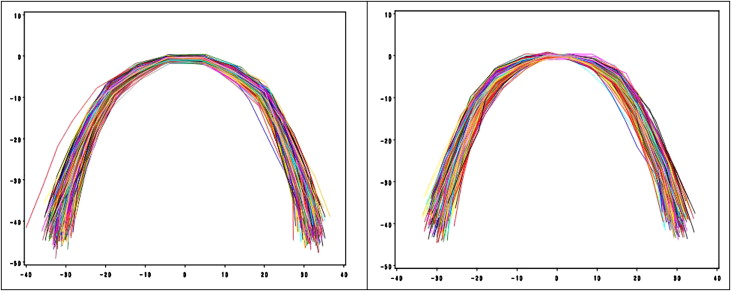
Dental casts were photocopied, the 14 reference points from the central incisors to the second molars were digitized (Intuos 2 Graphic Tablet; Wacom, Toyonodai, Kazo-shi, Saitama, Japan) and converted into Cartesian coordinates with custom-made software in Delphi (CodeGear, Scotts Valley, Calif) programming language ( Fig 1 ). The set of data points in Figure 1 was chosen to represent the dental arch forms of the maxilla and the mandible. The problem was that the reference points are neither on a smooth curve nor symmetric. To overcome the problem, we interpolated the data points of each subject using the piece-wise linear function for further cluster analysis ( Fig 2 ). The observed data points were not registered well because superimpositions of the observed arches were inconsistent in the origin and therefore randomly rotated left or right. To resolve this difficulty, we defined a new distance between 2 arch forms that is invariant to location shift and rotation transformation.
Suppose (x,f(x))
( x , f ( x ) )
and (x,g(x))
( x , g ( x ) )
are 2 continuous functions representing 2 arch forms. The new distance d{(x,f(x)),(x,g(x))}
d { ( x , f ( x ) ) , ( x , g ( x ) ) }
, simply denoted by d(f,g)
d ( f , g )
, is defined as:
d ( f , g ) = inf T [ δ , ] ∈ T Ω ∫ | f ( x ) − T [ δ , ] g ( x ) | d x ,
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


