Criticisms of previous reports evaluating angular or linear measurements and the limitation of the Bland-Altman plot for 2D cephalometric data

Traditionally, in studies with cephalometrics, errors of measurement are considered to arise from both the actual identification of the landmarks and the linear or angular measurements derived from those landmarks. Since cephalometrics has not been an exact science, we orthodontists recognize that certain latitude must be granted to a person tracing cephalometric radiographs and that errors are likely to occur. Traditionally in cephalometrics, landmark identification errors or prediction errors have been most commonly reported with 1-dimensional variables, such as linear or angular measurements: ie, linear measurements between 2 landmarks separately in either the horizontal (x-axis) or the vertical (y-axis), or degrees of angles among 3 points.

The problems associated with the reliability of linear and angular measurements are that a linear measurement is formed from 2 points and an angle is formed from 3 points. Measuring errors by using linear and angular measurements cannot pinpoint the error from the related points. In general, a distance measurement is more precise or reliable than an angular measurement. For example, when reporting the reliability of a measured angle, such as ANB (SNA–SNB), the source of error could be partly due to the unreliability of locating any of the 3 related points (nasion, Point A, and Point B), and the variation among the location of the points can also be compounded when determining the measured angle. In some situations, the points themselves might not be significantly different but, when added together, produce a different angle.

With regard to the 1-dimensional graphic visualization of the error report, Bland and Altman developed a simple, intuitive, and easy method to show a reliability measure between 2 variables. Their simple descriptive analysis permits the assessment of the agreement between 2 imperfect clinical measurements or the repeatability of duplicate observations. As long as there is only 1 variable, the Bland-Altman plot can be used to evaluate both intraobserver and interobserver reliabilities. This method has become increasingly popular in orthodontic publications. Nonetheless, when a variable has a 2D entity, the Bland-Altman plot cannot visualize both x-axis and y-axis errors simultaneously in the 2D plane.

Reliability reports for 2D data in the 2D plane

In this section, we use a real clinical example for illustration. These data are from a clinical study by Suh et al ; it suggested the appropriateness of a new method (method 2) over the conventional least-squares method (method 1) to predict soft-tissue changes after orthognathic surgery. The subjects included patients (n = 69) who had undergone surgical correction of Class III mandibular prognathism by only mandibular setback surgery. In this example, we selected 2 simple but important cephalometric landmarks—soft-tissue pogonion and soft-tissue menton—from among the variables in the original study. After applying the conventional least-squares prediction method to the test data set (also called the validation data set), the result of the prediction errors (or the systematic error, also called bias) did not show a significant difference in either the x-axis or the y-axis. However, since overestimations and underestimations of the predictions essentially cancel themselves out when mean values are derived, a comparison test using the mean values in a reliability report is not appropriate. A graphic representation is again the best method.

In a 2D situation, a scattergram can be plotted in 2D space. In a scattergram, a negative value indicates that the prediction is more posterior in the x-axis or more superior in the y-axis compared with the actual result ( Fig ). If, and only if, errors in both the x-axis and the y-axis were normally distributed (Gaussian) and the x-axis and the y-axis did not show a linear association between them (no correlation) and the 2 errors have the same variance, the plots would form a perfect circle. Usually, this can be seen by standardization: ie, subtracting means from individual values and then dividing by their standard deviations. In most cases, the plots form an ellipse with some deformation. After plotting the errors, ellipses can be depicted ( Fig ). The ellipsoid satisfies ( z – μ ) ^T Σ ⁻¹ ( z – μ ) ≤ χ ² (α) ₂ , where z is the 2D (x and y coordinates) vector for the error, μ is the mean vector for z , Σ ⁻¹ is the inverse matrix of the covariance matrix, and χ ² (α) ₂ is the upper 95th percentile of a chi-square distribution with 2 degrees of freedom.

Scattergrams and 95% confidence ellipses for the errors that were obtained from conventional method 1 ( red ) and alternative method 2 ( blue ). The plots clearly indicate that the errors in both the x-axis and the y-axis were greater in method 1 than in method 2. This implies that the application of the method to a subject might give rise to errors to this extent with 95% probability.

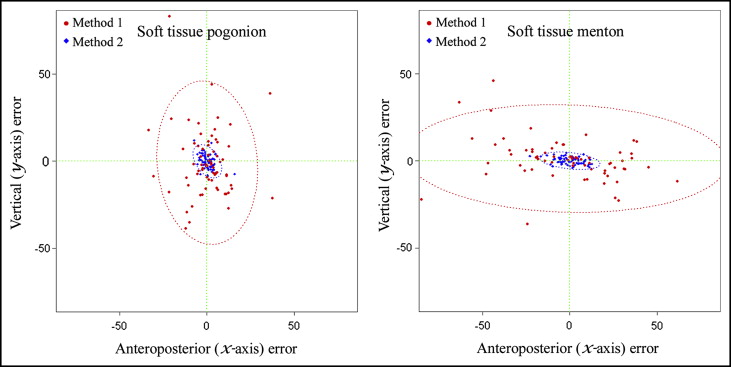
A scattergram with an ellipse representing plot points is essentially a 2D extension of the Bland-Altman plot. A Bland-Altman plot has 2 horizontal lines, the lower and upper agreement limits; they indicate which plotted data points are within the mean difference ± 2 SD. The range between the lower and upper limits also indicates the so-called 95% limits of agreement. Likewise, the contour of an ellipse in a scattergram also indicates the 95% confidence boundary. If any points are outside the 95% confidence boundary of the ellipse on the graph, they can be called outliers, just like plot points that are outside the horizontal lines of the Bland-Altman plot graph.

There are several advantages when using a 2D scattergram and a 95% confidence ellipse.

• 1.

  It can visualize not only the reliability but also the result of method comparisons. This can be done easily by assigning a different type or different color of dots for the second observer, or for the repeated measurements of an alternative method being compared. The mode of comparison can be expanded to more than 2 groups by changing colors and point characters. In the Figure, for example, we assigned red circles and blue diamonds, respectively, for methods 1 and 2. After comparing the sizes of the 95% confidence ellipses, we see that method 1 gives significantly larger ellipses than does method 2. Therefore, as shown by the graphs in this example, it is immediately obvious that method 2 has a significantly more accurate and higher predictive performance than does method 1.

• 2.

  The form and shape of the ellipse imply the correlation between the x-axis and the y-axis errors. A perfect circle indicates perfect independence and normality between the x-axis and the y-axis errors of a variable. A more deformed ellipsoid indicates greater correlation between the x-axis and the y-axis values.

• 3.

  The scattergram and the 95% confidence ellipse can leave something to interpret. For example, the soft-tissue pogonion graph ( Fig , left ) shows more errors in the vertical axis than in the horizontal axis. On the other hand, errors in the soft-tissue menton graph ( Fig , right ) are distributed more horizontally than in the vertical direction. This might partly be related to the definition of the cephalometric landmarks themselves, pogonion and menton. For example, when locating the most anterior point of the chin, pogonion, it is probably easier to determine the position on the x-axis coordinate than on the y-axis, thus producing the large vertical variation in the distributions for pogonion. By the same token, since menton is the most inferior point of the chin, there is greater horizontal variation in the x-axis than in the y-axis. Without graphic visualization, this interpretation would have been difficult.

In this article, the language R program (Vienna, Austria) was used. R is a free software for statistical computing. Detailed codes of the example data sets and plots for use with language R are available by request to the authors. Recently, more studies involving 3D imaging technology have been published. We envision that an easy 3D statistical graphic presentation for 3D data reliability will also be introduced soon.