Introduction
Young’s modulus (E) and Poisson’s ratio (v) of the periodontal ligament are needed in a finite element analysis for investigating the biomechanical behavior of a tooth, periodontal ligament, and bone complex. However, large discrepancies in E (0.01-1,750 MPa) and v (0.28-0.49) were reported previously. The objective of this study was to narrow the ranges and to provide equivalent E and v pairs suitable for finite element modeling of a tooth, periodontal ligament, and bone complex by using a reported crown load-displacement relationship as the criterion.
Methods
A 3-dimensional finite element model of a 3-tooth, periodontal ligament, and bone complex, consisting of a maxillary central incisor with 2 adjacent teeth, from a cone-beam computed tomography scan was created. The dimensions, constraints, and loading condition were kept similar to those reported in the human study. With the load applied to the crown, both v and E were adjusted independently, and the corresponding crown displacements were calculated. The resulting load-displacement curves were compared with those reported in the human study. The mean absolute displacement difference method was used to find the best fit. The E and v pairs that generated the minimum mean absolute displacement difference were identified.
Results
The finite element model with 1 of the 3 E and v pairs (v = 0.35, E = 0.87 MPa; v = 0.4, E = 0.71 MPa; and v = 0.45, E = 0.47 MPa) simulated the tooth, periodontal ligament, and bone complex well. The mean absolute displacement differences were 0.0135, 0.0138, and 0.0138 mm, respectively; these are less than 8% of 0.175 mm, which was the crown displacement of the tooth, periodontal ligament, and bone complex under the load of 500 cN.
Conclusions
The E and v values close to the 3 pairs might be used for finite element modeling of the tooth, periodontal ligament, and bone complex.
The finite element method is widely used to investigate biomechanical behaviors of tooth, periodontal ligament (PDL), and bone complex. In a finite element analysis, 2 mechanical parameters of the PDL are needed: Young’s modulus (E) and Poisson’s ratio (v). These parameters are critical in model accuracy because they primarily determine the deformation of the PDL, which directly links to the calculated stress and strain as well as the instantaneous crown displacement in response to orthodontic forces.
Previous studies have reported quite different values of E and v. Especially, E values were reported in a large range, from 0.01 to 1,750 MPa. Pietrzak et al determined the values of E as from 0.01 to 0.03 MPa by correlating the result of a nonlinear elastic finite element model to experimental data of a maxillary incisor under axial loadings. Siebers and Poppe et al used a bilinear parameter set for the elasticity of the PDL and determined the set values of E as approximately 0.05 and 0.28 MPa. Anderson et al determined the value of E as 0.07 MPa using a linear-elastic finite element model. Yoshida et al determined the values of E from 0.12 to 0.96 MPa for different load ranges and claimed that E increased almost exponentially with the increment of load because of the PDL’s nonlinear elasticity. Jones et al stated that an appropriate estimate of E was 1 MPa, through direct measurement on human subjects. Yamada and Evans, Mandell et al, and Atkinson and Ralph determined the values of E as 1.4, 2.4, and 3.0 MPa, respectively. Rees and Jacobsen determined the value of E as 50 MPa by correlating the result of a 2-dimensional plain strain finite element model with 2 experimental loading studies. Atmaram and Mohammed determined the value of E as between 175 and 350 MPa using 2 types of PDL elements in a finite element model. Most previous finite element studies used E values in the ranges in these reports. The primary reason for the wide discrepancies lies in the difficulties of investigating the physical PDL parameters. First, the parameters are determined by the internal physical and biologic properties of the PDL, and intensive and thorough knowledge of the PDL is limited. Second, there is no benchmark approach to investigate these parameters in the PDL; this makes it difficult to judge the validity of the reported data.
Considering the great needs of finite element analysis and the importance of the 2 parameters, E and v, in the analysis, the objectives of our study were to narrow the ranges of E and v, and to provide E and v pairs suitable for more reliable finite element modeling of the tooth, PDL, and bone complex. We were not intending to investigate the physical parameters of the PDL, but rather to find the best equivalent E and v pairs.
Material and methods
The objectives were achieved by simulating an in-vivo study by using the finite element method. This study included creating a comparable tooth, PDL, and bone complex finite element model with the same loading conditions as reported in the in-vivo study, adjusting the E and v individually and calculating the resulting displacements, and selecting the E and v pairs from the crown displacement that agreed with the in-vivo experimental result. These were considered as the equivalent E and v pairs.
Christiansen and Burstone quantified the crown displacements in response to applied forces on the maxillary central incisors in vivo. In this study, the force was applied to an extension bar at Point B ( Fig 1 ). The bar was along the long axis of the measured tooth and attached to the crown. Displacements of 2 other points, A and C, on the extension bar were measured simultaneously ( Fig 1 ). These points were measured for calculating both tooth translation and rotation. Based on the geometric relationship, the displacement of Point, B, where the force was applied, was calculated. Thus, an experimental load-displacement relationship was obtained. The relationship was primarily determined by E and v; thus, it was used as the criterion to determine the equivalent E and v for finite element modeling.
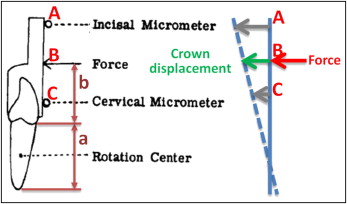
Cone-beam computed tomography images of a selected maxillary central incisor with the 2 neighboring teeth were used to create a finite element model that was comparable with the in-vivo case. The 3-dimensional roots and bone were reconstructed by using Mimics software (version 13.0; Materialise, Leuven, Belgium). The roots were segmented first. The PDL was created surrounding the roots by dilating the roots with 1 voxel (0.25 mm). The teeth, PDL, and bone were assembled to create a virtual tooth, PDL, and bone complex called the solid model. The solid model was then imported into software (version 12.1; ANSYS, Canonsburg, Pa) for meshing and analysis. Geometric parameters affecting the crown displacement in response to the force were kept the same as those in the in-vivo study. The key parameters included the distance, a , from the apex to the alveolar crest (16.8 mm) and the location, B , on the extension bar that is 14.8 mm above the alveolar crest to apply the horizontal force ( Fig 2 ). The study was approved by the Indiana University review board.
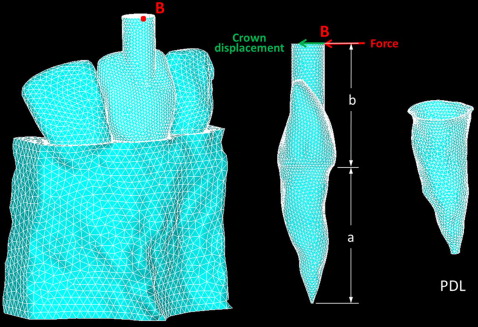
The tooth, PDL, and bone complex was considered homogeneous and isotropic. The material properties of the bone and the tooth were chosen from the literature ( Table ). The teeth, PDL, and bone were meshed with 10-node tetrahedral (SOLID187) elements. The numbers of elements of the target teeth, PDL, and bone were 82,020, 9907, and 84,507, respectively. The side surfaces of the 3-tooth model were fixed. Different static forces ranging from 0 to 500 cN were applied at B, which was perpendicular to the tooth’s long axis as was done in the in-vivo study. The resulting crown displacements at Point B were calculated.
| Tissue | Model characteristic | Young’s modulus | Poisson’s ratio |
|---|---|---|---|
| Tooth | Linear elastic | 2 × 10 10 Pa | 0.3 |
| Bone | Linear elastic | 3.45 × 10 8 Pa | 0.3 |
| PDL | Linear elastic | – | – |
The equivalent E and v pairs were determined in 2 steps. First, the E range was narrowed, based on the displacement from a 300-cN force from the in-vivo study. Then, the E in the newly determined range was fine-tuned based on the entire experimental load-displacement relationship. Compared with the E value, v has a narrower range, 0.28-0.49, as reported previously. Commonly, v values of 0.35 and 0.45 were used for the fibrous and nonfibrous matrix of the PDL, respectively. Therefore, 3 representative values of v = 0.35, 0.4, and 0.45 were selected first. Considering the values of E used in previous studies, E values in the range of 0.1 to 1,000 MPa were considered. For each selected v, E was adjusted to 0.1, 0.25, 0.5, 1, 2.5, 5, 10, 100, and 1000 MPa, respectively. A 300-cN force was applied, and the resulting displacement of Point B was calculated. The E and v pairs that resulted in the displacement closest to the in-vivo one were selected; this resulted in a narrowed range. Next, E in the new range paired with a v was used, and the crown displacements, resulting from orthodontic forces between 0 and 500 cN at a 100-cN increment, were calculated by using the finite element model. The load-displacement relationships were then compared with the experimental load-displacement relationship reported for determining the best fits. The equivalent E and v pairs should be the best fits of the entire load-displacement curve. For this purpose, the mean absolute displacement difference method was used to determine the best fits. The mean absolute displacement difference is a measure of statistical dispersion by using the average absolute difference, which is widely used for curve fitting. Regarding this study, the mean absolute displacement difference considered the differences between crown displacements simulated in the finite element model and these reported in the in-vivo study, under the forces from 0 to 500 cN. For each E and v pair, the mean absolute displacement difference was calculated as
MADD = | D 0 − D 0 ‘ | + | D 1 − D 1 ‘ | + | D 2 − D 2 ‘ | + | D 3 − D 3 ‘ | + | D 4 − D 4 ‘ | + | D 5 − D 5 ‘ | 6
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


