Introduction
The aim of this study was to investigate a new digital 3-dimensional infrared video system to determine its accuracy, precision, and validity in measuring facial distances.
Methods
Bench experiments were performed by measuring the vertical and diagonal distances of chessboard squares of known length to determine the system’s accuracy and precision. To test the system’s validity, 16 healthy volunteers participated in this study. Vertical and horizontal distances of the face were measured electronically at rest, and on posed and aggressive smiles. All measurements were repeated after 8 weeks. Direct measurements of the intercanthal distance were obtained twice with calipers.
Results
A minor systematic error was found in the bench experiments, with the highest absolute error of 0.227 ± 0.39 mm. The analysis with this video system showed good reproducibility of all measured distances when the mean of 2 frames was used to compare distances. Digital measurements of the intercanthal distances showed high agreement with the clinically obtained values.
Conclusions
This digital video system can measure geometric distances in a 3-dimensional environment with high precision. Facial distances can be measured with good accuracy and precision, allowing applications in research and clinical practice.
The development of facial average values, sex and facial growth analyses, and the examination of craniofacial anomalies are some examples of static assessments used in many fields of dental and medical research. It is common, for example, to see these applications used in orthodontics and orthognathic surgery to evaluate and compare treatment outcomes. In addition to these static assessments, dynamic analyses are often used to evaluate craniofacial syndromes, face size and shape, sex, and ethnic origin. The benefit of dynamic analyses comprises the ability to describe objectively the functions of the facial muscles and to evaluate impairment. The objective assessment of facial features and facial mobility in orthodontics allows evaluating some aspects of craniofacial diseases and treatment outcomes. The characterization of the mimic muscles can be useful for patients with facial motor deficits such as cleft lip and palate. Discrepancies in the dentofacial region are a major underlying factor influencing the mimic musculature. Orthodontic and orthognathic surgical treatment can influence significantly the cranial hard-tissue structures and lead to adaptions of the facial musculature.
The study of orofacial functions is also important in psychological and psychosocial studies. Deficits in the ability to communicate emotions by facial expressions might also play an important role in the clinical manifestation of schizophrenia and several other neuropsychiatric disorders. Another application of the study of orofacial function is in pain detection. For example, in demented patients, pain detection might be facilitated by mimic expression analyses. Thus, applications in psychiatry and geronto-psychiatry also seem plausible.
Traditional assessment of facial movement and mimic dysfunction in neurology and otolaryngology is performed by a trained observer using a descriptive grading system, most commonly the House-Brackmann grading system. It is based on a 6-grade scale that relies on subjective evaluations. The easy and straightforward use of this descriptive system explains its widespread clinical application. However, its lack of interrater agreement has often been criticized.
Until recently, researchers analyzed patient photographs in 2 dimensions or by interposition of 2 photographs in 3 dimensions (2D and 3D photogrammetry). Calipers were also used to assess the face in rest and function. Frey et al stated in 1994 that only 3D analysis could adequately assess complex facial movements. Efforts to visualize, measure, and objectively assess facial asymmetry or dyskinesia were supported by the rapid development of computer-aided photo and video analyses over the last 15 years. Several computer-based video systems were developed and validated to track the movements of the facial soft tissues.
One successful early measurement systems was described by Frey et al. The Vicon system was used to measure distances between markers attached to facial landmarks. The system allowed free facial movements and had a system-dependent error of the measurements of less than 1 mm.
Weeden et al evaluated the video-based tracking system “Motion Analysis” on healthy subjects and patients. The system also requires reflective markers to be attached to the landmarks. Using this 3D camera system they were able to detect differences of facial movement between the impaired patients and the controls, and to demonstrate an influence of sex and facial shape on border facial movements.
Tzou et al demonstrated ethnic differences in dynamic facial movements between healthy European and Asian cohorts using a camera system, a mirror setup, and customized software. Thus, the landmark displacements were evaluated in 3D. The system also required markers attached to facial landmarks.
Linstrom used the peak motus motion measurement system to detect and quantify facial synkinesis and paralysis, but the system did not allow free movement of the mimic muscles, because a chin support was needed to stabilize the head. At the same time, an objective grading system based on relative asymmetry of movement was proposed. Hontanilla and Auba developed a system that could track reflective dots on the human face and calculate distances. Mehta et al validated the 3-D geometry video acquisition system (3-D VAS) for facial motion analysis as a useful and accurate tool without marking landmarks.
The purpose of this study was to evaluate a new digital 3D infrared (IR)-based video system for research and clinical application. The following hypotheses were tested: the system measures geometric distances under bench and clinical conditions with high accuracy (veracity) and precision (reproducibility), and opto-electronically obtained intercanthal distances correspond to the values obtained with calipers under clinical conditions (validity).
Material and methods
Sixteen healthy volunteers, 8 women and 8 men (average age, 30.5 ± 3.6 years; range, 24-37 years), participated in this study. They were recruited from dental students and staff of the dental school of Geneva University in Switzerland. Approval from the ethics committee of the Geneva University Hospital was obtained in the context of a larger study.
The study was conducted with the SmartEye Pro-Mimic Muscle Evaluator (MME) system, which is based on SmartEye Pro (version 3.7, SmartEye AB, Gothenburg, Sweden). The SmartEye system was originally developed for gaze tracking and is used in the automotive industry for detecting driver fatigue. It is also designed to trace mimic movement such as eyelid closure.
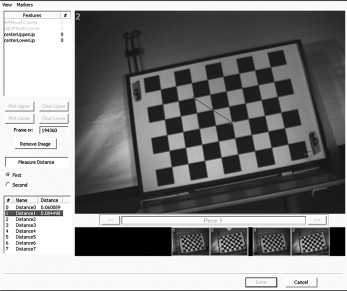
The hardware consisted of a standard personal computer (Dell Cooler Master [Dell, Round Rock, Tex]; Intel core, 2 CPU, 1.86 GHz, 1GB RAM, ASUS extreme AX550 graphic card [Intel, Santa Clara, Calif]; Windows XP home edition SP2 [Microsoft, Redmond, Wash]), 2 IR cameras with mounted IR emitters and an external processor. The latter had connectors for each camera, and the IR flashes were directly connected to the cameras (system works only with IR light with a wavelength of 845-850 nm). The system works with 2 to 5 cameras that can be positioned freely; subsequent calibration is necessary. In this study, the system comprised a 2-camera setup set to run at a sampling rate of 60 Hz. The resolution of the cameras was 640 × 480 pixels. They were mounted on aluminum bases that were adjustable in all axes ( Fig 1 ).

For calibration purposes, the system comes with a black-and-white chessboard with a size of 340 × 240 mm. The board has a foamed plastic core and smooth plastic layering. The side length of 1 square is 30 mm.
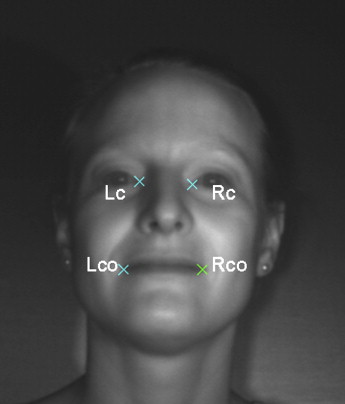
After the semi-automatic creation of a head profile, the SmartEye software calculates a 3D head model based on defined facial features such as the inner and outer corners of the eye, inner eyebrow, earlobes, mouth corners, and nostrils.
Custom-made SmartEye MME software extends the existing features by allowing tracking of additional landmarks and calculating distances, lines, and angles between them in a continuous video stream. Therefore, the position of each marked point in the corresponding images is calculated by its position on the x-, y-, and z-axes (output of these data is provided in the MME software). The automatic tracking feature of facial landmarks was unreliable in preliminary analyses, probably because of a lack of contrast in the videos. Therefore, distances were measured manually in each video frame (mouth dialogue). For each frame, the system provides 2 images in which corresponding landmarks are tagged ( Fig 2 ). Defining 1 landmark in 1 video freeze image requires marking it once in the image from the first camera and once in the image from the second camera. The system then calculates the distances between these landmarks in a 3D environment. The system has a precision of 0.001 mm. The values obtained were rounded to 0.01 mm for the bench experiments, and to 0.1 mm for the clinical experiments. This precision is frequently used in reference publications. It also considers the spatial capacity of the human eye, which is about 0.3 mm at a distance of 0.5 m.
Measurements on each participant’s face were made with a digital caliper (FINO Schieblehre digital, DT&SHOP, Bad Bocklet, Germany).
Each measurement with the Smart-Eye system was preceded by a calibration procedure by using the chessboard, which was hand held in front of the cameras. Small movements in the frontal plane facilitated its detection by the software.
In the first series of video sequences, the static chessboard was recorded. Initially, it was mounted upright in front of the cameras. The length of 2 squares (60 mm) and the diagonal over 2 squares were measured. Three measurements from different frames of the video recording were taken for each of the following positions of the chessboard ( Fig 2 ): (1) distance of 1.00 m with the chessboard upright in front of the cameras, (2) distance of 1.00 m with the chessboard inclined forward by 15° in the y-axis (position 2), (3) distance of 1.00 m with the chessboard tilted to the right by 15° in the z-axis (position 3), and (4) positions 2 and 3 combined.
The measurements were repeated with distances of 1.05 and 1.10 m. After a week, all 24 measurements were repeated in an identical manner after disasssembling and reassembling of the entire setup.
The participants were recorded while seated in a chair with their back supported but without head support, in front of the cameras with a plain grey screen as a background. No facial landmarks were marked. The subject’s distance to the cameras was approximately 1 m and allowed displaying the entire chessboard. This was necessary for calibration and obtaining a large image of the face.
After calibration of the system with the chessboard, the participants were filmed at rest followed by a posed smile and then an aggressive smile. One video sequence was recorded per subject. For each of the 3 facial expressions, 2 frames were selected manually for analysis. The time lag between the 2 frames for each expression did not exceed 1 second.
The recordings were repeated after 8 weeks to test biologic intraindividual variability. The recording sessions did not exceed 2 minutes.
To investigate the validity of the method, all 16 participants had their intercanthal distance (Rc-Lc clin) clinically measured twice with the calipers.
Statistical analysis
Statistical analyses were performed by using Stata statistical software (release 10.1, Stata, College Station, Tex). The level of significance (α) was set at 5% ( P <0.05). The normal distribution of the values was tested with skewness-kurtosis tests.
To determine the system’s accuracy, the video measurements were compared with the real size of the chessboard squares by using a 1-sample t test. Therefore, the repeated measurements were averaged, and the 3 frames were analyzed individually. The systematic error was calculated by subtracting the real value from the digital value. Furthermore, the relative error was calculated as the percentage of the measured distances.
The precision was expressed as the difference between the 2 recordings at consecutive sessions. An analysis of variance (ANOVA) test and a multiple linear regression analysis were performed to look for effects of the frame, the repetitions, the positions of the chessboard, and the distances of the cameras. Finally, 95% CI values for the digital measurements were calculated.
The image analysis comprised digital measurements of the following distances ( Fig 3 , Table I ): at rest, intercanthal distance (Rc-Lc), distance endocanthion and oral commissure on the right (Rc-Rco), distance endocanthion and oral commissure on the left (Lc-Lco), and width of the mouth (Rco-Lco); on the aggressive smile, Rco-Lco; on the posed smile, Rco-Lco.
| Distance obtained clinically with calipers | |
| Rc-Lc clin | Mean value of 2 measurements of the intercanthal distance |
| Distances obtained off-line with the SmartEye system | |
| Resting position | |
| Rc-Lc V1-1 | Intercanthal distance: first recording, first frame (V1-1) |
| Rc-Lc V1-2 | Intercanthal distance: first recording, second frame (V1-2) |
| Rc-Lc V1 | Mean of Rc-Lc V1-1 and Rc-Lc V1-2 |
| Rc-Lc V2-1 | Intercanthal distance: second recording, first frame (V2-1) |
| Rc-Lc V2-2 | Intercanthal distance: second recording, second frame (V2-2) |
| Rc-Lc V2 | Mean of Rc-Lc V2-1 and Rc-Lc V2-2 |
| Rc-Rco V1-1 | Distance endocanthion and oral commissure on the right (V1-1) |
| Rc-Rco V1-2 | Distance endocanthion and oral commissure on the right (V1-2) |
| Rc-Rco V1 | Mean of Rc-Rco V1-1 and Rc-Rco V1-2 |
| Rc-Rco V2-1 | Distance endocanthion and oral commissure on the right (V2-1) |
| Rc-Rco V2-2 | Distance endocanthion and oral commissure on the right (V2-2) |
| Rc-Rco V2 | Mean of Rc-Rco V2-1 and Rc-Rco V2-2 |
| Lc-Lco V1-1 | Distance endocanthion and oral commissure on the left (V1-1) |
| Lc-Lco V1-2 | Distance endocanthion and oral commissure on the left (V1-2) |
| Lc-Lco V1 | Mean of Lc-Lco V1-1 and Lc-Lco V1-2 |
| Lc-Lco V2-1 | Distance endocanthion and oral commissure on the left (V2-1) |
| Lc-Lco V2-2 | Distance endocanthion and oral commissure on the left (V2-2) |
| Lc-Lco V2 | Mean of Lc-Lco V2-1 and Lc-Lco V2-2 |
| Rco-Lco VR1-1 | Distance between oral commissure left and right (V1-1) |
| Rco-Lco VR1-2 | Distance between oral commissure left and right (V1-2) |
| Rco-Lco VR1 | Mean of Rco-Lco V1-1 and Rco-Lco V1-2 |
| Rco-Lco VR2-1 | Distance between oral commissure left and right (V2-1) |
| Rco-Lco VR2-2 | Distance between oral commissure left and right (V1-2) |
| Rco-Lco VR2 | Mean of Rco-Lco V2-1 and Rco-Lco V2-2 |
| Posed smile | |
| Rco-Lco VP1-1 | Distance between oral commissure left and right (V1-1) |
| Rco-Lco VP1-2 | Distance between oral commissure left and right (V1-2) |
| Rco-Lco VP1 | Mean of Rco-Lco V1-1 and Rco-Lco V1-2 |
| Rco-Lco VP2-1 | Distance between oral commissure left and right (V2-1) |
| Rco-Lco VP2-2 | Distance between oral commissure left and right (V2-2) |
| Rco-Lco VP2 | Mean of Rco-Lco V2-1 and Rco-Lco V2-2 |
| Aggressive smile | |
| Rco-Lco VA1-1 | Distance between oral commissure left and right (V1-1) |
| Rco-Lco VA1-2 | Distance between oral commissure left and right (V1-2) |
| Rco-Lco VA1 | Mean of Rco-Lco V1-1 and Rco-Lco V1-2 |
| Rco-Lco VA2-1 | Distance between oral commissure left and right (V2-1) |
| Rco-Lco VA2-2 | Distance between oral commissure left and right (V2-2) |
| Rco-Lco VA2 | Mean of Rco-Lco V2-1 and Rc-Lco V2-2 |
The landmarks were selected according to the suggestions of Houstis and Kiliaridis.
For each analyzed distance, the mean values of 2 frames per recording were calculated. After we confirmed normal distribution, we tested the mean values of the first recording against the mean values of the second recording using the paired t test. The 95% CI values were also calculated.
The mean of the 2 clinical measurements of intercanthal distance with calipers was calculated (Rc-Lc clin). After we confirmed normal distribution, Rc-Lc clin was tested against the mean values obtained from the first (Rc-Lc VR1) and the second (Rc-Lc VR2) recording. Bland-Altman plots were created to show agreement between the clinical and video measurements.
Results
Normal distribution was confirmed for all measured values.
The digital measurements for the straight and diagonal distances of 2 vertically adjacent chessboard squares were statistically different from the real values (vertical side length, 60 mm; hypotenuse √7200, 84.853 mm [rounded]) ( Table II ).
| Frame 1 straight | Frame 2 straight | Frame 3 straight | Frame 1 diagonal | Frame 2 diagonal | Frame 3 diagonal | |
|---|---|---|---|---|---|---|
| P value | 0.009 ∗ | 0.008 ∗ | 0.028 ∗ | <0.001 ∗ | 0.018 ∗ | 0.327 |
| Mean absolute error (mm) | −0.227 | −0.153 | −0.212 | −0.179 | −0.161 | −0.054 |
| SD (±) | 0.39 | 0.26 | 0.44 | 0.22 | 0.31 | 0.23 |
| Relative difference (%) | 0.38 | 0.26 | 0.35 | 0.21 | 0.19 | 0.06 |
A systematic error in the measurements was detected. The minimum mean absolute error for square length was −0.153 mm (± 0.26 mm), whereas the maximum was −0.227 mm (± 0.39 mm). For the diagonal measurements, the minimum mean absolute error was 0.054 mm (± 0.24 mm), and the maximum was −0.179 mm (± 0.22 mm).
The 1-sample t test showed P values between 0.0083 and 0.0275 for the 60-mm distance, and between 0.0006 and 0.3268 for the diagonal distance when testing the measurements against the real values ( Table II ).
The ANOVA test and the multiple linear regression for the vertical measurements showed that position 4 and the second repetition influenced the results significantly (position 4, inclination of the chessboard of 15° in the y- and z-axes). Measurements in the position 4 underestimated the distances by a mean of 0.413 mm ( P <0.001). During the second repetition, the mean value was 0.158 mm smaller ( P = 0.046). There was no effect of the frame ( P = 0.706) or of the chosen distance from the cameras ( P = 0.782).
These effects were not present in the measurements of the squares’ hypotenuse. The 95% CI for the side-length measurements fluctuated around zero when the values of the second measurement and position 4 were omitted ( Figs 4 and 5 ).
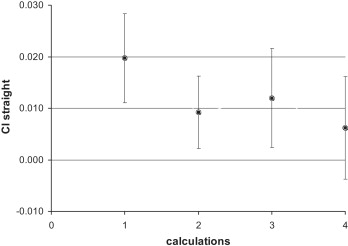
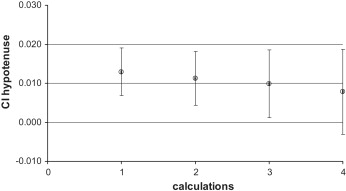
The mean values for repeated measurements in 1 recording are listed in Table III . The statistical analysis showed significant differences between the 2 analyzed frames for Rc-Lc V2-1 vs V2-2, Lc-Lco V2-1 vs V2-2, and Rco-Lco V2-1 vs V2-2. No significant difference was found when the mean of 2 frames of 1 recording was tested against the mean of 2 frames of the other recording for each distance. This effect was demonstrated for all measured distances ( Table IV ). The 95% CI for the measurements at rest were narrow and fluctuated around zero. For the aggressive and the posed smiles, the 95% CI values were wide but still fluctuated around zero ( Fig 6 ). The reproducibility of the mean values of the face at rest was between 0.04 mm (± 1.21 mm) for mouth width and 0.14 mm (± 0.46 mm) for intercanthal distance. For the dynamic face expressions, the reproducibility values were −1.36 mm (± 4.03 mm) (posed smile) and −0.47 mm (± 2.09 mm) for the aggressive smile ( Table IV ).
| Subject | Rc-Lc clin | Rc-Lc V1 | Rc-Rco V1 | Lc-Lco V1 | Rco-Lco VA1 | Rco-Lco VR1 | Rco-Lco VP1 | Rc-Lc V2 | Rc-Rco V2 | Lc-Lco V2 | Rco-Lco VA2 | Rco-Lco VR2 | Rco-Lco VP2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 35.20 | 34.87 | 70.11 | 69.82 | 69.48 | 53.47 | 64.22 | 34.77 | 70.05 | 69.49 | 63.75 | 53.52 | 61.28 |
| 2 | 33.84 | 34.98 | 64.41 | 64.69 | 67.00 | 49.79 | 61.39 | 34.26 | 64.51 | 63.89 | 67.56 | 48.41 | 64.62 |
| 3 | 31.12 | 31.80 | 74.67 | 73.38 | 55.53 | 51.69 | 70.38 | 31.87 | 73.51 | 72.05 | 58.29 | 52.39 | 65.38 |
| 4 | 28.07 | 28.64 | 67.86 | 66.16 | 63.17 | 48.60 | 64.21 | 28.01 | 68.89 | 67.53 | 64.47 | 49.40 | 63.59 |
| 5 | 30.57 | 30.88 | 64.85 | 64.67 | 61.51 | 48.11 | 58.82 | 30.60 | 65.28 | 65.42 | 62.53 | 46.86 | 58.42 |
| 6 | 32.48 | 31.95 | 58.55 | 58.25 | 71.73 | 53.46 | 69.42 | 32.19 | 60.02 | 58.19 | 71.90 | 51.77 | 70.46 |
| 7 | 29.72 | 29.22 | 64.91 | 66.24 | 66.26 | 52.98 | 66.78 | 30.22 | 65.63 | 67.49 | 65.89 | 51.56 | 70.64 |
| 8 | 30.86 | 30.37 | 65.14 | 65.27 | 61.29 | 44.43 | 56.99 | 30.46 | 64.96 | 64.42 | 63.54 | 43.57 | 60.40 |
| 9 | 30.33 | 32.07 | 68.61 | 69.33 | 66.63 | 48.25 | 68.23 | 31.78 | 68.19 | 69.01 | 69.95 | 48.67 | 68.31 |
| 10 | 33.55 | 33.95 | 67.48 | 68.38 | 67.38 | 45.41 | 52.72 | 33.26 | 66.45 | 68.37 | 66.18 | 47.42 | 62.18 |
| 11 | 30.10 | 30.30 | 58.54 | 58.50 | 72.15 | 51.23 | 74.67 | 29.87 | 58.61 | 58.47 | 72.44 | 50.58 | 74.66 |
| 12 | 33.48 | 32.97 | 58.29 | 58.16 | 64.65 | 50.85 | 65.80 | 32.53 | 57.30 | 57.79 | 65.87 | 52.40 | 67.61 |
| 13 | 28.26 | 28.20 | 65.35 | 63.48 | 63.15 | 47.55 | 63.16 | 28.50 | 66.25 | 64.19 | 62.59 | 47.08 | 61.76 |
| 14 | 31.41 | 31.98 | 60.31 | 58.29 | 66.27 | 53.14 | 65.60 | 31.47 | 59.35 | 57.49 | 67.55 | 52.49 | 68.26 |
| 15 | 34.94 | 35.73 | 70.30 | 69.65 | 78.08 | 54.67 | 67.55 | 35.47 | 69.34 | 68.18 | 80.06 | 56.67 | 77.08 |
| 16 | 34.81 | 34.65 | 64.28 | 62.59 | 68.14 | 53.90 | 64.38 | 34.98 | 63.14 | 62.80 | 67.33 | 54.09 | 61.40 |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


