In a case-control study, a group of subjects from a specified study population who have the outcome of interest (the cases)—eg, patients with temporomandibular joint (TMJ) pain—is identified, and a control group is then identified of those without the outcome of interest (the controls).
Information is then collected from the cases and the controls on their past exposure or exposures. This information can be taken from sources such as interviews and medical records. Then the numbers of exposed and unexposed subjects within the cases and controls are compared; if there are important differences, then the exposure might be a risk factor for the disease. A diagrammatic representation of a case-control study is shown in the Figure .
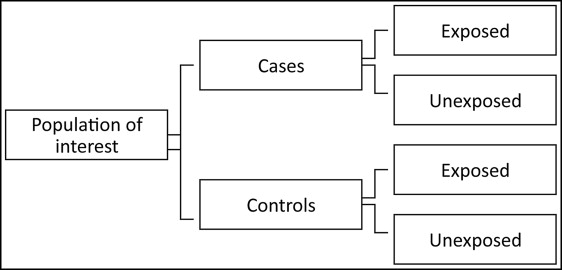
The case-control design and method of analysis were developed to investigate risk factors for diseases with long latent periods, when implementation of cohort studies is impractical. A classic example is the case-control study on the association between smoking and lung cancer.
A relevant example could be the examination of the association between TMJ pain and trauma from a blow to the chin, or TMJ pain and orthodontic therapy. Cases and controls can be identified, and their exposure to trauma or orthodontic therapy ascertained. If the odds of exposure to trauma (or orthodontic therapy) are higher in the TMJ pain group, then an association between the exposure and the outcome might be implied. Tables I and II show the results of this hypothetical case-control study. Remember that the odds are defined as the number of exposed divided by the number of unexposed for the case and control groups. In these tables, we can see that the odds of exposure are 3 (600/200) among the cases and 1.125 (900/800) among the controls. The odds ratio is a measure of relative risk and is usually calculated by dividing the odds of exposure among the cases by the odds of exposure among the controls (3/1.125 = 2.67) or, less commonly, 1.125/3 = 0.375. At the end of Table I , a statistical test indicates that we have a statistically significant finding (χ 2 [1] = 10.46 Pr > χ 2 = 0.001). However, whether trauma is a risk factor will depend on bias, the distribution of other factors (confounding), and whether the relationship is causal.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


