Material and methods

We measured the mesiodistal angulation of the typodont teeth with the coordinate measuring machine (Faro International, Lake Mary, Fla). The typodont was based on a modification of the model previously reported by McKee et al and Garcia-Figueroa et al. It consisted of transparent plastic anatomic typodont maxilla and mandible (Kilgore International, Coldwater, Mich) with synthetic teeth in idealized occlusion from the second molar to the second molar. As shown by Van Elslande et al, the typodont was mounted on a dry human skull. Stainless steel balls (Small Parts, Miramar, Fla), 1.58 mm in diameter, were placed at the approximate mesiodistal and faciolingual centers of the occlusal surfaces, and at the approximate centers of the root apices for single-rooted teeth or the centers of the bifurcation or trifurcation at the level of the root apices for multi-rooted teeth. A line connecting the 2 centers on each tooth represented its long axis.

The coordinate measuring machine was used to determine the actual mesiodistal angular measurement of each whole tooth with reference to the archwires that were held in place on the plastic molds of the maxilla and the mandible at approximately the middle of the roots. A mesiodistal plane was created for each tooth that was perpendicular to the horizontal (archwire) plane. This tooth-specific reference plane passed through the mesial and distal interproximal points marked on the archwires with crimpable stops. The mesiodistal angulation of a tooth was the measurement of the angulation between the projection of the tooth’s long axis on the mesiodistal plane and the vertical line.

One investigator (D.V.E.) made repeated measurements on 5 separate occasions, 5 days apart, and the intraclass correlation coefficient values were calculated to determine the reliability of the coordinate measuring machine’s angulation measurements. The coordinate measuring machine was reported by the manufacturer to be accurate to within 0.013 mm. For angular measurements, the machine was found to be accurate to within 0.031°. The average of the 5-time repeated coordinate measuring machine’s angulation measurements were used as the true values.

The typodont teeth’s mesiodistal angulations and faciolingual inclinations were also measured by using the custom USC root vector analysis program. For the CBCT scan of the same typodont used above, a NewTom 3G volume scanner (AFP, Elmsford, NY) was used according to the manufacturer’s instructions as shown also by Van Elslande et al. Twenty-five independent images were obtained from separate CBCT scans for the previous study, and 5 of them were randomly selected and imported into the Dolphin Imaging 3D program. The USC root vector analysis program was developed in the Dolphin 3D module to measure both the mesiodistal angulation and the faciolingual inclination of each whole tooth as shown below.

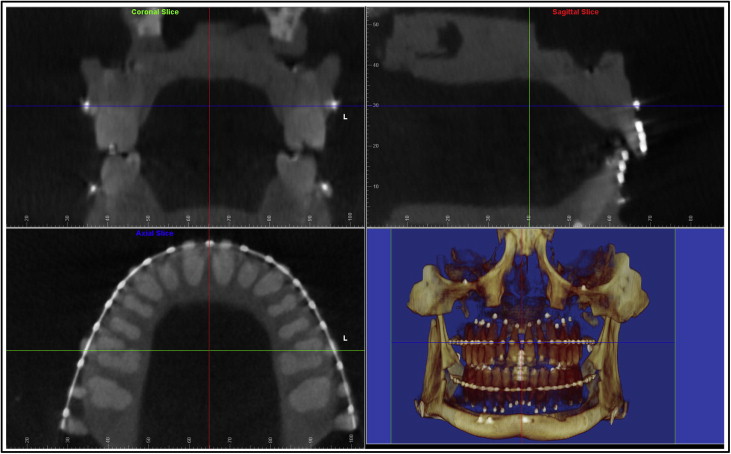
Once the typodont digital imaging and communications in medicine (DICOM) data were imported into Dolphin 3D, a 3-dimensional global coordinate system was first generated for the proper orientation of the head and the maxillofacial structures. This coordinate system included the midsagittal plane, the coronal plane, and the axial plane, each perpendicular to the other 2 planes ( Fig 1 ). The midsagittal plane evenly divided the right and the left halves of the skull; the coronal plane passed through the maxillary first molar buccal grooves on both sides, and the axial plane was the archwire plane. Since the maxillary and mandibular teeth had separate archwire planes, there were also 2 separate 3-dimensional global coordinates: 1 saved for the maxilla, and 1 saved for the mandible.

Setting up the global coordination system for the maxillary arch: the midsagittal plane ( red ) evenly dividing the right and left sides, the coronal plane ( green ) at the buccal groves of the maxillary right and left first molars, and the axial plane ( blue ) at the maxillary archwire level.

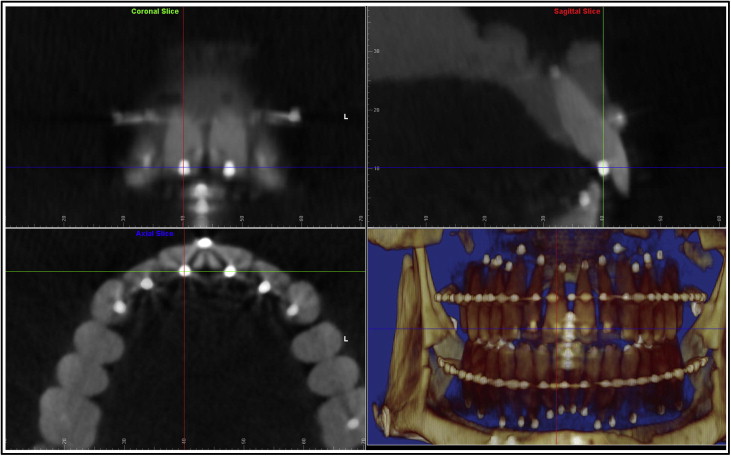
The digitization of each tooth’s long axis was done in all 3 plane views, each perpendicular to the other 2 views. Parallel movements of the sagittal, coronal, and axial planes were made so that each would pass through the center of the white stainless steel marker representing either the crown or the root point of each tooth ( Figs 2 and 3 ). A red dot was digitized at the intersection of the 3 perpendicular planes in 1 of the 3 plane views; it would also appear automatically in the other 2 views. The order of digitization was from the maxillary right second molar to the maxillary left second molar, and from the mandibular left second molar to the mandibular right second molar. Figure 4 shows all the white stainless steel markers replaced by the red digitization points. The green lines represented the long axes of the teeth after the digitization was completed in both arches.

Locating the maxillary right central incisor crown point before digitization: parallel movements of the sagittal ( red ), coronal ( green ), and axial ( blue ) planes were made to intersect at the center of the stainless steel ball representing the tooth’s crown point.

Digitization of the maxillary right central incisor root point: parallel movements of the sagittal ( red ), coronal ( green ), and axial ( blue ) planes were made to intersect at the center of the stainless steel ball representing the tooth’s root point, and it was digitized ( red dots ).

All crown and root points have been replaced by red digitization dots, and the teeth’s long axes are shown in green .

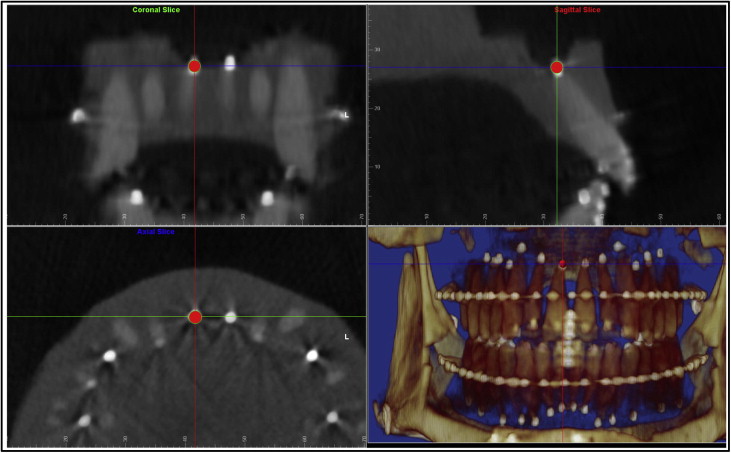
Next we digitized the archwires. For the maxillary arch, the global coordinate saved for the maxillary teeth was restored first, and the maxillary archwire was digitized in the axial plane view set at the archwire level ( Fig 5 ). Four teeth on the right side were digitized along the archwire: midincisor, canine, second premolar, and second molar. The software program would add the mirror image of the right side half arch to the left side, constructing a symmetrical arch form. The mandibular archwire was digitized in the same way after the global coordinate saved for the mandibular arch was restored.

The maxillary arch on the right side was digitized based on 4 points along the archwire relative to the following tooth positions: midincisor, right canine, right second premolar, and right second molar ( yellow dots ). The left side half arch was the mirror image of the right side half. The tooth-specific coordinate system was based on the arch form and the crown point of each tooth: the transverse plane was the maxillary archwire plane; the faciolingual plane ( long straight green line ) passed each tooth crown point ( dark blue dot ) and was perpendicular to the maxillary arch; the mesiodistal plane ( short light blue line ) was perpendicular to the faciolingual plane at the crown point ( dark blue dot ) of each tooth.

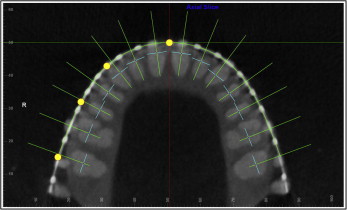
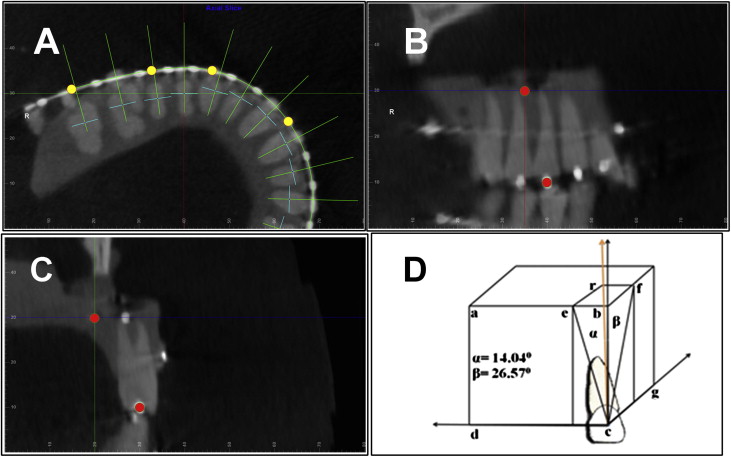
Then the tooth-specific coordinate system for the mesiodistal angulation and the faciolingual inclination measurements was set up. Once the arch form was digitized, the custom USC root vector analysis program would automatically construct another 3-plane coordinate system consisting of multiple coordinates, each specific for only 1 tooth for its mesiodistal angulation and faciolingual inclination measurements ( Fig 5 ): the transverse plane was the same axial plane at either the maxillary or the mandibular archwire level as in the global coordinate system; the straight green line represented the faciolingual plane that passed through each tooth crown point (dark blue dot) and was perpendicular to the archwire; the short light blue line represented the mesiodistal plane that also passed through each tooth crown point, but was perpendicular to the faciolingual plane. The mesiodistal angulation and the faciolingual inclination were measured for each tooth in its corresponding tooth-specific coordinate.

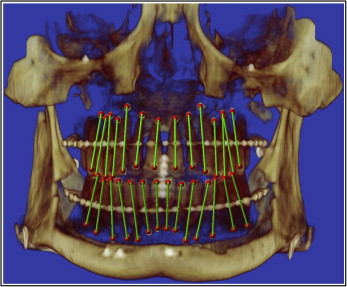
As shown in Figure 6 , A , the mesiodistal angulation was measured from the projection of the tooth’s long axis on the mesiodistal plane to the vertical line formed by the intersection of the mesiodistal and faciolingual planes. If the root center was distal to the crown center, the measurement would be positive; otherwise, it would be negative. The faciolingual inclination was measured from the projection of the tooth’s long axis on the faciolingual plane to the vertical line formed by the same intersection of the mesiodistal and faciolingual planes ( Fig 6 , B ). If the root center was lingual to the crown center, the measurement would be positive; otherwise, it would be negative.

A, Mesiodistal angulation was measured in the mesiodistal plane and defined as the angle formed by the projection of the tooth’s long axis ( green line ) and the red line that represented the faciolingual plane and the mesiodistal plane intersection; B, faciolingual inclination was measured in the faciolingual plane and defined as the angle formed by the projection of the tooth’s long axis ( short green line ) and the long green line that represented the mesiodistal plane and the faciolingual plane intersection. The blue line in A and B represented transverse planes that were parallel to the occlusal plane.

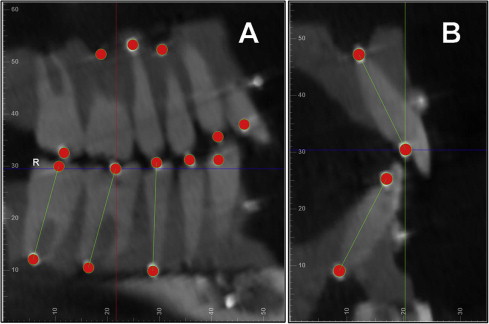
At this point, the custom USC root vector analysis program would use algorithms to measure the mesiodistal angulation and the faciolingual inclination values for all teeth automatically.

Teeth with known mesiodistal angulation and faciolingual inclination values were measured. The same 5 typodont images above were used again, except that the root points of the maxillary right first molar and first premolar, the maxillary left central incisor and second molar, the mandibular right second molar and canine, and the mandibular left lateral incisor and first molar were not digitized at the stainless steel balls representing the apices of these teeth but at locations defined through the following three steps ( Fig 7 ): (1) in the axial slice view ( Fig 7 , A ) at the crown point level, the image was rotated so that for the tooth to be digitized, the faciolingual direction was shown vertically and the mesiodistal direction was shown horizontally; (2) in the mesiodistal ( Fig 7 , B ) or faciolingual ( Fig 7 , C ) slice view, the transverse plane at the crown point level was moved 20 mm apically; and (3) in the mesiodistal slice view ( Fig 7 , B ), the faciolingual plane was moved 5 mm distally, and in the faciolingual slice view ( Fig 7 , C ), the mesiodistal plane was moved 10 mm lingually. After these parallel movements of the reference planes, the 3-plane intersection would be at a point that was 20 mm apical, 10 mm lingual, and 5 mm distal from the crown point. The root point was digitized at this intersection. Trigonometric calculation should give the tooth 14.04° of mesiodistal angulation and 26.57° of faciolingual inclination. For the maxillary right first molar and the mandibular left lateral incisor, the root points were placed mesially instead of distally to reflect their distal angulation; for the 2 mandibular molars, the root points were placed buccally instead of lingually to reflect their lingual crown inclinations.

Digitization of the root point for the known mesiodistal angulation and faciolingual inclination. A, Set the axial view at the maxillary archwire level, then move the transverse plane to the crown point level for the maxillary right first premolar to be digitized, rotate the image in the axial view so that the faciolingual direction of the tooth was shown vertically and the mesiodistal direction was shown horizontally. B, The mesiodistal plane view showing that the transverse plane ( blue ) was moved 20 mm apically, and the faciolingual plane ( red ) was moved 5 mm distally from the crown point. C, The faciolingual plane view showing that the mesiodistal plane ( green ) was moved 10 mm lingually. The intersection of the transverse plane ( blue ), the mesiodistal plane ( green ), and the faciolingual plane ( red ) was where the root point was digitized. D, Diagram showing the 3-dimensional relationship: a, b, c, d, and g each at a corner of a cubic with each side 20 mm long. The center of the crown is placed at point c . cd points mesiodistally; cg points faciolingually, and cb points occlusogingivally; cb , 20 mm apical; be , 5 mm distal; bf , 10 mm lingual; r , designated root point; and yellow arrow , presumed long axis of the tooth. The mesiodistal angulation α and the faciolingual inclination β for the tooth were calculated to be 14.04° and the 26.57°, respectively.