Introduction
The aim of this study was to describe a natural and anatomic lingual arch form obtained from subjects with normal occlusion that could be used, with other criteria, in the construction of personalized setups for the lingual straight-wire technique.
Methods
The study sample comprised 58 pairs of dental casts of the arches of 58 southern Europeans (37 women, 21 men) with ideal natural occlusions. After the reference points of the dental arches were identified and marked, the dental casts were scanned. The exact position of the models on the scanner was established by using an acetate sheet with a Cartesian reference system. For each image, 14 reference points (x, y) were measured and recorded. The measurements were processed with software to select the polynomial function that best described the shape of the dental arches. The ninth-degree polynomial function was selected to represent the lingual arch form of both arches. Distribution analysis of the x and y values of each tooth in each arch resulted in the creation of 3 groups (small, medium, and large) to verify the most appropriate measures of the central tendencies of our data.
Results
Statistical analysis showed no significant sex difference in the medians of the 6 parameters used to measure depth and width in both arches. A representation of the variability of the lingual curve of our sample was created to document at least 3 sizes of the representative curve of the central tendency for our data. No statistically significant differences in shape were found between men and women, considering the medians as a measure of the central tendencies.
Conclusions
Three lingual curves (small, medium, and large) for the maxillary and mandibular arches, representing the mean values of our sample, were developed and can be used as guides for the setup in the lingual straight-wire technique.
The form of the dental arch is considered a fundamental element in orthodontic diagnosis and treatment planning because of its ability to influence not only available space and dental and smile esthetics, but also long-term occlusal stability. Furthermore, respecting this important parameter reduces the possibility of crowding relapse and periodontal damage. Moreover, definition of the shape of the arch aids the clinician in achieving results that agree with the natural laws of biologic variability. Andrews, father of the labial straight-wire technique, cited the arch form as the seventh of his keys to achieving Class I occlusion. Hence, in recent decades, numerous studies have analyzed the arch form from anatomic and anthropologic perspectives to evaluate its implications in orthodontic therapy or its modifications after orthodontic treatment.
Even though the necessity of individualizing each patient’s arch form during treatment is widely recognized, after the evolution of labial straight-wire appliances and because of the superelastic properties of the latest generation of archwires, it seems to be clinically reasonable to stereotype the constructed arch shapes from subjects with normal occlusion into a few sets of preformed arches. The most similar to that of the patient before treatment could therefore be selected on the basis of geometric similarity, ethnicity, and type of malocclusion. Nevertheless, no objective study has thus far elucidated the choice of a particular arch form, although various studies have sought, by using the incisal and occlusal margins of the teeth as anatomic reference points, to represent it graphically from the labial side. Numerous authors used geometric curves to describe the dental arch. Moreover, various authors have observed that polynomial functions can simply and symmetrically describe the shape of the dental arch, and have exploited these mathematic equations as an accurate method for its description.
Many articles in the literature have dealt with the shape of the dental arch from the labial perspective, although nothing has yet been published regarding the lingual side. Many systems for representing the normal arch form have been proposed, including qualitative descriptions, geometric constructions, and mathematic curves; although there is consensus on the importance of this factor in orthodontics, a definitive geometric shape is elusive, as demonstrated recently by Triviño et al.
However, the introduction of the straight-wire to the lingual technique and the possibility of replacing Fujita’s “mushroom form” with an arch form without insets has led to the question of which arch form to choose and which criteria to use in the lingual straight-wire setup and treatment planning. Because a “straight” arch form has not previously been described from a lingual perspective and this is fundamentally important in orthodontic treatment planning, in this study it is described with an objective, standardized, and reproducible methodology: a natural and anatomic arch form obtained from subjects with normal occlusion. This can be used, with other criteria, in the construction of personalized setups for the lingual straight-wire technique.
Material and methods
The sample was carefully selected from the records of the University of Ferrara Postgraduate School of Orthodontics in Italy and the Department of Orthodontics at the Complutense University of Madrid, Spain. It included southern European white adults with the following characteristics : (1) age not less than 18 years (range, 19.08-70.25 years); (2) no previous orthodontic treatment; (3) regular arch form with little or no crowding; (4) complete dentition up to at least the second molars; (5) no extensive restoration and implants; (6) at least 4 of the 6 Andrews’ keys for optimal occlusion and bilateral Class I molar and canine relationship; (7) normal (within 2 ± 1 mm) overbite and overjet; (8) no deviations of the interincisal lines; (9) no gingival recession; (10) no muscular or joint pathologies; (11) no ectopic teeth, tooth aplasia, or anomalies in tooth shape; (12) no supernumerary or congenitally missing teeth; (13) no anterior or posterior crossbite; (14) no visible intraoral or extraoral asymmetry; and (15) minimal diastemas, premolar rotations, and incisor irregularities (present in several subjects). Each subject participating in the study gave informed written consent.
Mandibular and maxillary dental casts of each subject, according to Tweed prescriptions, were obtained, for a total of 75 pairs. The regularity of these models was first determined clinically and then quantified by using Little’s irregularity index ; 9 pairs of models had a value greater than 3 and were therefore excluded, as were a further 8 pairs, which, although having a value less than 3, had spaces greater than 1 mm or a slightly asymmetrical contraction of the arch in the premolar area. Thus, the definitive sample comprised 58 pairs of dental casts of the arches of 58 white subjects (37 women, 21 men) of southern European ancestry (mainly Italian and Spanish). The mean age of the sample was 29.21 years (SD, 8.73 years); the youngest was 19.08, and the oldest was 70.25 years of age.
Reference points for calculation of the shape of the arch were identified and marked on the lingual surface of each tooth (from the left second molar to the right second molar) of each dental cast by 1 operator (L.S.) using an indelible marker (.08-mm Pilot drawing pen; Pilot Corp., Tokyo, Japan). In the mandibular arch, these points, which trace the lingual straight plane, were situated at the center of the clinical crown (vertical position) along the central lingual axis and at the most prominent point on the lingual surface of each tooth (horizontal position) on the molars and premolars and corresponding to the middle third of the anterior teeth. In the maxillary arch, the reference points were marked at the most prominent point on the lingual surface of each tooth (horizontal position) at the intersection between the middle third and the gingival third of the anterior teeth, along their central axes, and at the center of the clinical crown of the posterior teeth. Before permanently marking these points on the lingual surface, the median axis of the clinical crown of each tooth was traced in pencil to determine its horizontal position, and a gauge was used to measure the height of the clinical crown to determine its vertical position. Although the same operator carried out this procedure for each tooth, it was an important source of error, because the accuracy of identification of the reference points necessarily influences the tracing of the curves on which the calculations of arch shape are based.
After the reference points had been marked, the dental casts were scanned with an Expression 1680 Pro scanner (Epson, Cinisello, Balsamo, Italy), and images in TIF format at a resolution of 300 dpi were obtained. To avoid distortion of the image, and hence the reference points, during the scanning procedure, the models were positioned so that both the base and the occlusal plane were parallel to the scanner’s surface. The exact position of the models on the scanner was established with a specially created acetate sheet onto which a sheet of millimeter paper had been photocopied. After the photocopies were made, the prepared acetate and millimeter papers were superimposed to verify the lack of distortion in the acetate copy. On this acetate sheet, reference axes—a horizontal line and a perpendicular vertical line—were drawn with an indelible marker (.05-mm Pilot drawing pen). The sheet was subsequently placed on the glass surface of the scanner under the plaster models to align the posterior margin of the second molars with the abscissa and the median line with the ordinate, thus creating a Cartesian reference system ( Fig 1 ).
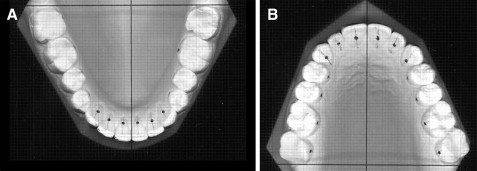
For each image, 14 reference points, corresponding to the distance between each reference point and the abscissa and ordinate were measured and recorded to provide their Cartesian coordinates (x, y).
Four weeks later, to calculate the method error, 15 models were selected at random, and the coordinates of each reference point on both arches were replotted by the same operator as above. Analysis of the reliability of measurements was performed by using Dahlberg’s coefficient, Se = √∑d2/2n, where S is the Dahlberg coefficient, d is the difference between the first and second measurements, and n is the number of repeated measurements.
The values corresponding to the coordinates of the central and lateral incisors and the second premolars were compared singly with their control measurements. The statistical significance was evaluated by using the Student t test for paired data. The systematic error of measurement of each value considered was shown to be not significant at P = 0.05, thereby confirming the reliability of the results.
First, the dimensions of both dental arches were evaluated via 3 transversal and 3 sagittal measurements: the transverse diameters and arch depths at the canines, first molars, and second molars, as described by Raberin et al. The lingual reference points considered were (1) the interincisor point; (2) the most prominent point on the central axis of the lingual surface of the canine crown; (3) the most prominent point on the lingual surface of the first molar at the center of its clinical crown; and (4) the most prominent point on the lingual surface of the second molar at the center of its clinical crown.
Thus, 6 measurements of distance were taken for each arch to analyze their width and depth. To measure arch width, the following were considered: intercanine diameter (D3), intermolar diameter at the first molars (D6), and intermolar diameter at the second molars (D7).
To measure the arch length, the following were considered: (1) canine depth, the distance between the interincisor point and the line connecting the canine reference points (L3); (2) molar depth at the first molars, the distance between the interincisor point and the line connecting the reference points on the first molars (L6); and (3) molar depth at the second molars, the distance between the interincisor point and the line connecting the reference points on the second molars (L7).
Subsequently, the shape of the dental arch was evaluated from the lingual side. The measurements (x and y coordinates) of each reference point were all obtained and processed by using Curve Expert software (version 1.3, http://curveexpert.webhop.biz ) by the same operator. This software was used to select the polynomial function that best described the shape of the dental arches.
After the dental arches were viewed and the presence of slight asymmetry was established, even though patients with normal occlusion had been used as models, the reference point coordinates of the 58 dental casts were divided into the left and right sides.
Each arch half, described by 7 reference points (7 x and y coordinates), was then “mirrored” to obtain 116 whole maxillary and 116 whole mandibular arches with symmetrical curves.
Based on the number of reference points (7 for each semiarch mirrored) and after the graphs obtained of the various mathematical functions were viewed, the ninth-degree polynomial function was selected to represent the lingual surfaces of both arches.
This polynomial function yielded the curve most representative of the shape of the lingual dental arch. It was first selected according to visual inspection criteria, and then, to confirm this choice objectively, we determined which marker could be considered to establish the suitability of the model. With the residual analysis, we ascertained whether the observed values fell outside the trend of the expected curve.
The residual plot graphically depicts the difference between the data points and the model evaluated at the data points. The residual at point i is defined by residual = yi – f(x i ), where yi is the measured value at x i , and f(x i ) is the predicted value at x i . These distances are shown as bars or points on the residual plot; the magnitudes of the data points are simply replaced by the residual defined above. If the residual is positive, then the data point is above the model’s prediction; if the residual is negative, then the data point is below the model’s prediction. The residuals can provide an indication of a particular model’s performance. If there are runs of like-signed residuals, then a better model for the data is likely to exist.
Optimally, the residuals should show a random scatter around zero, which indicates that the data points are randomly distributed around the curve. A “run” is a sequence of like-signed residuals, which stand out on the residual plot. A large number of runs indicates that the data systematically deviate from the curve.
The critical reference measurement for a residual value is usually 1.96. If this value is exceeded at 1 point or more, the fit is unacceptable, and adaptations must be made. The measurement error was compared with the standard error values of various models to ascertain which model better interpolated the data—ie, that characterized by the lowest standard error was considered the best; in our case, it was the ninth-degree polynomial.
The standard error was calculated with minimization of the so-called merit function ( http://mathworld.wolfram.com/MeritFunction.html ).
Statistical analysis
The sample was initially subjected to descriptive statistical analysis including mean, standard deviation, variance, minimum, and maximum values.
The analysis of sexual dimorphism was carried out with a comparative analysis of the lingual distances D3-3, D6-6, D7-7, L3, L6, and L7 to verify whether there were statistically significant differences between the measures of the central trend in the men and women. Due to the abnormal distribution of data, the nonparametric Mann-Whitney U test was applied to compare the 2 independent groups.
To provide a visible representation of a hypothetical ideal arch form curve, first the means and standard deviations of the 14 coordinates of the abscissa and ordinate were calculated for all curves relative to the lingual sides of both arches. Three groups—small, medium, and large—were created by a distribution analysis of the x and y values of each tooth in each arch to verify the most appropriate measure of the central tendencies for our data. It was verified that all x and y values were characterized by strongly nonnormal, asymmetrical, and unimodal distributions. This led us to choose the median value as the reference measure of the central tendency, and then the values of the 25th (first quartile) and 75th (third quartile) percentiles as measures of variability. Assuming that the median was an adequate representation of the measure of the central tendencies for the medium group, the measures of the central tendency for the small and large groups were identified. The objective was to identify 3 curves, corresponding to the 3 groups, that interpolated the measures of central tendency in a parallel fashion. Because of the many anomalous values and the variability that characterized each tooth, it was not possible to consider the first and third quartiles as measures of the central tendency for each tooth in the small and large groups. Hence, the coordinates characterized by the minimum variability (x7, y1) were considered, and a maximum deviation around the median equal to 1 mm in both arches was identified. Thus the following measures were obtained.
-
Central tendency for x7 small = median (x7) – 1.
-
Central tendency for x7 large = median (x7) – 1.
-
Central tendency for y1 small = median (y1) – 1.
-
Central tendency for y1 large = median (y1) – 1.
Thus, the central tendency of the small and large groups for the other coordinates were obtained, applying the 1-mm displacement to the median of all x and y values. In this way, constant “distances” along all points of the mouth between the central tendency measures of the medium group and those of the small and large groups were created.
Results
The descriptive statistics of each of the 6 parameters used to measure depth and width, subdivided by arch and sex, are reported in Table I . The values for mean, median, minimum, maximum, 25th percentile, 75th percentile, and standard deviation are also reported.
| Mean | Median | Minimum | Maximum | Percentile 25 |
Percentile 75 |
SD | |
|---|---|---|---|---|---|---|---|
| Mandibles in men | |||||||
| D3-3 | 21.2 | 21 | 18 | 26 | 20 | 22 | 1.928 |
| D6-6 | 32.7 | 32 | 28 | 42 | 30 | 34 | 3.034 |
| D7-7 | 38.5 | 38 | 30 | 48 | 36 | 40 | 3.783 |
| L3 | 4.1 | 4 | 2 | 6 | 4 | 5 | 0.899 |
| L6 | 25.2 | 25 | 22 | 30 | 24 | 26 | 1.914 |
| L7 | 35.3 | 355 | 31 | 42 | 34 | 37 | 2.472 |
| Mandibles in women | |||||||
| D3-3 | 21.0 | 20 | 18 | 26 | 20 | 22 | 1.826 |
| D6-6 | 33.4 | 34 | 30 | 40 | 32 | 36 | 2.399 |
| D7-7 | 39.6 | 40 | 34 | 48 | 38 | 42 | 3.153 |
| L3 | 4.1 | 4 | 2.5 | 8 | 4 | 5 | 0.871 |
| L6 | 25.2 | 25 | 21 | 31 | 24 | 26 | 1.960 |
| L7 | 35.1 | 35 | 30 | 43 | 33 | 36 | 2.647 |
| Maxillae in men | |||||||
| D3-3 | 27.1 | 26 | 24 | 34 | 26 | 28 | 2.510 |
| D6-6 | 36.7 | 36 | 30 | 50 | 34 | 38 | 3.502 |
| D7-7 | 42.2 | 42 | 34 | 52 | 40 | 44 | 3.769 |
| L3 | 6.9 | 7 | 4 | 9 | 6 | 8 | 1.173 |
| L6 | 29.3 | 30 | 22.5 | 41 | 28 | 30.5 | 2.870 |
| L7 | 38.5 | 39 | 32 | 48 | 37 | 40 | 2.987 |
| Maxillae in women | |||||||
| D3-3 | 26.6 | 26 | 22 | 34 | 24 | 28 | 2.447 |
| D6-6 | 36.9 | 36 | 29 | 46 | 34 | 38 | 3.367 |
| D7-7 | 42.4 | 42 | 34 | 50 | 40 | 46 | 4.028 |
| L3 | 6.6 | 7 | 5 | 9 | 6 | 7 | 1.035 |
| L6 | 28.9 | 29 | 25 | 34 | 27 | 30 | 2.193 |
| L7 | 42.1 | 39 | 33 | 41 | 36 | 40 | 3.328 |
The results of the Mann-Whitney nonparametric U test are reported in Table II . The P values show no significant statistical sex difference for the medians measured in both arches.
| Variable | Rank sum for women |
Rank sum for men |
U | P value | N valid women |
N valid men |
|---|---|---|---|---|---|---|
| Mandible | ||||||
| D3-3 | 4273.5 | 2512.5 | 1498.5 | 0.752040 | 74 | 42 |
| D6-6 | 4584 | 2202 | 1299 | 0.143744 | 74 | 42 |
| D7-7 | 4598 | 2188 | 1285 | 0.122974 | 74 | 42 |
| L3 | 4156 | 2630 | 1381 | 0.321717 | 74 | 42 |
| L6 | 4272 | 2514 | 1497 | 0.745508 | 74 | 42 |
| L7 | 4163 | 2623 | 1388 | 0.341744 | 74 | 42 |
| Maxilla | ||||||
| D3-3 | 4158.5 | 2627.5 | 1383.5 | 0.328780 | 74 | 42 |
| D6-6 | 4387 | 2399 | 1496 | 0.741164 | 74 | 42 |
| D7-7 | 4401.5 | 2384.5 | 1481.5 | 0.679161 | 74 | 42 |
| L3 | 4083 | 2703 | 1308 | 0.158455 | 74 | 42 |
| L6 | 4132.5 | 2653.5 | 1357.5 | 0.260194 | 74 | 42 |
| L7 | 4146 | 2640 | 1371 | 0.294463 | 74 | 42 |
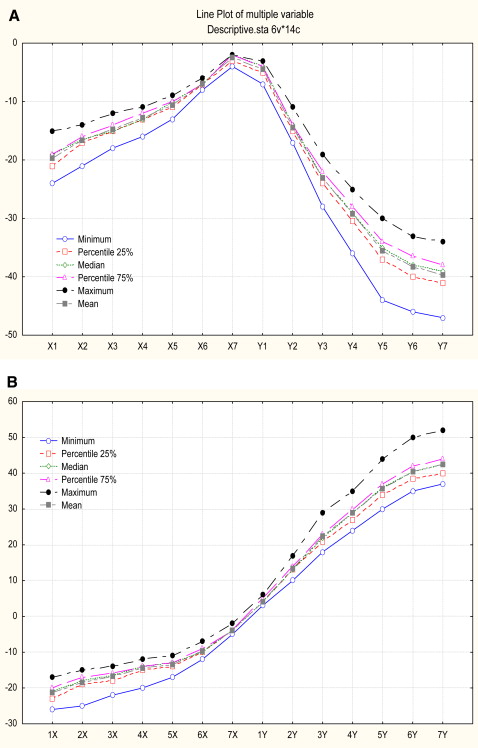
Initially, a simple graphic representation of the lingual side of the arch form was obtained by using the means and standard deviations of the coordinates for the maxillary and mandibular arches, respectively. Subsequently, a representation of the variability of the lingual curve of our sample was created to document at least 3 sizes of the representative curve.
Table III documents the descriptive statistics of the 14 coordinates corresponding to the reference points used to describe the curves that best represent the shapes of the arches, respectively. Figure 2 depicts the data in Table III ; it is possible to observe the difference in variation of the coordinates. Thus, the x and y coordinates that varied the least were considered, as shown in Table III . After identifying 1 mm as the constant measure to be subtracted and added to the median measures, the central tendencies relative to the small and large groups were obtained, as described in Table IV . Figure 3 shows the 3 curves, large, medium, and small, superimposed onto the scatter plot.
| Minimum | Percentile 25 |
Median | Percentile 75 |
Maximum | Mean | |
|---|---|---|---|---|---|---|
| Mandible | ||||||
| 1X | −24 | −20.5 | −19 | −19 | −15 | −19.67 |
| 2X | −21 | −17 | −16 | −16 | −14 | −16.58 |
| 3X | −18 | −15 | −14.25 | −14 | −12 | −14.62 |
| 4X | −16 | −13 | −13 | −12 | −11 | −12.78 |
| 5X | −13 | −11 | −10 | −10 | −9 | −10.53 |
| 6X | −8 | −7 | −7 | −6 | −5.5 | −6.84 |
| 7X ∗ | −4 | −3 | −2 | −2 | −2 | −2.45 |
| 1Y ∗ | −7 | −5 | −4.5 | −4 | −3 | −4.40 |
| 2Y | −17 | −15 | −14 | −13.5 | −11 | −14.31 |
| 3Y | −28 | −24 | −23 | −22 | −19 | −23.01 |
| 4Y | −36 | −30 | −29 | −28 | −24.5 | −29.19 |
| 5Y | −44 | −37 | −35 | −34 | −30 | −35.42 |
| 6Y | −46 | −40 | −38 | −36 | −33 | −38.15 |
| 7Y | −47 | −41 | −39 | −37.5 | −34 | −39.56 |
| Maxilla | ||||||
| 1X | −26 | −22.75 | −21 | −20 | −17 | −21.12 |
| 2X | −25 | −19 | −18 | −17 | −14.5 | −18.46 |
| 3X | −22 | −17.25 | −16 | −15.75 | −13.5 | −16.55 |
| 4X | −20 | −15 | −14 | −13.5 | −12 | −14.33 |
| 5X | −17 | −14 | −13 | −13 | −11 | −13.4 |
| 6X | −12 | −10 | −10 | −9 | −7 | −9.65 |
| 7X ∗ | −5 | −4 | −4 | −3.5 | −2 | −3.85 |
| 1Y ∗ | 3 | 4 | 4 | 3.5 | 2 | 4.09 |
| 2Y | 10 | 13 | 13 | 14 | 17 | 13.21 |
| 3Y | 18 | 21 | 22 | 23 | 29 | 22.25 |
| 4Y | 24 | 27 | 29 | 30 | 35 | 28.79 |
| 5Y | 27 | 34 | 35.5 | 37 | 44 | 34.89 |
| 6Y | 35 | 38 | 40 | 42 | 50 | 40.25 |
| 7Y | 37 | 40 | 42 | 44 | 52 | 42.32 |
| Large | Medium | Small | Side | |
|---|---|---|---|---|
| Mandible | ||||
| 1X | −20 | −19 | −18 | L |
| 2X | −17 | −16 | −15 | L |
| 3X | −15.25 | −14.25 | −13.25 | L |
| 4X | −14 | −13 | −12 | L |
| 5X | −11 | −10 | −9 | L |
| 6X | −8 | −7 | −6 | L |
| 7X | −3 | −2 | −1 | L |
| 1Y | −5.5 | −4.5 | −3.5 | L |
| 2Y | −15 | −14 | −13 | L |
| 3Y | −24 | −23 | −22 | L |
| 4Y | −30 | −29 | −28 | L |
| 5Y | −36 | −35 | −34 | L |
| 6Y | −39 | −38 | −37 | L |
| 7Y | −40 | −39 | −38 | L |
| 1X | 20 | 19 | 18 | R |
| 2X | 17 | 16 | 15 | R |
| 3X | 15.25 | 14.25 | 13.25 | R |
| 4X | 14 | 13 | 12 | R |
| 5X | 11 | 10 | 9 | R |
| 6X | 8 | 7 | 6 | R |
| 7X | 3 | 2 | 1 | R |
| 1Y | −5.5 | −4.5 | −3.5 | R |
| 2Y | −15 | −14 | −13 | R |
| 3Y | −24 | −23 | −22 | R |
| 4Y | −30 | −29 | −28 | R |
| 5Y | −36 | −35 | −34 | R |
| 6Y | −39 | −38 | −37 | R |
| 7Y | −40 | −39 | −38 | R |
| Maxilla | ||||
| 1X | −22 | −21 | −20 | L |
| 2X | −19 | −18 | −17 | L |
| 3X | −17 | −16 | −15 | L |
| 4X | −15 | −14 | −13 | L |
| 5X | −14 | −13 | −12 | L |
| 6X | −11 | −10 | −9 | L |
| 7X | −5 | −4 | −3 | L |
| 1Y | 5 | 4 | 3 | L |
| 2Y | 14 | 13 | 12 | L |
| 3Y | 23 | 22 | 21 | L |
| 4Y | 30 | 29 | 28 | L |
| 5Y | 36.5 | 35.5 | 34.5 | L |
| 6Y | 41 | 40 | 39 | L |
| 7Y | 43 | 42 | 41 | L |
| 1X | 22 | 21 | 20 | R |
| 2X | 19 | 18 | 17 | R |
| 3X | 17 | 16 | 15 | R |
| 4X | 15 | 14 | 13 | R |
| 5X | 14 | 13 | 12 | R |
| 6X | 11 | 10 | 9 | R |
| 7X | 5 | 4 | 3 | R |
| 1Y | 5 | 4 | 3 | R |
| 2Y | 14 | 13 | 12 | R |
| 3Y | 23 | 22 | 21 | R |
| 4Y | 30 | 29 | 28 | R |
| 5Y | 36.5 | 35.5 | 34.5 | R |
| 6Y | 41 | 40 | 39 | R |
| 7Y | 43 | 42 | 41 | R |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


