Material and methods

The institutional review board of Seoul National University School of Dentistry for the protection of human subjects reviewed and approved the research protocol (number S-D 20140018).

The subjects consisted of 204 patients (103 women and 101 men with an average age of 24 years) who had undergone surgical correction of a severe Class III malocclusion. All subjects were of Korean ethnicity. All patients received mandibular setback surgery, and 133 patients had LeFort I maxillary osteotomy. Genioplasty was performed for 81 patients. Table I provides further details of the patients with regard to ages at surgery and some cephalometric and occlusal characteristics. All patients had ceased growing and were healthy, without cleft lip and palate, injury, or craniofacial syndrome.

Preoperative lateral cephalograms were taken close to the time of surgical correction. The data were collected prospectively with the postoperative radiographs taken at least 4 months (average, 9.1 months) after surgery to allow any residual soft-tissue swelling to resolve.

Thirty-nine skeletal landmarks and 32 soft-tissue landmarks from glabella to the terminal point were identified. With its origin at sella, the vertical reference was established perpendicular to the sella-nasion line plus 7°. Using a custom digitizing program via C# programming language (Microsoft, Redmond, Wash), the coordinates of every landmark on each tracing were sequentially computed in relation to the x and y reference system.

The prediction process had 2 stages: building a prediction equation through model fitting, and validation by applying the equation to each subject and calculating test errors. Figure 1 is a flow diagram for establishing the prediction model in this study.

Flow diagram of establishing the prediction model in this study.

Two hundred twenty-six predictor variables and 64 response variables were entered into the prediction equation. The predictor variables included each patient’s age and sex, time after surgery, 1-jaw vs 2-jaw surgery, conjunctive genioplasty, amount of asymmetry, 39 presurgical skeletal landmarks, 32 soft-tissue landmarks before surgery, and 78 (39 × 2) variables measuring the surgical skeletal repositioning in both the anteroposterior and vertical directions. The 64 (32 × 2) response variables were set as the soft-tissue position after surgery in the 32 soft-tissue landmarks in both the x-axis and the y-axis.

The training data set was numerically treated via centering and normalization. The centering made the following computations numerically well conditioned. The normalization gave each variable equal influence in the initial stage of the data analysis.

Two multivariate methods of constructing prediction equations were developed using the conventional OLS and the PLS methods.

First, the conventional OLS method covers from a simple ratio statistics or correlation analysis to a more complex multiple linear regression. In this study, the multivariate multiple linear regression with forward variable selection was used. The model was selected with the Akaike information criterion; the lower this criterion, the better the model will be.

Second, the PLS method is a multivariate regression with latent variables (also called components). This latent variable method was used to focus the information of a large data set into a few underlying components or factors, leaving most of the measurement noise behind as residuals. Although some mathematical details would have been needed, we emphasized the methods and results rather than their theoretical background. With regard to more detailed mathematical properties and interpretations for the PLS method, please refer to the studies of Hastie et al and Wehrens.

In the training data set, the absolute error values after fitting the prediction equation (also called training error) were measured.

After constructing the prediction equation in the training data set, the validation was performed in the test data set (also called the validation data set), and test errors (also called validation errors) were calculated for each subject. We applied the leave-1-out cross-validation technique. The test errors were also used to determine the optimal number of PLS components. From the statistical and clinical viewpoints, the test error is the most important criterion in determining the best prediction model. To restate, the lower the test errors, the better the prediction model becomes.

Plus and minus errors of the prediction could cancel each other out when mean errors are being calculated. Therefore, test errors in the forms of absolute values and root mean square error values of prediction were used as the decision criteria for the predictive performance.

Having chosen the final prediction model, we compared the prediction accuracy between the OLS and PLS methods, and between the 1-jaw and 2-jaw surgery patients.

The free statistics software language R was used. It runs on a wide variety of UNIX platforms, Windows (Microsoft), and MacOS (Apple Inc, Cupertino, Calif). The entire data and complete results without personal patient information will be available upon request to the authors.

Results

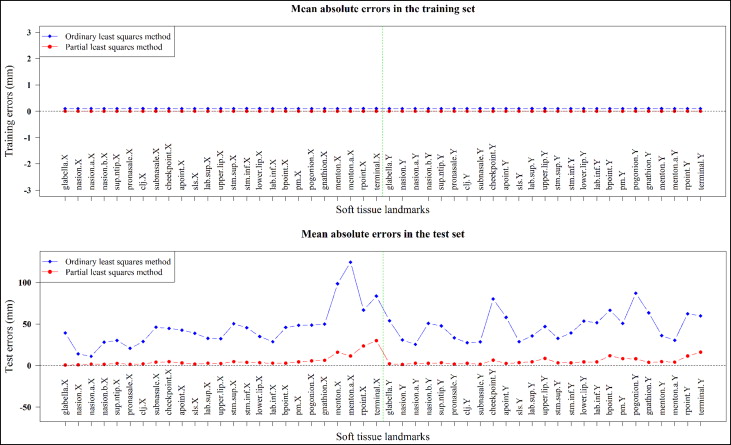
At the stage of building prediction equations, the goodness of fit or the quality of model fitting can be expressed as the extent of training errors. The training errors from both the OLS and PLS methods were negligible or trivial, as shown in Figure 2 (top). However, after applying the prediction equation to each subject in all response variables, the test errors showed significantly lower errors in the PLS method than in the conventional OLS method ( Fig 2 [bottom]).

Training errors ( top ) and test errors ( bottom ) in the mean absolute values showing the fitting quality of the OLS and the PLS predictions. Top , the training errors at the stage of constructing the equation were negligible and close to zero. The training error values were not perfectly the same but almost coincident. To graphically give a little jitter to eliminate ties, the OLS errors ( blue dots ) included artificial additions. Bottom , however, after applying the prediction equation to each subject, the test errors in the form of mean absolute values were calculated, showing considerable differences between the OLS and PLS methods.

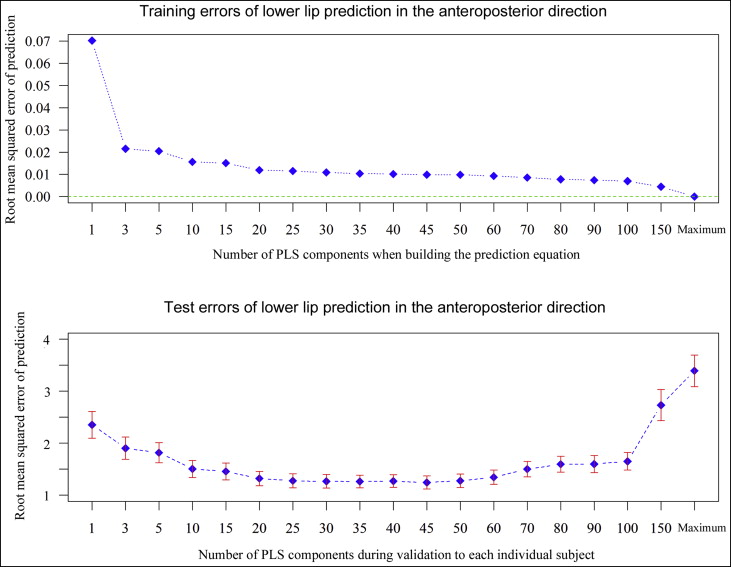
A root mean square error of prediction curve was used to select the best prediction model. Figure 3 shows the root mean square error of prediction curves in both the training and the test data set for a selected landmark. In building prediction equations with the training set, the more components that were included, the smaller the predicton errors obtained. The full prediction model with the entire components had no error in the training set. However, when validating the equation to each subject, there was an optimum number of components to minimize prediction error in the test set ( Fig 3 ). Typically, we chose the smallest model that minimized the expected prediction error. Therefore, the PLS prediction equation with 30 components was selected as the final prediction model.

Root mean square errors of prediction curve in the training data set ( top ) and in the test data set ( bottom ) after validation of the prediction equation to each subject. The increasing number of PLS components decreased the training error ( top ). However, increased complexity of the prediction equation also increased the test error ( bottom ). The PLS prediction equation with 30 components was selected as the final PLS prediction model.

Soft-tissue prediction accuracy was compared between 1-jaw (mandibular setback) and 2-jaw surgery patients; this is given in Table II . Among all 32 soft-tissue landmarks, 12 were chosen to concisely report the results. There was no statistically significant difference in the test errors between the 1-jaw and 2-jaw surgeries.

Table II

Comparison of test errors between 1-jaw (mandibular setback) and 2-jaw surgery patients

Soft-tissue landmark	Anteroposterior error ( x direction, mm)		P value	Vertical error ( y direction, mm)		P value
	1-jaw (n = 71)	2-jaw (n = 133)		1-jaw (n = 71)	2-jaw (n = 133)
Soft-tissue A-point	0.86	0.92	0.517	1.05	1.19	0.265
Superior labial sulcus	0.85	1.03	0.059	1.50	1.40	0.535
Labrale superius	1.02	1.23	0.072	1.38	1.35	0.828
Upper lip	1.07	1.28	0.092	1.37	1.32	0.698
Stomion	1.43	1.54	0.491	0.96	1.00	0.717
Lower lip	1.29	1.26	0.828	1.60	1.48	0.471
Labrale inferius	1.21	1.18	0.857	1.85	1.58	0.196
Soft-tissue B-point	1.14	1.26	0.346	1.93	1.92	0.962
Protuberance menti	1.17	1.23	0.649	1.79	2.05	0.258
Pogonion	1.36	1.33	0.822	2.08	2.45	0.208
Gnathion	1.92	1.74	0.401	1.69	1.58	0.625
Menton	3.96	4.16	0.692	1.61	1.45	0.390

Only gold members can continue reading. Log In or Register to continue

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

Related

Related posts:

1. Pitching speed
2. Etiology of gingival recession
3. Variability of the inclination of anatomic horizontal reference planes of the craniofacial complex in relation to the true horizontal line in orthognathic patients
4. Surgically assisted rapid maxillary expansion: Cone-beam computed tomography evaluation of different surgical techniques and their effects on the maxillary dentoskeletal complex
5. Dimensions of central incisors, canines, and first molars in subjects with Down syndrome measured on cone-beam computed tomographs
6. Correction of facial asymmetry and maxillary canting with corticotomy and 1-jaw orthognathic surgery

Stay updated, free dental videos. Join our Telegram channel

Join