Chapter 10
Basics of Business Finance
The safest way to double your money is to fold it over once and put it in your pocket.
Frank McKinney Hubbard (Kin Hubbard)
compounding
down payment
economic useful lifetime
equipment replacement plan
future value
future value of a present amount
gross lease
interest
IRS useful lifetime
leasehold improvements
leverage
loan amortization
loan conditions
money factor
net lease
operating lease
payment
present value
present value of a future dollar
principal
property lease
residual value
sublease
term of a loan
time value of money
triple net lease
value of an annuity
Business finance looks at how dentists use money in the dental practice to gain or improve profitability. Dentists use it to purchase equipment and materials, hire staff members, and pay costs of the business. Applying finance principles properly maximizes the profit from the practice.
Time Value of Money
A basic premise of finance is that money has a time-associated value, and time has a money-associated value. A dollar in the future will be worth less than a dollar received today, just as paying a dollar in the future is less costly than paying a dollar today. There is a psychological reason for this, given that most people prefer the certainty of having a dollar now to the uncertainty of having a dollar in the future. That future dollar will be worth less because of the likelihood of inflation eating away at its buying power. In addition, a dollar invested wisely will bring a positive return, increasing the value of that present dollar in the future. Time value of money calculations let a person evaluate how much less that future dollar is worth so he or she can make informed financial decisions. This is done by bringing cash flows to a present value for comparison. The higher the assumed interest rate, the more important these calculations become.
These calculations all depend on the idea of compounding. This is the financial process in which a person earns interest on the principal amount, and then he or she earns interest on the interest and the principal. That person then earns interest on an increasing amount over time. The total amount compounds as the interest portion becomes larger and larger.
For example, a person feels that he or she needs $3 million (in today’s money) to retire comfortably in 30 years. If a 3-percent annual inflation is assumed, how much will need to be saved each year to meet the goal? A person agrees to buy a dental practice for $350,000 in 5 years. How much is that in today’s money? The answers to these questions have an obvious, important financial impact.
These numbers can easily be calculated with a financial calculator (e.g., HP 12-C), by using spreadsheet with financial functions (Excel), or by using the tables that included with this chapter. Although these tables do not give the precise results that a banker may have, they are more than adequate for planning purposes. Throughout the chapter, several common examples of using these important techniques are given.
Future Value of a Present Amount
The future value of a present amount is the future amount of an initial deposit when compounded for a given number of periods at a given rate. This calculation is important when planning future expenditures or savings. To compute this amount, the first three of the four values is needed:
| PV | present value, the amount in today’s dollars |
| i | interest rate, the compounding rate for each period |
| n | number of periods, number of compounding periods |
| FV | future value, the amount in future dollars |
Using Table 10.1, find the future value factor (FVF) for the given i and n. Multiply the PV by the FVF to figure out the FV.
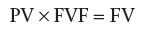
Example Problem 1
A person invests $2,000 in a CD earning 8% interest, compounded annually. What will the CD be worth when it matures in 5 years?
Looking at the table, find the FVF at the intersection of 8% and 5 periods (1.4693). Multiply this FVF by the PV ($2,000) to find the FV $2,938.60.
Example Problem 2
A person needs $3 million (in today’s money) to retire comfortably in 30 years. If a 3% annual inflation is assumed, how much will be needed in today’s dollars to meet the goal?
Looking at the table, find the FVF at the intersection of 3% and 30 periods (2.4273). Multiply this FVF by the PV ($3,000,000) to find the FV $7,281900.
Example Problem 3
A person wants to start a college fund for a newborn daughter. He or she believes that $120,000 ($30,000 per year times 4 years) in today’s dollars is needed, and this money in will be needed in 20 years. Assuming a 3% annual inflation, how much will be needed in today’s dollars for the daughter’s college fund?
Looking at the table, find the FVF at the intersection of 3% and 20 periods (1.8061). Multiply this FVF by the PV ($120,000) to find the FV $216,732.
Table 10.1 Future Value of a Single Present Amount
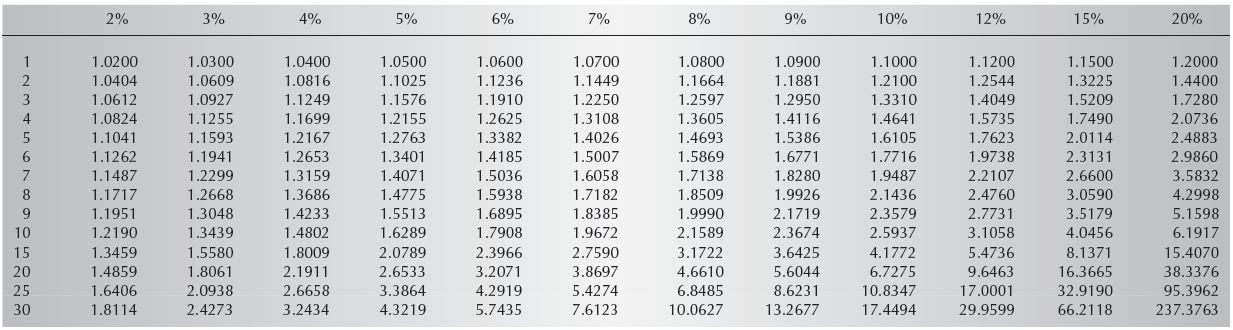
Table 10.2 Present Value of a Future Amount
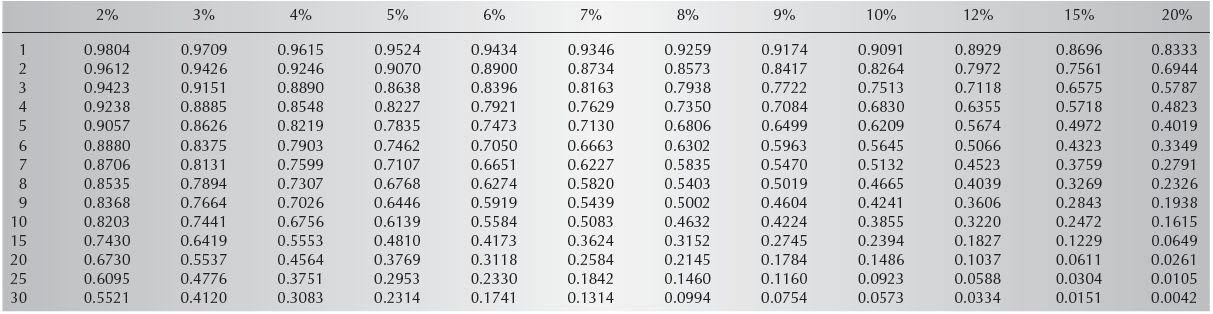
Present Value of a Future Dollar
The present value of a future amount is how much must be deposited today to have a given amount in the future, when compounded for a given number of periods at a given rate. This calculation is not used as much as the other calculations, but it is still important when planning future expenditures. To compute this amount, the first three of the four values are needed:
| FV | future value, the amount in future dollars |
| i | interest rate, the compounding rate for each period |
| n | number of periods, number of compounding periods |
| PV | present value, the amount in today’s dollars |
Using Table 10.2, find the present value factor for the given interest and number of periods. Multiply the FV by the PVF to figure out the PV.
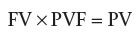
Example Problem 1
A person wants to save $30,000 in 5 years for a down payment on a vacation home. How much should be deposited today to have $30,000 in 5 years? It is believed that 8% can be earned after taxes on the investment.
Looking at the table, find the PVF at the intersection of 8% and 5 periods (0.6806). Multiply this PVF by the FV ($30,000) to find the PV ($20,418). That is to say, if a person deposits $20,418 in an account and earns 8%, after 5 years it will be worth $30,000.
Value of an Annuity
An annuity is a series of regular, periodic payments. When a person buys a car and sets up a loan, it is repaid as an annuity. If a savings plan is established in which a certain amount is set aside each month, an annuity has been established. Because an annuity compounds (i.e., earns interest on the interest earned) a table is needed to determine how much the annuity earns, or costs. Two annuity tables will be used. One determines how much a regular savings plan will be worth in the future. The other determines how much the payment on a loan will be.
Determining Payments
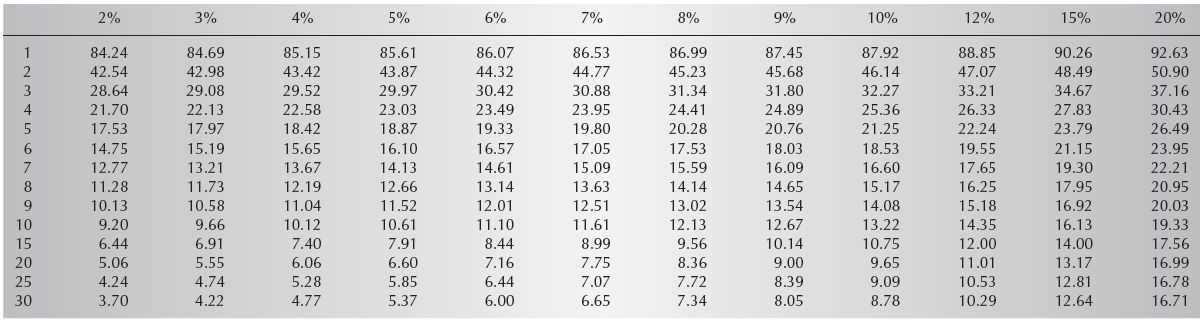
When a person repays loans as an annuity, the loans are usually compounded monthly. Table 10.3 determines a monthly payment based on compounding the interest monthly. If the interest is 12 percent per year compounded monthly, the actual interest rate is 12.68 percent (1 percent compounded monthly). This amount will be more than an annual compounding amount, but it is more accurate. (The tables have this conversion built into them.)
To compute the payment amount, the first three of the four values is needed:
| PV | present value, the amount of the loan principal |
| i | interest rate, the annual interest rate charged on the loan |
| n | number of years, number of years you will pay on the loan |
| PMT | payment, amount of the periodic payment |
Use the table to determine the annuity monthly payment (AMP) factor for the loan’s interest annual interest rate and term (number of years). Multiply the resulting AMP by the number of thousands of dollars of loan principal. Remember this is a monthly payment per $1,000 borrowed. Be sure to multiply by 12 for an annual amount.
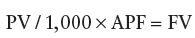
Example Problem 1
A person is buying a new car. The price of the car is $28,000. A $2,000 down payment is made, and the loan is at 9% for 4 years. What is the monthly payment?
Looking at the table, find the AMP at the intersection of 9% and 4 years ($24.89). Multiply this AMP by the number of thousands borrowed (Present Value/1000 = 26) to find the monthly payment amount $647.14 ($7,766 per year).
Example Problem 2
A person is buying a dental practice. The price of the practice $350,000. The entire amount will be financed. The loan is fixed at 10% for 7 years. What is the monthly payment for the practice?
Looking at the table, find the AMP at the intersection of 10% and 7 years ($16.60). Multiply this AMP by the number of thousands borrowed (Present Value/1000 = 350) to find the monthly payment amount $5,810 ($69,720 per year).
Table 10.3 Annuity Monthly Payment Factor
Determining Savings
When a regular savings plan is established, an annuity is essentially being set up. A series of regular payments is made into an account. That account earns interest on the money deposited each period and earns interest on interest earned in the account.
To compute the payment amount, the first three of the four values is needed:
| i | interest rate, the annual interest rate earned on the annuity |
| n | number of years, number of years you will pay into the annuity |
| PMT | payment, amount of the annual payment into the annuity |
| FV | future value, the future amount the annuity will be worth |
Use Table 10.4 to determine the future value annuity (FVA) factor for the annuity’s annual interest rate and term (number of years). Multiply the resulting FVA by the amount of the regular annual payment (in dollars).
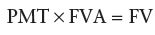
Example Problem 1
A person is saving for a down payment on a vacation home. The home will be purchased in 5 years and can save $1000 per month. It is believed that 8% can be earned in the market (after taxes) on the investment. How much will the person have for a down payment in 5 years?
Looking at the table, find the FVA at the intersection of 8 percent and 5 years (5.867). Multiply this FVA by the annual payment amount ($12,000) to find the value of the annuity at the end of the time ($70,404).
Example Problem 2
A person is saving for retirement. He or she can put $15,000 per year into a tax-deferred retirement account, and he or she estimates earning 12% in the market on the investment. How much will have been accumulated in 30 years?
Looking at the table, find the FVA at the intersection of 12% and 30 years (241.333). Multiply this FVA by the annual payment amount ($15,000) to find the value of the annuity at the end of the time ($3,619,995).
Example Problem 3
A person previously decided that he or she needed $216,732 in 20 years for a newborn daughter’s college fund. If this person believes that 9% (after taxes) can be reasonably earned in the market, how much will need to be saved each year to fund the daughter’s college savings fully?
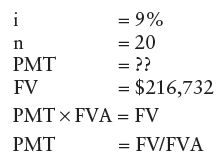
This problem is different in that the future value is known and the payment must be solved for. Looking at the table, find the FVA at the intersection of 9% and 20 years (51.161). Divide the FV ($216,732) by the FVA to figure out the annual savings needed ($4,236) to fund the plan fully.
Capital Budgeting
Capital assets are things that the practice owns that last for several to many years. Examples include dental chairs, computers, curing lights, and furniture. These long-term assets are usually purchased with a loan that last for a long time as well. In fact, most corporate finance officers try to match the term of the loan with the approximate expected lifetime of the asset. A person does not want to extend the term of the loan for a longer period than the useful lifetime. (No one wants to still be paying for a piece of equipment after it has been disposed of.) Capital assets are usually large, expensive pieces of equipment. The decisions about financing these assets carry a large price tag. So planning for the purchase of these assets becomes an important managerial function.
There are several reasons a person might make capital purchases in a dental practice. When buy an existing practice, the person buys the assets of the practice. These may be hard assets (such as dental equipment) and soft assets, such as goodwill and ongoing concern value. The equipment will need to be replaced in a practice periodically as older equipment wears out. A facility might need to be modernized as newer equipment and technology becomes available. An existing facility might need to be expanded. Each of these should be done with a definite plan and timetable for paying for them.
Asset Types
Supplies are things that the practice buys and uses up quickly, usually in less than a year. Assets are things the practice buys that last for more than a year (often many years). These assets are usually broken into soft and hard assets and are then further categorized by their expected useful lifetime (Table 10.5). Two types of “useful lifetimes” are used. The IRS declares a useful lifetime for tax purposes. This determination states how many years must be used in determining the tax depreciation for the asset. Economists are interested in establishing an “economic useful lifetime,” which is an estimate of how long the asset is expected to serve its function for the business before it will need to be replaced. So although the IRS states a 7-year useful lifetime for a dental chair (meaning the chair can be depreciated in no fewer than 7 years), in fact, a dental chair should last for 15 to 20 years, if it is well cared for and well maintained. Its economic useful lifetime (for practice planning purposes) is probably 20 years.
Table 10.4 Future Value Annuity
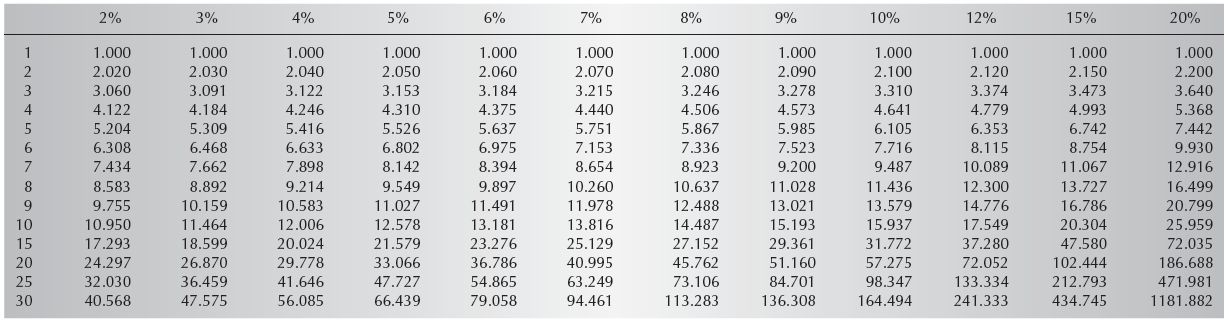
Table 10.5 Types of Assets
| Asset | IRS Useful Lifetime | Economic Useful Lifetime (Estimated) |
| Hard Assets | ||
| Furniture | 7 years | 10 years |
| Dental Equipment | 7 years | 15 years |
| Computers | 5 years | 6 years |
| Buildings | 39 years | 50 yea/> |
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


