Introduction
The purposes of this study were (1) to discover a simple method for computing an average dental form, (2) to evaluate the validity of the new computing method, and (3) to build an average digital dental model based on the resulting average dental form.
Methods
Dental casts of 51 adults were scanned, and 3-dimensional virtual models were reconstructed by using specialized software. Fifty-two anatomic landmarks were plotted on each model to obtain a configuration representing that model. The averaging method was a simplified approach of the generalized partial Procrustes analysis (GPPA); called multiple partial Procrustes analysis (MPPA), it was used to superimpose the 51 sample configurations. For the evaluation method, the GPPA was performed to estimate the population mean form. This mean form was compared with the average forms obtained from the proposed method by using the Procrustes distance as the measure of difference. Construction of the average dental model was based on an average form obtained from the proposed method, and a 3-dimensional dental mesh model was reconstructed.
Results
The average forms from the proposed method showed no significant differences compared with the one from the GPPA. The Procrustes distances were about 0.01 mm, which can safely be considered insignificant.
Conclusions
The proposed averaging method, which is simpler than the traditional GPPA approach, was found to be feasible for computing average dental forms. The average dental model constructed in this study might serve as a guide for treatment planning in orthodontic and prosthodontic dentistry.
The dental arch has long been studied and described by researchers. Many of their efforts were concentrated on describing the arch as a mathematic function. Various methods have been used to define the arch form in this method, including geometric curves, such as a parabola and ellipse to geometric functions, such as catenary curves, polynomials, cubic spline functions, conic sections, the beta function, a combination of polynomial function, parabola, and hyperbolic cosine function, and Fourier analysis. It has been shown by many authors that these mathematic functions can be an accurate planar representation of the natural arch form. However, these curves were expressed only in 2-dimensional (2D) planar space, not in 3-dimensional (3D) space.
Andrews made measurements on patients with excellent occlusions who were both untreated and treated. These measurements were used to fabricate brackets for each tooth and collectively became the concept of preadjusted appliances and straight wires. This became known as the straight-wire appliance (A Company, San Diego, Calif). In his research, the measurements were concentrated on the labial and buccal surfaces of each tooth because preadjusted brackets are placed on those surfaces. However, after Invisalign (Align Technology, Santa Clara, Calif) was introduced, a series of removable polyurethane aligners are used as an esthetic alternative to fixed labial orthodontic appliances. Now, the labial and buccal surfaces are not the only surfaces where great attention should be given. Instead, the 3D positions of cusps and incisal edges have become the critical sites and landmarks for orthodontic treatment planning. In addition, since removable polyurethane aligners wrap around each tooth in the Invisalign technique, the concept of an ideal and normal position for each tooth has become more important.
Although numerous studies have described the dental arch, not enough studies have been conducted 3 dimensionally to compute the average dental arch. Therefore, the aims of this study were to discover a simple method for computing the 3D average dental form, evaluate the validity of that method, and construct a 3D dental model based on the average dental form. Before delving into the specifics, some consensus on the terminology is due. In this study, we adopted the definition of shape as all the geometric information that remains after the effects of translation, size, and rotation are filtered out from an object. Form differs from shape in that it has the size effect intact.
Material and methods
Fifty-one subjects (33 men, 18 women; ages, 23-32 years; mean, 24.7 years) were carefully selected. The following criteria were used: no previous orthodontic treatment, no anterior or lateral crossbite, no pathologic periodontal conditions, no missing teeth (except wisdom teeth), no cast restorations or cuspal coverage, and clinically normal arch shapes with minimal dental crowding or spacing (≤2 mm).
The selected casts were scanned with a 3D scanner (optoTOP-HE; Breckmann, Meersburg, Germany). The scanner has point accuracy of ± 0.005 mm and resolutions of 0.040 mm in the x- and y-axes, and 0.002 mm in the z-axis. Each cast was scanned from 10 or more different views that were combined by a registration method (iterative closest point algorithm) and rendered 3 dimensionally with software (RapidForm XO version 2; INUS Technology, Seoul, South Korea). The virtual 3D models were measured and analyzed with software (RapidForm 2004, version PP2; INUS Technology). For generalized partial Procrustes analysis (GPPA) and various evaluations, a custom-made software program was used.
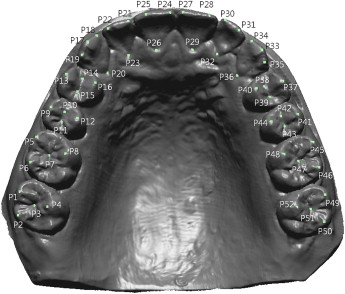
On the surfaces of the virtual dental models, 52 landmarks were spotted and digitized by a well-trained operator (S.-E.N.). Care was taken during this digitizing process to select mainly cusp tips because of their relevance to arch form and their reproducibility ( Fig 1 ).
Some metric measures are mentioned in the ensuing sections. Their definitions are provided here. First, centroid size is the square root of the sum of the squared distances from the centroid of a configuration to each constituent landmark.
where n is the number of landmarks, and |xi−xc|
| x i − x c |
is the distance from the centroid to a landmark.
Procrustes distance is the square root of the sum of the squared distances between the corresponding landmarks of 2 configurations.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


