Review of bone mechanics
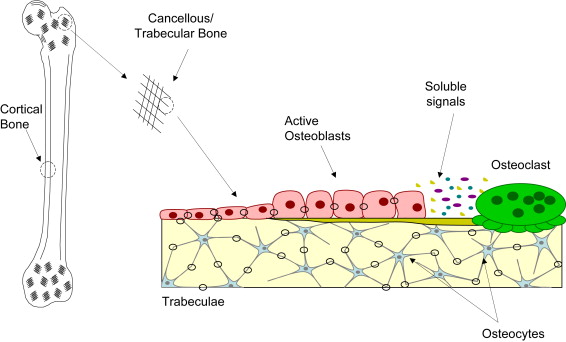
To begin to understand the effects of mechanical forces on bone, such as those that occur during distraction osteogenesis (DO), it is necessary to consider the makeup of the bone and the features that enable it to respond to mechanical loading. Bone is a dynamic organ and, as such, it is in a constant state of change as affected by factors including nutrition, disease, and mechanical environment. Whether these changes alter the quantity or quality of the bone depends upon considerations such as their severity and duration. For practical purposes, bone can be considered a composite material. That is, in addition to water, bone is comprised of organic materials and inorganic matrix. While the organic material, such as collagen, gives bone its resilience and tensile strength, the mineralized matrix gives bone its compressive strength. The mineralized matrix also serves as the structural housing for the osteocytes. The osteocytes are the most abundant bone cells in the body and before becoming encased in their own matrix were bone-forming osteoblasts. These osteocytes reside in lenticular cavities called lacunae. In turn, the lacunae are connected to each other by way of a network of interconnecting channels called canaliculi. While the osteocyte bodies reside in the lacunae, their long, slender processes reside in the canaliculi. Interstitial fluid bathes the lacuno-canalicular network providing for nutrient exchange. This network may also play an important role in transducing mechanical signals. The osteocytes are able to physically link with each other through this porous environment and, many believe, amplify the mechanosensory response at the cellular level such that, among other functions, minimal loading can maintain bone integrity. These bone cells not only link and form networks with each other, but they also maintain contact with the surface-residing osteoblasts. It is hypothesized that the osteocytes act as strain gauges sensing mechanical deformation and communicate this signal to bone-forming osteoblasts that coordinate their activity with bone-resorbing osteoclasts, possibly by way of soluble signaling ( Fig. 1 ). Two important bone types emerge, distinguishable largely by the level of porosity. Cortical (or compact) bone, comprising the hollow shafts of long bones and the thin cortices surrounding trabecular bone, typically has a porosity on the order of 5% to 10%; whereas cancellous (or spongy or trabecular) bone forming the bodies of flat and cuboidal bones typically has a porosity on the order of 75% to 95%. With the interstitial fluid running throughout these porous bone networks, bone is characterized not only by its porous mineral matrix, but also its fluid constituents, giving rise to the distinction that bone is also referred to as a poroelastic material.
When a bone is under mechanical load, its performance is governed by its size, shape, and the material that comprises it. Collectively, these features determine the mechanical properties owing to the fact that they govern the mechanical performance of the bone. Mechanical properties are of two types. Material properties are independent of geometry and describe the substance which makes up the bone. Structural properties are dependent upon geometry and describe the behavior of the structure as a function of the size and shape, or form, it takes. The difference between these concepts can be easily understood if thought of in terms of extremes. For example, in Fig. 2 the steel I-beam (structural building support) and the steel bolt would have identical material properties because they are both made from steel. However because the I-beam is several times larger than the bolt, the structural properties would be quite different. Mechanical properties are determined by mechanical testing and are associated with a particular mode of loading, such as compression or tension.
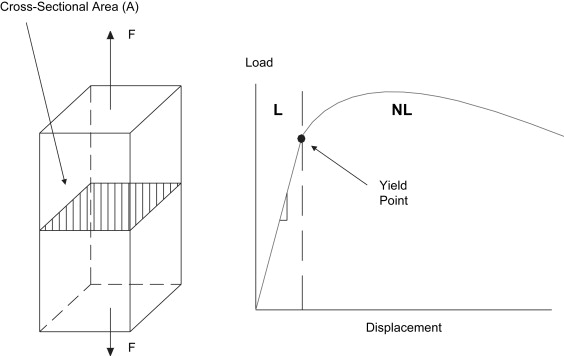
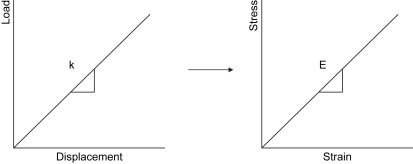
Structural properties are experimentally measured quantities. In the laboratory, one needs only to test a specimen while recording load (load cell) and displacement (displacement sensor) to develop a load versus displacement curve plotting displacement on the horizontal axis and load on the vertical axis. As shown in Fig. 3 , if a bone is tested to failure, the bone will undergo elastic (linear) and plastic (nonlinear) behavior. If we concentrate on only the linear, elastic portion of the curve (to the left of the dashed line), it can be seen that the linear region of the load-displacement curve represents the region in which load is directly proportional to displacement. In this region repeated loading and unloading of the material will not result in permanent deformation and the rate of loading is theoretically not a factor. When the load-displacement curve reaches the point where it is no longer linear (the yield point) permanent deformation will result and the behavior of the material in this region is dependent upon the rate of loading. In the linear region, the slope of the load-displacement curve is called the “stiffness.” Stiffness is an important structural property and is a measure of the compliance of the specimen. That is, the larger the stiffness of a bone, the less likely it is to deflect or deform under a given load.
Material properties are calculated from the data obtained in a load-displacement curve. Stress and strain are constitutive relations and neither can exist independent of the other. Recognizing that a “stress” is simply a measure for a force (load) over a given area and that “strain” is a measure of how much an object changes in length with respect to its initial length (ΔL/L o ), the loads in the force-displacement data divided by the cross-sectional area of the object will generate the stresses. In addition, the incremental displacement data taken with respect to the initial length of the specimen will generate the strains ( Fig. 4 ). A consequence of this simple conversion is that the load-displacement and stress-strain curves will have similar shapes, but different numerical scales.
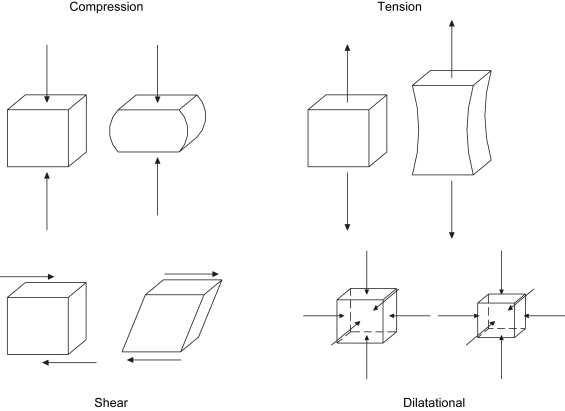
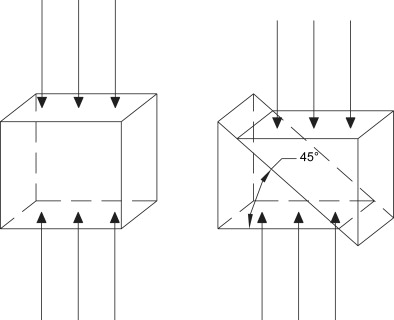
Bone can be subjected to a variety of different loading modes, as demonstrated in Fig. 5 . Here a coupon of bone is shown before and after loading in compression, tension, and shear, respectively. While tension and compression occur along the same axis perpendicular to the loading plane, they have opposite effects on the shape of the material. The shear occurs parallel to the plane and has the effect of moving part of the object relative to another part. Stresses can be more succinctly defined by the affect they have upon an object. Dilatational (hydrostatic) stresses (see Fig. 5 ) result in volume changes whereas deviatoric stresses result in volume distortion. The mechanical loading mode (eg, compression) is not uniform throughout an object. This implies that, if a coupon of bone is subjected to a compressive load, every point within that coupon is not in compression. This may at first seem confusing, but it is an important concept to grasp when studying the mechanical effects of loading bone. Although the mechanics of this are beyond the scope of this writing, the reader needs to be aware that even the simplest loading modes result in complex stress and strain states throughout the bone. As such, compression on a bone coupon can result in regions of the bone experiencing shear. Given that bone, like many objects, is weaker in shear than in compression, a uniform compression load causes the bone to fail in its weakest loading mode, shear. This is illustrated in Fig. 6 . The shear experienced is highest along a plane 45° to the normal and fracture occurs along this plane. This is also the reason that a long bone subjected to pure torsion will experience a spiral fracture along a 45° plane. This behavior is not limited to bone and the reader can easily demonstrate this effect by performing the classic demonstration of applying axial torsion to a piece of blackboard chalk. This demonstrates that by understanding how the various mechanical loading modes affect bone, one can look at a bone fracture to infer the type of loading that caused the failure. This is not limited to the loading mode, but is also reflected in the speed with which the fracture occurred. When bone is fractured slowly, such as occurs during low-energy trauma (falling), the bone has time to absorb energy and a simple fracture results. When bone is fractured quickly, such as occurs during high-energy trauma (a motor vehicle accident), the bone does not have time to absorb the energy and the fracture is comminuted. For obvious reasons, it is desirable that a fracture created by osteotomy/corticotomy in the initial stages of DO is noncomminuted, simple, and stable.
The slope of the stress-strain curve in the linear region is known as the modulus of elasticity or Young’s modulus (E) and is one of three material properties that are needed to completely define a material. For bone, reported values for the Young’s modulus for human cortical bone varies from 17.4 GPa in the longitudinal direction to 3.51 gigaPascal (GPa) in shear and the reported values for the Young’s modulus for cancellous bone varies from 1 to 20 GPa, owing to testing dependence and the increased difficulty in testing trabeculae in comparison to cortical bone.
The second material property known as Poisson’s ratio (ν) is a measure of how elongating or compressing an object will cause necking or bulging, respectively. The Poisson’s ratio is a measure of how loading in the axial direction affects the structure transversely (laterally). With few exceptions, axial tension results in transverse necking while axial compression results in transverse bulging (see Fig. 5 ). For practical purposes the formulation for Poisson’s ratio −[lateral strain/axial strain] is preceded by a negative to account for this inverse relationship and yield a positive numerical value. For bone, a reasonable value of Poisson’s ratio is 0.3.
The third material property, the shear modulus (G) is the slope of the shear stress-shear strain curve in the linear region and is readily determined from a torsion test. Whereas the three material properties completely define a material, the three properties are not independent. That is, determination of any two can enable the calculation of the third, using the relation, G = E/[2(1 + ν)].
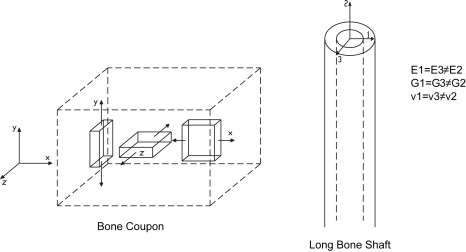
Many materials, such as bone, behave differently depending upon the direction in which they are loaded. When a material property is a function of the loading orientations, the material is termed “anisotropic.” To determine the degree of anisotropy in the laboratory, samples of the material, such as bone, are cut from the block and tested with respect to each of the three orientations ( Fig. 7 ). The load-displacement curve is converted to a stress-strain curve and the elastic modulus is determined. At the same time the loading is applied, the cross-sectional area changes perpendicular to the loading direction are measured to calculate Poisson’s ratio. If the elastic moduli and Poisson’s ratios for each of the three orientations are the same, the material is said to be “isotropic” and the material is completely defined by one E, one G and one ν (three terms). If the values for each of the three orientations are not the same, the material is said to be “orthotropic” and completely defined by three E’s, three G’s and three ν’s (nine terms). Bone is generally considered transversely isotropic (six terms). It is approximated that bone behaves roughly the same in a plane transverse to the long axis of the bone but behaves differently along the axis.