Introduction
Orthodontists depend on perceptions derived from education and clinical experience to judge the optimal forces in patient treatment. The purpose of this study was to survey practicing orthodontists to determine the interarch latex elastic forces they prescribe in different malocclusion scenarios.
Methods
Thirty orthodontists were presented with 4 clinical scenarios on study models, including Class II and Class III malocclusions in edgewise and light wires. These orthodontists described the size and location of the elastics they would use. The forces produced by the prescribed elastics were measured and compared with actual dry forces measured on a testing machine.
Results
The orthodontists’ force recommendations were a mean of 277 ± 89 g and a median of 256 g (range, 132-464 g) for a Class II malocclusion with edgewise wires; a mean of 183 ± 59 g and a median of 177 g (range, 59-284 g) for a Class II malocclusion with light wires; a mean of 290 ± 83 g and a median of 305 g (range, 151-562 g) for a Class III malocclusion with edgewise wires; and a mean of 216 ± 66 g and a median of 209 g (range, 119-344 g) for a Class III malocclusion with light wires. The force levels for light wires were statistically significantly lower than for edgewise wires.
Conclusions
There were considerable variations in the forces selected for all cases. “Expert” recommendations fell within 1 SD of the mean of the orthodontists’ recommendations except for the light-wire Class III scenario. Since latex elastic force decays significantly during a patient’s use, elastics should be selected with initially higher forces than desired.
Force levels in orthodontics are critically important, and orthodontists historically are conscientious in applying only the amount of force needed for healthy tooth movement, whether for archwire engagement in brackets, headgear force, or application of interarch elastics. Force levels, however, might be more in the area of art than of the science of orthodontics, with the art having a strong historical background. In 1910, Angle wrote of the importance of light forces, stating that “when so used it should be very delicate, as described, so that only such gentle forces will be given to the roots of the teeth as to physiologically stimulate the bone-cells. Great force and rapid movement of the apices of the roots of the teeth the writer believes to be unphysiological.” Reitan later found that, with excessive forces, bone and periodontal ligament are compressed and undergo necrosis from ischemia created by blocked blood vessels. The osteoclasts and osteoblasts must then be recruited from healthy adjacent bone before the bone around the tooth can be remodeled. Owman-Moll et al later confirmed the efficacy of light forces, finding that the “undermining resorption” method of tooth movement (heavy force) does not increase the rate at which a tooth will be moved. Although it appears logical that a tooth will move faster if more force is applied, the reality is that the rate of tooth movement is equivalent when comparing undermining resorption tooth movement and physiologic tooth movement. Proffit et al agreed, stating that “heavy continuous orthodontic force can lead to severe root resorption.” Other studies concur that excess forces, including those from interarch elastics, can damage the periodontal ligament, increasing the risk of root resorption. Excess force can also lead to increased pain. Proffit et al suggested that “when areas of periodontal ligament necrosis are avoided. . . pain is also lessened.” It is clear from these findings that the use of optimal force levels is important.
The question then becomes what is the optimal force to accomplish orthodontic treatment goals, yet not be too heavy to cause pain and root resorption? Specific descriptions of optimal force magnitudes for interarch latex elastics are difficult to find in the literature and are found primarily in textbooks. Nanda stated that “an accurate measure of the optimal force eludes determination.” Mulligan acknowledged the difficulty in defining optimal force values when he stated that “an acceptable range of response . . . can vary greatly with each individual.” Graber and Vanarsdall made a similar statement regarding optimal force magnitudes but provided no specific, measurable forces.
Although the literature gives little evidence for optimal force magnitudes, several orthodontists regarded as experts have made recommendations for optimal forces when using latex interarch elastics. Proffit et al listed 2 forces for ideal elastics forces, depending on the size of wire. When using large rectangular wires, he recommended approximately 250 g per side for interarch corrections in his latest textbook edition; this is a reduction from the 300 g in the earlier edition. When using a lighter round wire, Proffit et al recommended only half of the force used for the rectangular wires, or 125 g. Langlade used estimates of root surfaces in conjunction with the suggestion of Ricketts et al of 150 g per square centimeter of resorptive root surface for tooth movement to calculate the force needed to move the maxillary and mandibular dentitions en masse. Based on Langlade’s calculations, an estimated force of 318 g per side would be required. The Alexander discipline provides no force value but advocates the use of .25- in, 6-oz (0.64 cm, 170 g) elastics attached from the maxillary lateral incisor to the mandibular second molar in Class II corrections, and .25-in, 3.5-oz (0.64 cm, 99 g) elastics attached from the maxillary first molar to the mandibular canine.
The recommendations for interarch latex elastics forces are based solely on expert opinions. No studies have compared the experts’ opinions to the actual forces used by practicing orthodontists.
The purpose of this study was to survey practicing orthodontists to determine the interarch latex elastic forces they prescribe in various malocclusion scenarios.
Material and methods
Thirty experienced practicing orthodontists participated in this study, which included all full-time and part-time faculty (n = 15) at the University of Colorado School of Dental Medicine, Department of Orthodontics, and 15 additional orthodontists practicing in the Denver metropolitan area. The University of Colorado did not have an orthodontic training program until 2004, so the participating orthodontists reflect great diversity of training programs and geographic origins, including East Coast, West Coast, and Midwest. Of the 30 orthodontists, 3 did not follow the study protocol and were excluded. The remaining 27 orthodontists were considered representative of the orthodontic community.
A questionnaire and 2 sets of study models were presented to each orthodontist or clinician along with samples of all latex elastics in the study to allow them to feel the amount of force exerted. The orthodontists were allowed to apply the elastics to the models to determine the force. They were given instructions and asked to complete a questionnaire that allowed them to mark the size and location of the latex elastics that they would use to correct the malocclusion in each of the 4 cases. To prevent the confounding variable of intraoral force decay, the participants were told that the patient would wear the elastics for 20 hours per day and change them 3 times per day with the goal of obtaining a Class I molar and canine relationship. The 4 cases differed by the type of malocclusion and the archwire size. Case 1 described a patient in the finishing stages with an edgewise stainless steel archwire (0.018 × 0.025 in [0.45 × 0.63 mm]) and a half-step Class II malocclusion of both the molars and the canines. Case 2 was also a half-step Class II malocclusion but in an earlier stage of treatment with a lighter wire: a round stainless steel archwire (0.018 in [0.45 mm]). Both cases 3 and 4 were described as half-step Class III malocclusions, with an edgewise stainless steel archwire (0.018 × 0.025 in or 0.45 × 0.63 mm) in case 3 and a smaller round stainless steel archwire (0.018 in or 0.45 mm) in case 4.
The models had brackets attached to all teeth with cyanoacrylate (Super Glue; Pacer Technology; Rancho Cucamonga, Calif), and an archwire was in place. All brackets had hooks on the distal aspect of the bracket except for the molar tubes, which had distally curved hooks on the mesial aspect of the tube. Each selected bracket had a hook to allow the orthodontists to place the elastic in the desired position; the brackets were presented to the orthodontists as a generic appliance with only the above definitions and no technique or philosophy connection. The hooks allowed the orthodontists to attach latex elastics to any tooth on the model except for the central incisors. The models were trimmed to American Board of Orthodontics’ specifications and stabilized in the described occlusion for each case by using hot glue on the lingual or palatal surface.
A reference box of latex elastics was included that contained a range of elastics (Rocky Mountain Orthodontics, Denver, Colo). The sizes were (1) 3/8 in (9.5 mm): 2 oz (57 g), 3 oz (85 g), 3.5 oz (99 g), 4.5 oz (128 g), and 5 oz (142 g); (2) 5/16 in (7.9 mm): 2 oz (57 g), 3 oz (85 g), 3.5 oz (99 g), 4.5 oz (128 g), and 5 oz (142 g); (3) 1/4 in (6.4 mm): 2 oz (57 g), 3 oz (85 g), 3.5 oz (99 g), 4.5 oz (128 g), 5 oz (142 g), and 6 oz (170 g); and (4) 3/16 in (4.8 mm): 2 oz (57 g), 3 oz (85 g), 3.5 oz (99 g), 4.5 oz (128 g), and 5 oz (142 g).
Each group of latex elastics was clearly labeled by size and force for easy identification. The orthodontists placed the elastics on the models and marked on the questionnaire to which 2 teeth (1 anterior and 1 posterior) the elastics were attached. They were instructed to use the elastic placement and size that they routinely used in their office and asked not to write any additional comments or add additional sizes of elastics not listed on the questionnaire.
To determine the actual elastic force produced, all 21 latex elastic sizes were tested dry, in vitro, by using a mechanical testing machine (Bionix II; MTS, Eden Prairie, Minn). Five elastics per size were stretched to 60 mm. The elastics were stretched to 60 mm starting from the initial point at which 0.005 N (0.5 g) of force registered on the testing machine. The grams of force exerted by the elastics were measured as they were stretched, producing a force-extension curve for each size of elastic tested. The sample size was determined by referencing a similar study. By using the equation n = (sdv1 2 + sdv2 2 ) × 7.84/(effect size) 2 (sdv = standard deviation), the required sample size for each elastic tested was found to be 2. However, 5 elastics for each size were tested to increase the power of the study. The force extension curves were created from 911 recorded data points, and the data points for each of the 5 tested elastics of the same size and force were averaged at each data point.
To relate the amount of elastic stretch to the actual force produced, the study models were mounted on an articulator in centric occlusion. The articulator was then opened 3 mm at the central incisors from centric occlusion to simulate the clinical rest position. The 3-mm clinical rest position was within the range of 2 to 4 mm found in previous studies. The distance from the anterior attachment to the posterior attachment point listed by the orthodontist was then measured directly from the mounted models. This distance was then used with the appropriate force-extension curve data to determine the amount of force delivered.
The amount of force specified by each orthodontist in each clinical situation was determined, and the means and standard deviations for all orthodontists were calculated. For the expert forces, the values of Proffit et al were taken directly from his textbook of 250 g per side when in large rectangular wire and 125 g per side when in light round wire. Alexander did not give force levels, but recommended a .25-in (6.4 mm), 6-oz (170 g) elastic stretched between the maxillary lateral incisor and the mandibular second molar for Class II corrections and a .25-in (6.4 mm), 3.5-oz (99.2 g) elastic between the mandibular canine and the maxillary first molar for Class III corrections. By using the distance stretched and the force extension curves, the force values on our test models were approximately 380 g (a 40-mm stretch) for a Class II correction and 300 g (a 30-mm stretch) for a Class III correction. Alexander did not have a lighter wire recommendation. Langlade used 318 g per side. Langlade did not differentiate between light and heavy wires but determined the force based on the resorptive root surface, which would be the same for light and heavy wires.
Statistical analysis
The medians, means, and standard deviations were calculated for all outcomes by using SigmaStats Software (Jandel Corp, Corte Madera, Calif). Analysis of variance (ANOVA) was used to determine whether there were differences between the orthodontists’ average force levels in the different case scenarios. The 1-way analyses were followed by a Student-Newman-Keuls a posteriori test. The alpha level was set at P ≤0.05. Comparisons within each treatment group were determined to be more representative if the standard deviations were used to determine the central tendency of all orthodontists. Since the literature recommendations are based on experts’ opinions, rather than actual data, the use of a statistical analysis was deemed inappropriate; hence, comparisons were made with the standard deviations.
Results
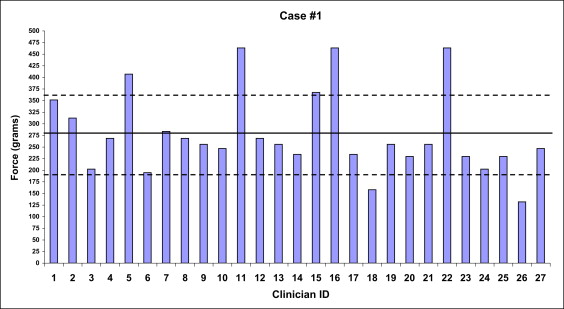
A comparison of the orthodontists’ force values and recommended force levels is presented in the Table and Figures 1-4 . The force-extension graphs for the 21 sizes of latex elastics are shown in Figures 5-8 . For the testing machine results, as the extension increased, the force increased nonlinearly for all elastics; the force started out low with 5-mm extensions and then increased to an extension of 40 to 50 mm, when the slope (the force) began to increase dramatically for most elastics.
| Case | Molar class | Wire size (in) | n | Orthodontists’ selections | Literature | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Median (g) | Mean ± SD (g) | 1-SD range (g) | Minimum/maximum (g) | Statistical difference P ≤0.05 | Proffit (g) | Alexander (g) | Langlade (g) | ||||
| 1 | II | 0.018 × 0.025 | 27 | 256 | 277 ± 89 | 188-366 | 132/464 | a | 250 | 380 | 318 |
| 2 | II | 0.018 | 27 | 177 | 183 ± 59 | 124-242 | 59/284 | b | 125 | NA | 318 |
| 3 | III | 0.018 × 0.025 | 27 | 305 | 290 ± 83 | 207-373 | 151/562 | a | 250 | 300 | 318 |
| 4 | III | 0.018 | 27 | 209 | 216 ± 66 | 150-282 | 119/344 | b | 125 | NA | 318 |