In orthodontics, as well as other fields, the simplest trial would involve a single outcome measure with a comparison of 2 treatments and no subgroup analyses. However, this is not usually the case; often several outcomes are considered, and several subgroup analyses are performed. A recent article recorded subgroup comparisons in articles published by major dental specialty journals and found that over 57% of the included studies had conducted more than 5 multiple comparisons, and 26% of the studies had over 20 multiple comparisons.
What are subgroup analyses and why do we do them? Participants in clinical trials might vary in baseline characteristics such as age, sex, and susceptibility for experiencing the outcome of interest, and their responses to the interventions could depend on their baseline characteristics. Subgroup analyses can be undertaken to identify treatment effects in patient groups that share certain baseline characteristics such as same sex, age, socioeconomic status, oral hygiene level, and cooperation during orthodontic treatment.
For example, let’s assume we are assessing functional appliance vs headgear effectiveness in Class II corrections in adolescent boys and girls. One way to analyze the data would be to perform an overall test between the 2 treatment groups under the assumption that the effects would be the same regardless of sex. However, it could be argued that the response might be different between boys and girls; therefore, those 2 subgroups should be analyzed separately. It is logical to be interested in exploring intervention effects in particular subgroups. However, some potential problems with this approach should be considered.
Problems with subgroup analyses
- 1.
In previous articles, I discussed in some detail sample-size calculations, and readers can refer to them to review the concepts. Sample-size calculations are usually based on assumptions of the analysis of the main outcome and not on subgroup analyses; therefore, subgroup analyses have low power, since they include a portion of the required sample. If there is biological evidence or evidence from previous research that the response to treatment between boys and girls might be different, then this should be considered at the design stage, and appropriate sample-size calculations should be performed at that time to account for the subgroup comparisons.
- 2.
Subgroup tests are usually based on small samples and are likely to give results that might have questionable validity. When we are conducting a statistical test and accept a type I error rate, we are accepting some chance of a false-positive result (ie, a statistically significant treatment effect when in reality no effect exists). The Figure displays the probability of a false-positive result as a function of the number of tests at an alpha level of 0.05. This Figure was derived by plotting the results from the following formula:
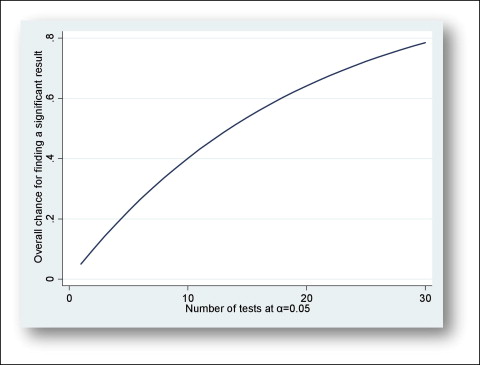
Fig Probability of false positives as a function of the number of comparisons. -
[1 − (1 − a) n], where a is the alpha level, and n is the number of comparisons, assuming that the tests are independent.
-
It is evident that as the number of analyses increases, so does the probability of observing some false-positive results (multiplicity problem).
- 3.
The baseline balance of the treatment group achieved with randomization might be lost between subgroup analyses, and selection bias may arise.
Subgroup comparison tests can be manipulated, and “interesting” results might be overemphasized, thus creating false impressions of treatment effectiveness. The greatest problem with subgroup analyses is that one might find no overall significant effect but then carry out exploratory subgroup analyses that were not specified in advance, until a significant effect is found. It has been said that, if you torture your data long enough, it will confess to anything.
With the problems highlighted above about subgroup analyses, the question then becomes: how should we handle subgroup testing?
One approach would be to lower the threshold for detecting statistically significant results according to the number of intended comparisons. If 10 subgroup comparisons are planned according to the Bonferroni correction, the new threshold will be 0.05/10 = 0.005. In other words, we are making it more difficult to observe a statistically significant result by lowering the threshold from 0.05 to 0.005.
Another approach for handling subgroup analyses is to perform an interaction test. Briefly, we could say that we have an interaction if the effect of an intervention is modified depending on the level of another predictor (we will describe interaction and confounding in more detail in a future article). In the Class II correction example, we might say that we have an interaction if there is a difference in the effect of the functional appliance compared with the headgear between male and female subjects. In other words, the variable sex modifies the effect of the intervention (functional appliance or headgear) depending on its level (male or female). We would not have an interaction if the effect of the intervention was the same across both sexes. Tests for interaction help to guard against spurious findings, and they are the most effective statistical methods to evaluate impacts in subgroup analyses.
Example
We will use a hypothetical example to illustrate the problem of overinterpretation from subgroup analyses. In a trial, we are assessing lingual retainer failures bonded with conventional acid etching vs self-etching primer. Table I shows the results of this trial overall and by age group. Overall, the results are statistically significant. In the younger age group (12-14 years), for a difference of 9.4% between acid etching and self-etching primer, we have a nonsignificant finding ( P = 0.33), whereas in the older age group (15-18 years), for a similar difference between acid etching and self-etching primer (8.0%), we have a statistically significant finding ( P = 0.03). The reason for this aberration is the smaller size of the younger group; this has an influence on the P value, as I explained in a previous article in this column.



