(1)
Department of Neurology Neurosciences Centre, and Clinical Epidemiology Unit, All India Institute of Medical Sciences, New Delhi Delhi, India
Abstract
Tests with Positive/Negative Results: In the dichotomous situation, we usually use two measures of validity (sensitivity and specificity). You can use only likelihood ratio (see later). Validity refers to the degree of correctness of results. ‘Sensitivity’ and ‘specificity’ are measures of validity.
Two-Level (Dichotomous) Test Results
Tests with Positive/Negative Results: In the dichotomous situation, we usually use two measures of validity (sensitivity and specificity). You can use only likelihood ratio (see later). Validity refers to the degree of correctness of results. ‘Sensitivity’ and ‘specificity’ are measures of validity.
Sensitivity is the proportion (or probability) of correct (positive) result in those with disease. This may also be called ‘true positivity’ if positivity is taken to indicate presence of disease or ‘true positive rate’ (but actually this is a proportion, not a rate). This is determined by dividing the number of true positive by the number with disease in the study:
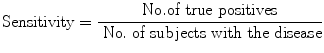
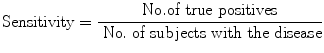
(9.1)
Specificity is the proportion (or probability) of correct (negative) result in those without disease. If the correct result in those without disease is taken as ‘negative’, then specificity may also be called ‘true negativity’ or ‘true negative rate’. This is determined by dividing the number of true negatives by the number without the disease in the study, i.e.
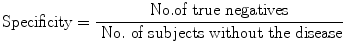
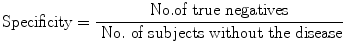
(9.2)
It is desirable to have high sensitivity as well as high specificity. But often, a test is highly sensitive but not highly specific and vice versa. How can we deal with such situations? Well, a highly sensitive test, even if not very specific, can help to ‘rule out’ a disease, if it turns out to be ‘negative’. To remember this, we use the mnemonic ‘SnNOUT’. A highly sensitive (Sn) test, if negative (N), rules OUT the disease. High sensitivity in this context is usually taken as between 0.95 (95 %) and 100 %, depending on the disease under consideration.
Similarly a highly specific test, even if not highly sensitive, can help to ‘rule in’ a disease, if it turns out to be ‘positive’. To remember this, we use the mnemonic ‘SpPIN’. A highly specific (Sp) test, if positive (P), rules IN the disease. High specificity, in this context, is usually taken as 0.95 (95 %) or above.
What do we do if a test is neither 95 % sensitive nor 95 % specific, but 80 % sensitive and 85 % specific? How do we assess its value? How do we respond if a highly sensitive test is positive or a highly specific test is negative? Let us remember that a test is valuable if it significantly changes the probability of a disease (from pretest to posttest). What do we mean by ‘significantly’? ‘Significant’ change here means the change which prompts a decision to treat or do another (probably more invasive) test (from indecisive stage). Now, this depends on what the pretest probability is. If pretest probability is 80 %, then the test with 80 % sensitivity and 85 % specificity, when positive, yields a posttest probability of 95 %. This will nearly always prompt initiation of treatment. Therefore, the test is valuable.
How do we know whether (and how much) a test result will change the pretest probability? For this we need a test parameter called likelihood ratio.
Likelihood Ratio
Likelihood ratio is a link between pretest probabilities and posttest probabilities. It takes you from one to the other (pre to post).
Likelihood ratio (LR) is a ratio of two likelihoods: one in diseased (those with the disease of interest) and the other in non-diseased (non-diseased does not necessarily mean healthy; it means those without the disease of interest). LR tells us how many times more (or less) often a test result is seen among those with the disease as compared to those without the disease. To determine this, we obviously need a ratio which compares likelihood of a test result among those with the disease compared with those without the disease. In other words,
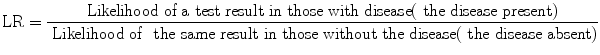
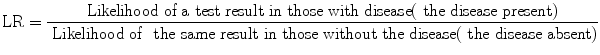
If we know this, it is easy to find the posttest probability either using a nomogram or a formula. The nomogram prepared by Fagan [1] has three vertical lines. You need to select one point corresponding to the pretest probability and the second corresponding to the likelihood ratio of the test result on the appropriate lines of the nomogram. If you join these two lines and extend it to meet the rightmost line of the nomogram, the meeting point gives you the posttest probability of the disease with the given test result. You can also use the following formula to determine posttest probability from pretest probability and likelihood ratio:
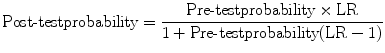
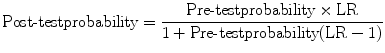
(9.3)
For example, let us consider the study by Guyatt et al. [2] for diagnosis of iron-deficiency anaemia in the elderly. Let us ask how good is serum ferritin level in diagnosis of iron-deficiency anaemia in the elderly. Guyatt et al. included 235 consecutive elderly patients with anaemia in the study. Serum ferritin and bone marrow aspiration results (gold standard) were obtained in all the patients. The results are presented in Table 9.1.
Table 9.1
Results of a study of iron deficiency anaemia: serum ferritin vs bone marrow (gold standard)
|
Bone marrow result
|
||
|---|---|---|
|
Serum ferritin level (μg/L)
|
Iron deficient
|
Not iron deficient
|
|
≤18
|
47
|
2
|
|
>18–45
|
23
|
13
|
|
>45–100
|
7
|
27
|
|
>100
|
8
|
108
|
|
Total
|
85
|
150
|
As you see, serum ferritin results have been grouped into four subgroups. A subgroup is called ‘stratum’ (plural strata). We can say the serum ferritin results are presented in four strata. Now, let us calculate LRs. LR is always for a test result (not for a test). Since there are four strata of test results, we will calculate an LR for each stratum separately (stratum-specific LR). Let us recap the formula for LR:
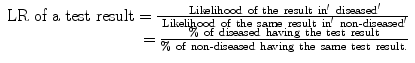
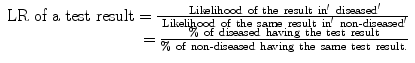
Stratum-specific likelihood ratios (LR) for serum ferritin level:
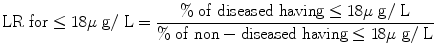
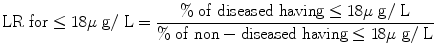
Total no. of ‘disease’ are 85.
No. of ‘diseased’ having ≤18 μg/L = 47.


Total no. of ‘non-diseased’ (not iron deficient) = 150.
No. of ‘non-diseased’ (Not iron deficient) having ≤18 μg/L = 2.
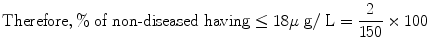
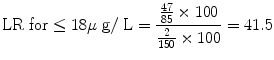
![$$ \text{LR}\ \text{for}/>18-45=\frac{\frac{23}{85}\times 100}{\frac{13}{150}\times 100}=3.1$$
” src=”/wp-content/uploads/1008/A313477_2_En_9_Chapter_Equ000907.gif”></div>
</div>
</div>
<div id=Equ000908 class=Equation>
<div class=EquationContent>
<div class=MediaObject><img alt=]() 45-100=\frac{\frac{7}{85}\times 100}{\frac{27}{150}\times 100}=0.46$$
” src=”/wp-content/uploads/1008/A313477_2_En_9_Chapter_Equ000908.gif”>
45-100=\frac{\frac{7}{85}\times 100}{\frac{27}{150}\times 100}=0.46$$
” src=”/wp-content/uploads/1008/A313477_2_En_9_Chapter_Equ000908.gif”>
![$$ \text{LR}\ \text{for}/>100=\frac{\frac{8}{85}\times 100}{\frac{108}{150}\times 100}=0.13$$
” src=”/wp-content/uploads/1008/A313477_2_En_9_Chapter_Equ000909.gif”></div>
</div>
</div>
</div>
<div class=Para>Now, the question is how will you interpret them.</div>
</div>
<div id=Sec00093 class=]()




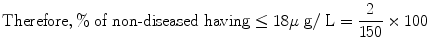
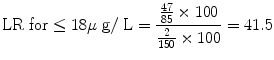
Interpretation of LR: General
What do LRs mean? The LRs indicate by how much a given diagnostic test result will raise or lower the pretest probability of the ‘disease’ under consideration.
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses


