Biological mineral
Publisher Summary
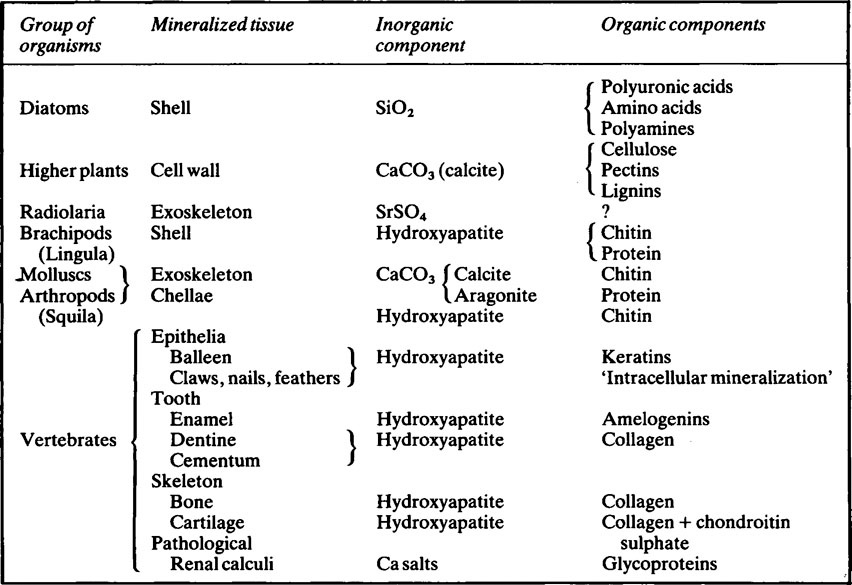
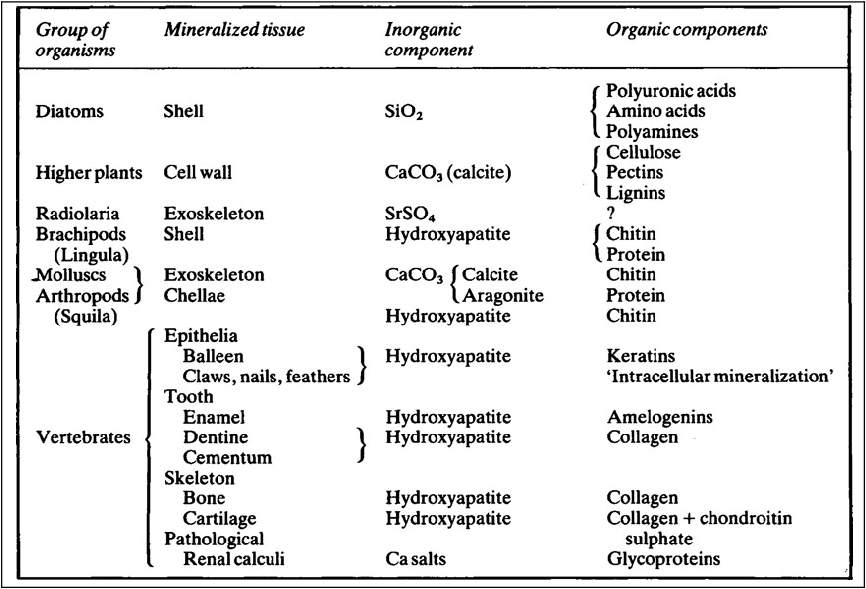
Mineralized tissues consist of an inorganic phase and one or more organic components. Vertebrate mineralized tissues all have a form of calcium phosphate as their main inorganic constituent, but other highly insoluble substances, such as silica, strontium sulfate, and two forms of calcium carbonate, are found in plants and invertebrate animals. A great variety of organic components are present in mineralized tissues, but mainly they are substances of high molecular weight and many of them are polyions. The calcified tissues of vertebrates all have a protein as their main organic constituent, though the type of protein varies. The mineralized tissues of vertebrates are bone, dentine, enamel, and cementum, but these form only a small fraction of those found in the living world. The inorganic components of vertebrate mineralized tissues consist of extremely small crystals, mostly with dimensions of approximately 10–20 × 5 × 5nm. The crystals in dental enamel have a diameter of 40 nm and, although still too small to be clearly resolved by the optical microscope, are considerably larger than those of bone, dentine, and cementum.
Mineralized tissues consist of an inorganic phase and one or more organic components. Some idea of the range of organisms which possess mineralized tissues, together with the types of mineral and organic components they contain is given in Table 28.1. Vertebrate mineralized tissues all have a form of calcium phosphate as their main inorganic constituent, but other highly insoluble substances, such as silica, strontium sulphate and two forms of calcium carbonate, are found in plants and invertebrate animals. Thus, mineralization is not synonymous with calcification.
Biological apatite
The crystalline mineral in bones and teeth is generally regarded as an imperfect calcium hydroxyapatite. Apatite minerals, principally calcium fluorapatite, are both abundant and ubiquitous and are the principal source of phosphate for fertilizers. Their abundance is probably an expression of the very high affinity which calcium and phosphate ions have for each other so that it is perhaps not surprising that, on account of its stability, calcium hydroxyapatite has been selected to play an important part, both structurally and physiologically, in many living things. Ions other than calcium, phosphate and hydroxyl are present in the crystallites in which the atomic ratio of calcium to phosphorus departs considerably from the theoretical value of 1·67 (Table 35.1).
Crystal structure
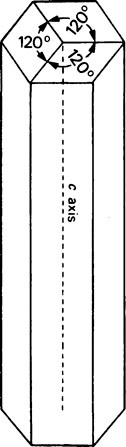
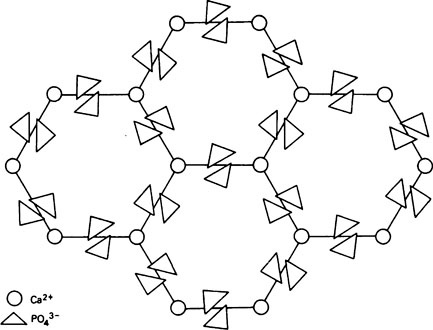
A well-formed crystal of calcium fluorapatite is a prism which can be described as having a principal axis, c, about which there is hexagonal symmetry. Three axes of equal length can be drawn normal to the c axis and at an angle of 120° to each other. These are the a axes (Figure 28.1). The basic structure of the calcium fluorapatite lattice can be likened to the pattern of a honeycomb placed vertically and viewed from above, looking along the c axis. At each of the six corners of each cell of the honeycomb, there is a calcium ion (Figure 28.2). Two phosphate ions lie between each pair of adjacent calcium ions and are displaced somewhat to either side of a line joining the calcium ions. The phosphate ions are tetrahedral in shape with phosphorus at the centre and four oxygen atoms at the apices of the tetrahedron. The projection of the phosphate tetrahedron, when viewed along the c axis, is triangular. The structure envisaged so far is a series of hexagonal cylinders whose points of intersection are formed by calcium ions and whose walls are formed by phosphate ions which are, themselves, in a hexagonal array. Within each hexagonal cylinder or ‘cell’ there are more Ca2+ ions, and also F− ions. The Ca2+ ions are placed at the apices of an equilateral triangle at the centre of which there is a F” ion on the central c axis of the cylinder. The Ca2+ion triangles are stacked on top of each other with the F” ions directly above (or below) each other. Adjacent Ca2+ ion triangles are, however, rotated through 60° with respect to one another. The effect of this rotation is that when the Ca2+ ion triangles are viewed from above, that is, looking along the c axis, they appear as small hexagons (Figure 28.3). When the Ca2+ ion triangles, with their centrally placed F− ions, are incorporated into the larger hexagonal cylinders, the resulting complete calcium fluorapatite structure appears as shown in Figure 28.4. The Ca2+ ions at the corners of the larger hexagons are referred to as column Ca2+ions.
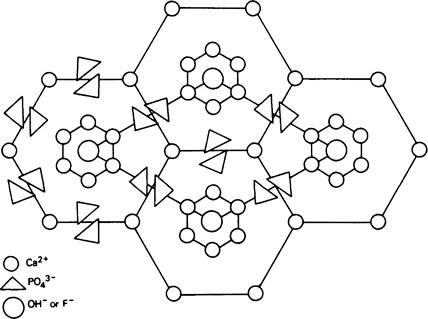
The unit cell
In order to simplify description of the ionic interrelationships in a crystal lattice, an entity known as the unit cell is used. The unit cell is a portion of a crystal which contains the least number of ions necessary to establish all of the ionic relationships which occur in the lattice. Even though a unit cell does not exist by itself, a crystal can be thought of as being built up of hundreds or even thousands of unit cells. The unit cell of calcium fluorapatite contains ten calcium ions, six phosphate ions and two fluoride ions, whilst the unit cell of calcium hydroxyapatite contains two hydroxyl ions instead of the fluoride ions. The ions within a unit cell of calcium fluorapatite and calcium hydroxyapatite can, thus, be written Ca10(PO4)6X2 where X is F− in fluorapatite and OH− in hydroxyapatite. However, since a unit cell has no separate existence, the shorthand expression above is not analogous to the formula for a chemical compound which exists as discrete molecules. Whereas, for example, CH3COOH states the composition of a discrete entity, i.e. a molecule, of undissociated acetic acid, Ca10(PO4)6(OH)2 states the composition of a repeating unit which does not exist on its own. The outline of a unit cell is shown in Figure 28.4 superimposed on the basic honeycomb pattern (Figure 28.2) which is the appearance if the lattice could be viewed along the c axis. The plane in which Figure 28.4 is drawn is at right angles to the c axis and is termed the ab
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses