Clinical Biomechanics in Implant Dentistry
Martha Warren Bidez, Carl E. Misch
The discipline of biomedical engineering, which applies engineering principles to living systems, has unfolded a new era in diagnosis, treatment planning, and rehabilitation in patient care. One aspect of this field, biomechanics, concerns the response of biological tissues to applied loads. Biomechanics uses the tools and methods of applied engineering mechanics to search for structure–function relationships in living materials.1 Advancements in prosthetic, implant, and instrumentation design have been realized because of mechanical design optimization theory and practice.2 This chapter provides fundamental concepts and principles of dental biomechanics as they relate to long-term success of dental implants and restorative procedures.
Loads Applied to Dental Implants
Dental implants are subjected to occlusal loads when placed in function. Such loads may vary dramatically in magnitude, frequency, and duration, depending on the patient’s parafunctional habits. Passive mechanical loads also may be applied to dental implants during the healing stage because of mandibular flexure, contact with the first-stage cover screw, and second-stage permucosal extension.
Perioral forces of the tongue and circumoral musculature may generate low but frequent horizontal loads on implant abutments. These loads may be of greater magnitude with parafunctional oral habits or tongue thrust. Finally, application of nonpassive prostheses to implant bodies may result in mechanical loads applied to the abutment, even in the absence of occlusal loads. So many variables exist in implant treatment that it becomes almost impossible to compare one treatment philosophy with another. However, basic units of mechanics may be used to provide the tools for the consistent description and understanding of such physiologic (and nonphysiologic) loads. Two different approaches may render a similar short-term result; however, a biomechanical approach still can determine which treatment renders more risk over the long term.
Mass, Force, and Weight
Mass, a property of matter, is the degree of gravitational attraction the body of matter experiences. As an example, consider two cubes composed of hydroxyapatite (HA) and commercially pure titanium, respectively. If the two cubes are restrained by identical springs, then each spring will deflect by a certain amount relative to the attraction of gravity for the two cubes. The two spring deflections in this example can be made equal by removing part of the material from the titanium cube. Even though the cubes are of completely different composition and size, they can be made equivalent with respect to their response to the pull of gravity. This innate property of each cube that is related to the amount of matter in physical objects is referred to as mass. The unit of mass in the metric (International System of Units) system is the kilogram (kg); in the English system, it is the pound mass (lbm).3
In 1687, Sir Isaac Newton described a force in what is now referred to as Newton’s laws of motion.3 In his second law, Newton stated that the acceleration of a body is inversely proportional to its mass and directly proportional to the force that caused the acceleration. The familiar relation expresses this law:
< ?xml:namespace prefix = "mml" />
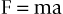
where F is force (newtons [N]), m is mass (kilograms), and a is acceleration (meters per second squared [m/sec2]). In the dental implant literature, force commonly is expressed as kilograms of force. The gravitational constant (a = 9.8 m/sec2) is approximately the same at every location on Earth; therefore, mass (kilograms) is the determining factor in establishing the magnitude of a static load.
Weight is simply a term for the gravitational force acting on an object at a specified location. Weight and force can be expressed by the same units, newtons or pound force (lbf). If a titanium cube is considered as though placed on the moon, then its weight (force caused by gravity) is different from its weight on the Earth. The mass in the cube has not changed, but the acceleration caused by gravity has changed. Recalling Sir Isaac Newton’s work, an apple weighs approximately 1 N (0.225 lbf)4 (Box 5-1).
Forces
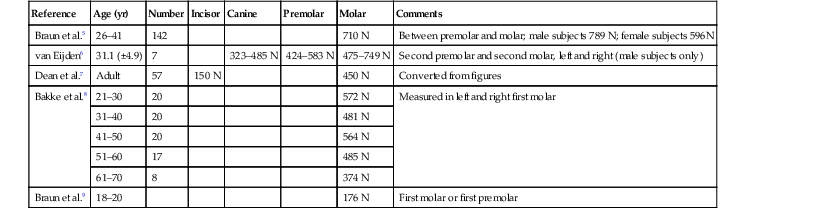
Forces may be described by magnitude, duration, direction, type, and magnification factors. Forces acting on dental implants are referred to as vector quantities; that is, they possess magnitude and direction. Restated, to state simply that “a force of 75 lb exists on the distal abutment” is not sufficient. The more correct statement is “a force of 75 lb exists on the distal abutment directed axially along the long axis of the implant body.” The dramatic influence of load direction on implant longevity and bone maintenance is discussed later in this chapter and others. Typical maximum bite force magnitudes exhibited by adults are affected by age, sex, degree of edentulism, bite location, and especially parafunction5–9 (Table 5-1).
TABLE 5-1
Maximum Bite Force
| Reference | Age (yr) | Number | Incisor | Canine | Premolar | Molar | Comments |
| Braun et al.5 | 26–41 | 142 | 710 N | Between premolar and molar; male subjects 789 N; female subjects 596N | |||
| van Eijden6 | 31.1 (±4.9) | 7 | 323–485 N | 424–583 N | 475–749 N | Second premolar and second molar, left and right (male subjects only) | |
| Dean et al.7 | Adult | 57 | 150 N | 450 N | Converted from figures | ||
| Bakke et al.8 | 21–30 | 20 | 572 N | Measured in left and right first molar | |||
| 31–40 | 20 | 481 N | |||||
| 41–50 | 20 | 564 N | |||||
| 51–60 | 17 | 485 N | |||||
| 61–70 | 8 | 374 N | |||||
| Braun et al.9 | 18–20 | 176 N | First molar or first premolar |
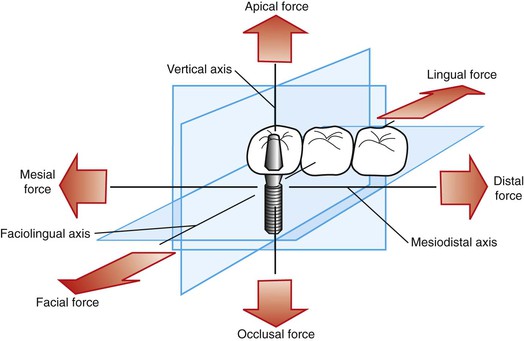
A force applied to a dental implant rarely is directed absolutely longitudinally along a single axis. In fact, three dominant clinical loading axes exist in implant dentistry: (1) mesiodistal, (2) faciolingual, and (3) occlusoapical (Figure 5-1). A single occlusal contact most commonly results in a three-dimensional occlusal force. Importantly, this three-dimensional force may be described in terms of its component parts (fractions) of the total force that are directed along the other axes. For example, if an occlusal scheme on an implant restoration is used that results in a large magnitude of force component directed along the faciolingual axis (lateral loading), then the implant is at extreme risk for fatigue failure (described later in this chapter). The process by which three-dimensional forces are broken down into their component parts is referred to as vector resolution and may be used routinely in clinical practice for enhanced implant longevity.
Components of Forces (Vector Resolution)
Occlusion serves as the primary determinant in establishing load direction. The position of occlusal contacts on the prosthesis directly influences the type of force components distributed throughout the implant system.
The dentist should visualize each occlusal contact on an implant restoration in its component parts. Consider the example of a restored dental implant subjected to a premature contact during occlusion. When the contact is broken down into its component parts directed along the three clinical loading axes, a large, potentially dangerous lateral component is observed. Occlusal adjustments consistent with implant-protective occlusion to eliminate the premature contact minimize the development of such dangerous load components.
Angled abutments also result in development of dangerous transverse force components under occlusal loads in the direction of the angled abutment. Implants should be placed surgically to provide for mechanical loading down the long axis of the implant body to the maximum extent possible. Angled abutments are used to improve esthetics or the path of insertion of a restoration, not to determine the direction of load.
Three Types of Forces
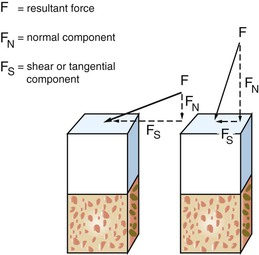
Forces may be described as compressive, tensile, or shear. Compressive forces attempt to push masses toward each other. Tensile forces pull objects apart. Shear forces on implants cause sliding. Whereas compressive forces tend to maintain the integrity of a bone–implant interface, tensile and shear forces tend to distract or disrupt such an interface. Shear forces are most destructive to implants and bone compared with other load modalities. In general, compressive forces are accommodated best by the complete implant–prosthesis system. Cortical bone is strongest in compression and weakest in shear10 (Table 5-2). Additionally, cements and retention screws, implant components, and bone–implant interfaces all accommodate greater compressive forces than tensile or shear. For example, whereas the compressive strength of an average zinc–phosphate dental cement is 83 to 103 MPa (12,000–15,000 psi), the resistance to tension and shear is significantly less (500 psi) (Figure 5-2).
TABLE 5-2
Cortical Bone Strengths in Human Femur Specimens
| Type of Force Applied | Strength (MPa)* | Load Direction/Comments |
| Compressive | 193.0 (13.9) | Longitudinal |
| 173.0 (13.8) | 30 degrees off axis | |
| 133.0 (15.0) | 60 degrees off axis | |
| 133.0 (10.0) | Transverse | |
| Tensile | 133.0 (11.7) | Longitudinal |
| 100.0 (8.6) | 30 degrees off axis | |
| 60.5 (4.8) | 60 degrees off axis | |
| 51.0 (4.4) | Transverse | |
| Shear | 68.0 (3.7) | Torsion |

* Standard deviations are listed in parentheses.
Data from Reilly DT, Burstein AH: The elastic and ultimate properties of compact bone tissue, J Biomech 8:393, 1975.
The implant body design transmits the occlusal load to the bone. Threaded or finned dental implants impart a combination of all three force types at the interface under the action of a single occlusal load. This “conversion” of a single force into three different types of forces is controlled completely by the implant geometry. The prevalence of potentially dangerous tensile and shear forces in threaded or finned implants may be controlled optimally through careful engineering design. Cylinder implants in particular are at highest risk for harmful shear loads at the implant–tissue interface under an occlusal load directed along the long axis of the implant body. As a consequence, cylinder implants require a coating to manage the shear stress at the interface through a more uniform bone attachment along the implant length. Bone loss adjacent to cylindrical implants and coating degradation results in a mechanically compromised implant.
Offset loading on single-tooth or multiple-abutment restorations results in moment (bending) loads (described later under Force Delivery and Failure Mechanisms). As a result, an increase in tensile and shear force components is often found. Compressive forces typically should be dominant in implant prosthetic occlusion.
Multiple abutment restorations, particularly with distal cantilevers, produce a remarkably complex load profile in the prosthesis and in the bone–implant interface. These clinical realities underscore the need for optimizing dental implant design to provide the maximum functional surface area to dissipate such forces.
Stress
The manner in which a force is distributed over a surface is referred to as mechanical stress. Thus, the familiar relation defines stress:
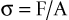
where σ is stress (pounds per square inch; pascals), F is force (newtons; pound force), and A is area (square inches; square meters). The internal stresses that develop in an implant system and surrounding biological tissues under an imposed load may have a significant influence on the long-term longevity of the implants in vivo. As a general rule, a goal of treatment planning should be to minimize and evenly distribute mechanical stress in the implant system and the contiguous bone.
The magnitude of stress depends on two variables: (1) force magnitude and (2) cross-sectional area over which the force is dissipated. It is rare that a dentist can control the force magnitude completely. The magnitude of the force may be decreased by reducing these significant magnifiers of force: cantilever length, offset loads, and crown height. Night guards to decrease nocturnal parafunction; occlusal materials that decrease impact force; and overdentures, rather than fixed prostheses, that can be removed at night are further examples of force reduction strategies. The functional surface area over which the force is distributed, however, is controlled completely through careful treatment planning.
A functional cross-sectional area is defined as that surface that participates significantly in load bearing and stress dissipation. This area may be optimized by (1) increasing the number of implants for a given edentulous site and (2) selecting an implant geometry that has been designed carefully to maximize functional cross-sectional area. An increase in functional surface area serves to decrease the magnitude of mechanical stress imposed on the prosthesis, implant, and biological tissues.
Stress components are described as normal (perpendicular to the surface and given the symbol σ) and shear (parallel to the surface and given the symbol τ). One normal stress and two shear stresses act on each plane (x, y, z); therefore τxy = τyx, τyz = τzy, and τxz = τzx. Thus any three-dimensional element may have its stress state completely described by three normal stress components and three shear components.
The question arises as to what are the peak stresses or maximum stresses that an implant and the surrounding interfacial tissues experience. Peak stresses occur when the stress element is positioned in a particular orientation (or geometric configuration) in which all shear stress components are zero. When an element is in this configuration, the normal stresses are given a particular name, principal stresses, and are indicated as σ1, σ2, and σ3. By convention, maximum principal (σ1) stresses represent the most positive stresses (typically peak tensile stresses) in an implant or tissue region and minimum principal (σ3) stresses, the most negative stresses (typically peak compressive stresses). Sigma 2 (σ2) represents a value intermediate between σ1 and σ3. Determination of these peak normal stresses in a dental implant system and tissues may give valuable insights regarding sites of potential implant fracture and bone atrophy.
Deformation and Strain
A load applied to a dental implant may induce deformation of the implant and surrounding tissues. Biological tissues may be able to interpret deformation or a manifestation thereof and respond with the initiation of remodeling activity.
The deformation and stiffness characteristics of the materials used in implant dentistry, particularly the implant materials, may influence interfacial tissues, ease of implant manufacture, and clinical longevities. Elongation (deformation) of biomaterials used for surgical dental implants ranges from 0 for aluminum oxide ceramics to up to 55 for annealed 316-L stainless steel11 (Table 5-3). Related to deformation is the concept of strain, a parameter believed to be a key mediator of bone activity.
TABLE 5-3
Mechanical Properties of Selected Surgical Implant Biomaterials
Stay updated, free dental videos. Join our Telegram channel

VIDEdental - Online dental courses