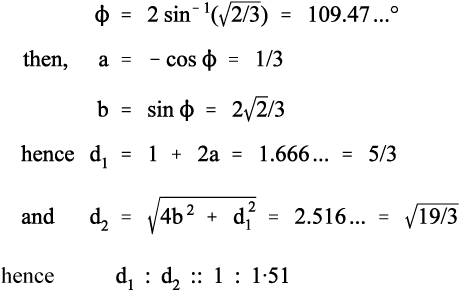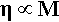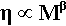Polymers, both synthetic and natural, form the basis of very many dental materials, and these exhibit an equally wide range of properties. This variation in properties is intimately bound up in the structure and behaviour of the molecules. But far from being a mere catalogue of variations, polymer physics and chemistry is explicable, and predictable, in systematic terms of chain structure, side-groups, and cross-linking. This can be taken to the stage of the design and creation of a polymer having particular properties to suit a specific purpose, and indeed this has already been done in many contexts. To understand these polymer properties and design principles in dentistry, or any other applications, it is necessary to deal first with the basics.

§1 Basic Structure

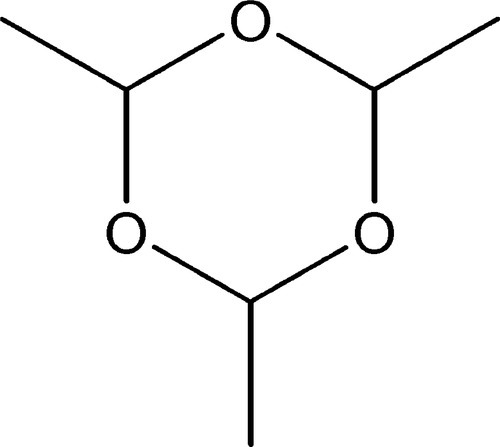
A polymer was originally understood to be the result of polymerization, a process whereby covalent bonding between two or more identical molecules yielded a larger molecule with the same empirical formula, that of the monomer. The usual example of this is the cyclic molecule paraldehyde, (CH₃CHO)₃, formed from acetaldehyde, CH₃CHO (Fig.1.1). However, with the identification of many kinds of giant molecule, the usage of these terms was considerably extended. Thus, an addition polymer molecule is a simple multiple of the monomer, as in paraldehyde, whereas a condensation polymerization proceeds with the elimination of a small molecule, often water, for each monomer molecule reacted. The empirical formula of a condensation polymer therefore differs from that of the monomer; that of an addition polymer is identical to it. As a result of this emphasis on indefinitely large polymers, the smaller molecules, up to say 6 or 10 units, are now preferably called oligomers.

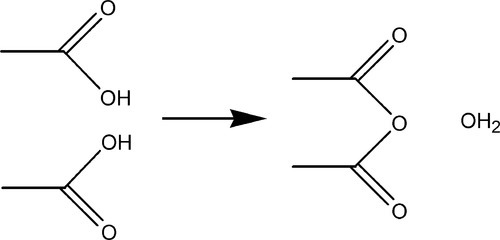
The condensation reaction may be illustrated by the example of acetic anhydride, (CH₃CO)₂O, which is formed from two molecules of acetic acid, CH₃COOH, with the elimination of water (Fig. 1.2). A similar reaction, that of esterification, can also be used (as in the reaction of acetic acid and ethanol to form ethyl acetate), again with the elimination of water. But for polymers to be formed it is necessary that, after each unit has been reacted, the chain continues to have a reactive site for the link to the next unit. Thus, in the case of polyesters, a mixture of diacid and diol may be used, or even an acid-alcohol (hydroxyacid) (see 27§4), so that each end of the chain can grow independently.

In forming both addition and condensation polymers, more than one monomer may be reacting: this is known as copolymerization, i.e. generating a copolymer, with the implication that the sequence is random, but depending on relative concentrations and reactivity. This kind of process leads to a slight difficulty of description, for what is truly a repeating unit in a simple addition polymer, and identifiable exactly in empirical formula with the starting material, does not exist as such in either random copolymers or condensation polymers, and especially not in condensation copolymers. The general term mer can thus be used to indicate a structural unit in a polymer, without prejudice to chemical formula or indeed to its uniqueness in the structure, as long as it is referable as being derived directly from one or other of the starting compounds. A block copolymer, in which alternating sequences of identical mers of one kind or another occur, can also be made for special purposes, a kind of structure further requiring care in description.

Polymeric materials are frequently characterized as being simply long chains of mers, but other structures are possible, indeed common. By introducing reactants with a higher number of functional groups or because of side reactions, branches may be created in the chains, and tree-like molecules or random three-dimensional networks may be made. In biological systems in particular, regular sheets and networks may be found. A number of these larger systems are of relevance to dentistry, and will be dealt with later in the appropriate sections.

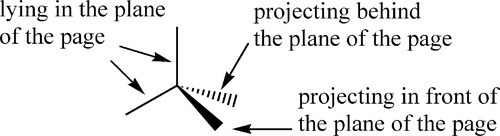
Single σ-bonds between atoms permit the relative rotation of those atoms. Thus, a methyl group CH₃-may rotate with respect to the rest of the molecule to which it is attached. In addition, where two bonds to the same atom have an angle between them which is not 180°, such as the tetrahedral angle of the sp³-hybridized atomic orbitals of carbon, such a rotation changes the relative position in space of the atoms and groups either side of that rotating bond. In larger, more complex molecules where several such rotatable, angled links exist, the molecule may adopt a wide range of shapes or layouts in space. That is to say, it may exhibit various conformations. Notice that interconversion between conformations depends only on bond rotation. There is then, in principle, a simple path between any two conformations without breaking any bonds (assuming no other form of steric hindrance) simply by rotation about one or more bonds.

•2.2 Configuration

When an sp³-hybridized carbon atom has four different substituent groups attached to it, there are just two distinct ways of doing this, which are the mirror image of each other (Fig. 2.1). The central atoms are then said to be asymmetric. The two forms cannot be interconverted at ordinary temperatures by mere rotation of atoms or groups, just as left-and right-hand gloves cannot be superimposed by mere rotation. Interconversion of the two forms requires at least one bond to be broken and reformed in a new position. This situation gives rise to stereoisomerism: two compounds of identical composition and bonding, and therefore structure, are distinguishable by their chirality or handedness. They are said to be stereoisomers or configurational isomers.

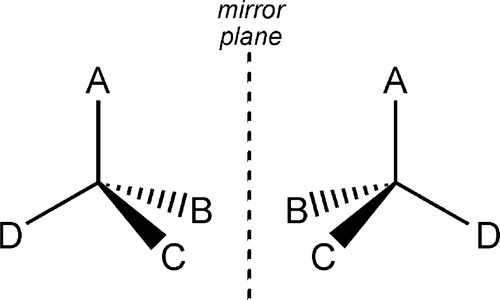
When the monomer has four distinguishable substituents on a carbon atom that will form part of the backbone chain of a polymer, or such asymmetric carbon atoms arise as a result of the polymerization reaction itself, as occurs in poly(methyl methacrylate) (Chap. 5), several possibilities arise for the configuration of the side chains or substituents of that polymer. Hence, polymers with asymmetric carbons are distinguishable by configuration, and are permanently locked into their particular condition, allowing discrimination between the various kinds.

To assist in the interpretation of three-dimensionalmolecular structures, there are various conventions for drawing the stereochemistry of molecular bonds. This isone such:

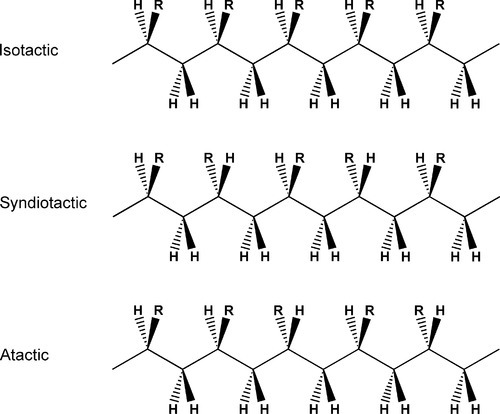
•2.3 Tacticity

While conformation relates to internal movements of molecules, and configuration the way in which a chain is built at any asymmetric carbon, tacticity refers to the ordering of the configuration sequence of a polymer. Thus, if the relative positions of the substituents are always the same, from asymmetric centre to asymmetric centre, along the length of the chain, the polymer is said to be isotactic (Fig. 2.2), whereas an alternating configuration is called syndiotactic. The occurrence of these two arrangements commonly depends on complex steric constraints and they require specialized reaction conditions and methods to be realized. However, for many systems, such as with methyl methacrylate as monomer, no such conditions apply, and the polymer produced is atactic: the substituents are randomly arranged – there is no regularity along the chain. This condition of atacticity has important consequences for the structure of the solid. Because the former two regular types have a repeating structure, not just chemically but also in configuration, they can readily be formed into regular arrays, given that this will require some rotation about successive chain bonds to achieve the correct orientation at each carbon atom. Such polymers therefore can often crystallize quite readily, whereas atactic polymers simply can not crystallize. They are amorphous, resulting in materials which are less brittle than their crystalline counterparts. Crystallinity in polymers is explored further below (§4).

Polymer chains tend to lend the property of plasticity to the material (and hence the common term for manufactured polymers is ‘plastic’) because the chains – or parts of those chains – can be rearranged readily from the usual random coils (Fig. 2.3) to extended chains under moderate forces (Fig. 2.4). It should be noted that this kind of rearrangement for chain extension¹ does in fact depend on rotation occurring at each bond in the chain. It is the relative ease, or even the feasibility, of this rotation that is a highly-significant factor controlling both the physical and the mechanical properties of the bulk polymer. We proceed to examine the energy changes for changes of conformation by rotation, and then the geometrical implications.

•2.4 Ethane

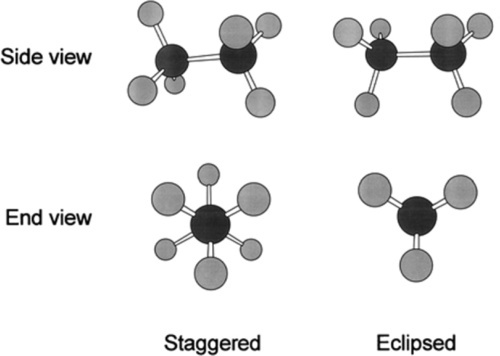
If we consider an ethane molecule, C₂H₆, it can be seen that because of the rotation that can occur at the carbon-carbon σ-bond, the two methyl groups can adopt any relative rotational position with respect to each other. Two of these positions are particular distinct: these are labelled staggered and eclipsed (Fig. 2.5), depending on whether the hydrogen atoms are superimposed or not when viewed along the C-C bond axis, ‘end on’.

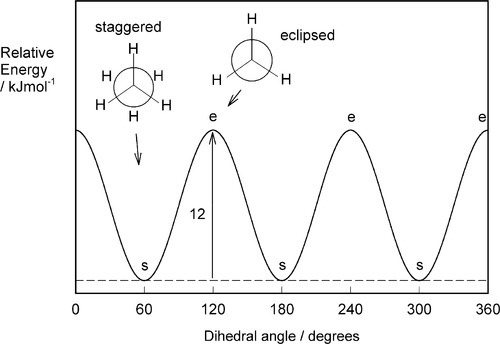
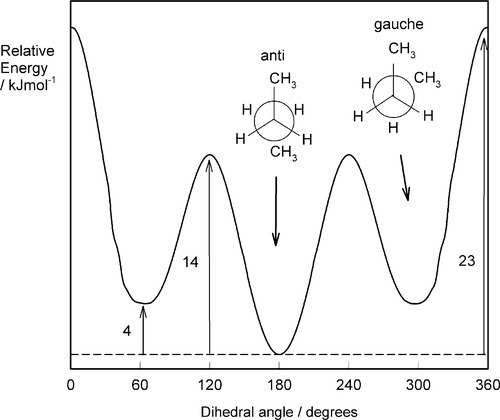
These two positions correspond to the minima and maxima respectively in the plot of energy versus dihedral (rotational) angle (Fig. 2.6). Energy is required to rotate the one methyl group with respect to the other because of the small but important mutual steric interference of the hydrogen atoms. The energy difference between the two positions is about 12 kJ/mol. Because there are three equivalent positions for each hydrogen, the energy variation is cyclic, with three peaks and three troughs, and each portion of the curve is equivalent to the others (Fig. 2.6). The important point here is that the peaks represent an energy barrier to the free rotation about the central bond, the eclipsed form representing the less favourable (i.e. higher energy) position.^[1] Rotation is therefore an activated process, requiring an activation energy. It follows that it is a temperature-dependent process. We can describe the three ‘detent’ positions of the energy minima as rotational isomers or rotamers, even though in this case they are not distinguishable.

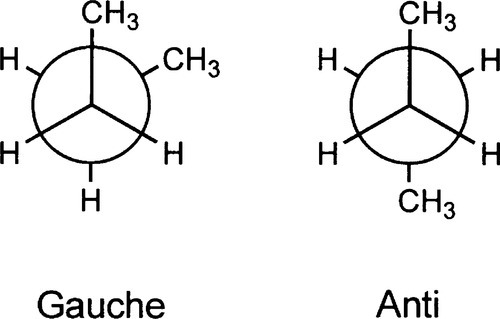
•2.5 Butane

To continue the building of the model, we may take a slightly longer carbon chain, that of n-butane: CH₃-CH₂-CH₂-CH₃. We have now introduced two further position distinctions in respect of the central carbon-carbon bond. That is, the staggered conformation about the central bond can be of two kinds: the terminal methyl groups being either adjacent (gauche) or opposed (anti) to the other methyl group (Fig. 2.7). This leads to a further component of variation in the energy with rotation about the central carbon-carbon bond (Fig. 2.8) because the bulky methyl groups have greater mutual steric interference in what may be termed the fully-eclipsed position, but also because the interference between methyl and hydrogen is greater then hydrogen-hydrogen, making the rotation much more difficult. This general result applies in principle to rotation about any bond in polyethylene, where the methyl groups of butane can be considered as replaced by effectively infinite -CH₂– chains, but the peaks and troughs of the energy curve become slightly more exaggerated.

Extension of the idea can be made to chains with larger substituents than hydrogen. The hindrance is not just steric in the sense of the substituents themselves physically clashing, but the interaction of the bonds themselves is involved, as must be evident from the geometry of ethane. Ball-and-stick models do not adequately represent the true situation, and must not be taken literally. The effect has been considered as the mutual repulsion of the electron clouds of each molecular orbital, although this is a simplistic view, ^[2][3] a more definite stabilization process being involved. The ultimate effect is, nevertheless, extremely important. Polypropylene, for example, which can be ‘derived’ from the polyethylene structure by replacing a hydrogen on every second main chain carbon by a methyl group (i.e. arranged as are the groups R- in Fig. 2.2), is somewhat stiffer than polyethylene, primarily for reasons of rotational steric hindrance.

As the size of the side groups increases, so the height of the energy barrier to rotation increases. For n-butane, complete rotation requires about 20 kJ/mol. In poly(methyl methacrylate) the side groups are methyl and methyl carboxyl, and rotation would be expected to be much inhibited in comparison with polyethylene, an observation supported by the relative flexibility of the two bulk polymers (cf.Fig. 7§2.2). It should be evident, therefore, that the work required to extend a polymer chain depends to a large extent on the energy required to rotate each chain link.

•2.6 Bond geometry

It remains to be demonstrated that chain extension does indeed depend on bond rotation – that there can be no extension unless rotation does occur. This should be clear from Fig. 2.9. The angle between the bonds to a carbon atom when it has sp³-hybridization, the tetrahedral angle, φ, is given by:

< ?xml:namespace prefix = "mml" ns = "http://www.w3.org/1998/Math/MathML" />ϕ=2sin‐12/3=109.47…°then,a=−cos ϕ=1/3b=sin ϕ=22/3henced1=1+2a=1.666…=5/3andd2=4b2+d12=2.516…=19/3

henced1:d2::1:1⋅51

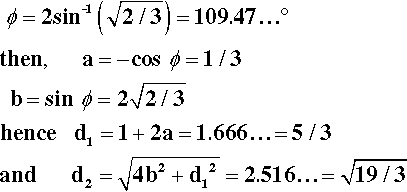
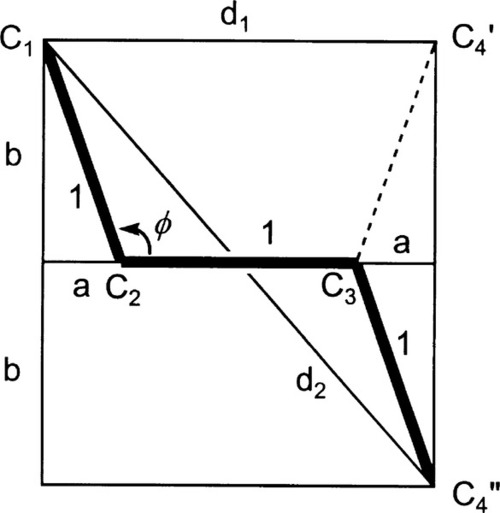
To put this in scale, the difference in the distance between C₁ and C₄ in its two extreme positions, d₂ – d₁, is just about 0·85 of the C-C bond length. Thus, a tensile force acting across C₁ − C₄ ′ must result in greater separation, and this must involve relative rotation of the intervening atoms, with their substituents, about all three bonds. It is therefore plain that any deformation of a polymer that results in a change in dimensions does so by doing work against the steric hindrance to rotation. It is also worth noting at this point that once the fully extended conformation has been attained any further deformation must be because of bond-angle and bond-length strain. In both senses, C-C bonds are very stiff in comparison with the work required for bond rotation. One would therefore expect a dramatic increase in elastic modulus once this point has been reached.

The fact of the central bond rotation can also be demonstrated with a molecular model (Fig. 2.10). Applying tension to the axial hydrogens (a, b) of butane in the eclipsed conformation, the relative positions of the hydrogens on C₂ and C₃ (x, y) can be observed to change. Thus hydrogen atoms x and y start out on the same side of the C₂-C₃ bond (they too are “eclipsed”, cf.Fig. 2.5), but end up on opposite sides, a full 180° apart, their positions having rotated in opposite directions relative to the tension axis. This can only have happened by rotation of the C-C bonds.

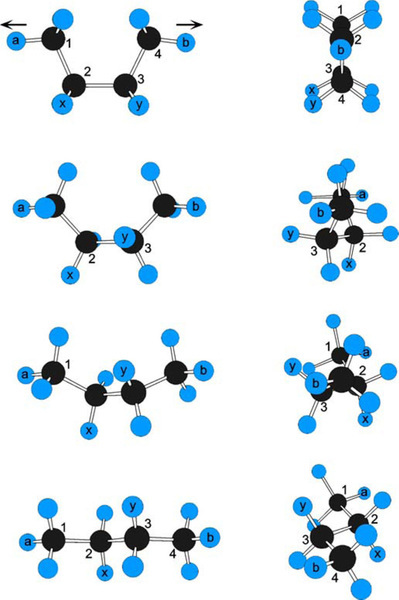
Notice also that the H_a-C₁ and H_b-C₄ bonds do not remain aligned. This is also due to rotation of the methyl groups about the C₁-C₂ and C₃-C₄ bonds, driven by steric interference with the hydrogen atoms on C₂ and C₄. Thus, for longer chains, such as illustrated in Fig. 2.4, rotation at any C-C bond has implications for the adjacent groups. The overall energy of the chain depends on all such effects.

•2.7 Activated process

It follows from the existence of energy barriers to bond rotation that the rate of crossing those barriers from one state to the next is a function of temperature, as temperature affects the vibrational and rotational energy of all bonds, as concluded at §2.4. Likewise, because deformations of the kind shown in Fig. 2.10 must occur sequentially in a process such as the chain extension of Fig. 2.4, they take time. Such time- and temperature-dependent rearrangements are an essential aspect of the behaviour of not just single molecules but of bulk materials as well, in their plastic deformation. These then are flow processes, and the characterizing property is viscosity.

§3 Viscosity

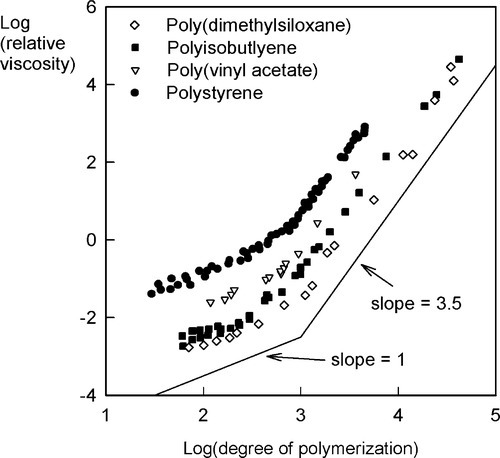
The viscosity of polymers, that for the moment we may simply describe as the ease with which liquid-like flow may occur, is much affected by the chain length.^[4] This is largely due to the fact that the longer the chain the more entanglements there can be. There will therefore be more resistance to the chains sliding past each other bodily (a process called reptation – movement like a snake), and so to gross flow since this will require many chains to move in such a way. There is a simple theoretical prediction that viscosity, η, is just proportional to the molecular mass for any given polymer system at a fixed temperature, i.e.

η∝Μ

Experiment, however, shows clearly that the actual effects are more complicated, and an equation of the form

η∝Μβ

is required to account for the data, with the exponent β never having the exact value 1. It usually takes a value somewhere between 1 and 2 for low degrees of polymerization, i.e. chains less than about 1000 units (mers) long. This effect can be explained by observing that the chain ends are much less entanglable than the rest. The terminal sections of the polymer chain are restrained at only one end, where they are connected to what may be termed the middle section. The ease with which a chain can be entangled therefore depends on the length of the ‘middle’, not the whole length of the chain; in other words the contribution of the ends to the overall viscosity is much less than would otherwise be calculated. The effect of increasing the degree of polymerization is consequently proportionally rather greater than expected, because the ends are effectively of fixed length, and we may consider that it is the ‘middle’ portion that grows, hence the value of β > 1.

•3.1 Entanglement

On the other hand, at degrees of polymerization greater than about 1000, the value of β is nearly always about 3.5 (Fig. 3.1). Without attempting to explain the precise value, this abrupt change indicates a critical entanglement chain length which is independent of the chemistry of the polymer (Fig. 3.1). Crudely, chains may now be tied in knots in such a way that slippage (reptation) caused by tension cannot unravel them. This critical chain length also corresponds to a critical point in the strength of such polymeric materials. Now, after a certain amount of deformation, the applied load will be borne by the primary bonds of the polymer chain, which bonds are much stronger than the van der Waals forces otherwise holding the chains together. There is no slippage possible that will allow the dissipation of that stress (i.e. relaxation). Hence, those primary bonds break rather than the chains becoming disentangled. A noodle analogy works here: short noodles separate readily, long ones must be broken when pulled because they become entangled.

Only gold members can continue reading. Log In or Register to continue