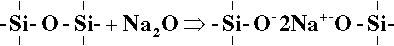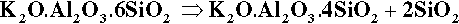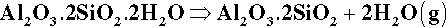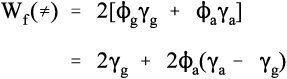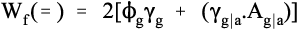Ceramics are capable of very high strength and stiffness (Figs 1§14.1, 2), and in general have low densities in comparison with metals. Their use may therefore offer considerable advantages. However, their often extreme brittleness (and thus flaw-sensitivity) limits their applications, and especially to circumstances where tensile loading – particularly through bending – is minimal or non-existent. Nevertheless, porcelain and similar ceramics are of great value in dentistry for one overriding reason: they can be made to resemble natural tooth materials extremely well indeed. Porcelain inlays, denture teeth and facings for metal work have low wear and high chemical resistance to oral conditions, while crowns can offer unsurpassable mimicry.^[1] Even so, there are problems which need to be overcome.^[2]

§1 Structure

Porcelains are composite materials. They consist of a silica-based glassy matrix embedding a core of various kinds of crystalline substance, primarily silica and silicates; but other minerals are possible and sometimes used. The utility of the composite structure lies in several distinct areas: strength, optical appearance, and fabrication. These are, of course, interrelated. Glasses on their own are very scratch- and flaw-sensitive, optically unlike tooth tissue, and would require casting to achieve the accuracy required for dentistry. This as a ‘one-shot’ technique has limitations, particularly severe when graded properties – mechanical or optical – are necessary. Casting can be used (see §9.1), but the end result is not a glass.

The strength and stiffness issues of composites have been dealt with before (e.g. 6§2), and are developed further below (§3); the optical issues have been explored in 24§5. The question of fabrication in dental contexts is a matter of adapting traditional techniques to the demands of dentistry.

•1.1 Historical background

Some background helps to understand aspects of the dental material. Pottery or earthenware is typified as terracotta (‘cooked earth’), which means that natural clays have been moulded as a wet paste, dried, then heated to a temperature that causes the mass to bind together as a strong body unaffected by rewetting. The particles of the clay have partially reacted, partially fused to give a porous structure that corresponds to the biscuit stage of dental porcelain (§4). The porosity is, however, interconnected so that the structure is permeable. If pottery is to hold liquid it must be glazed; that is, a glassy and impermeable layer is added. Stoneware takes this a little further, by raising the firing temperature, which increases the strength and hardness. Raising the temperature further still leads to porcelain. In general, porcelain is described as vitrified, meaning that much melting has occurred to create a glassy matrix. The porosity is thereby much reduced, and the structure is typically not permeable. The extensive glassy matrix now makes the mass much more translucent, as opposed to the dense opacity of pottery. The fact that porcelain tends to be prepared from white ingredients, for aesthetic reasons and the ease of further decoration, has no bearing on these structural definitions.

So-called true or hard-paste porcelain was developed in China, sometime in the Tang Dynasty (618 – 907 CE), from a paste prepared from pulverized partially-decomposed granite called petuntse (). This was therefore a natural mixture of kaolin (), feldspar and quartz. Subsequently, there have been many varieties of porcelain in which the proportions of the minerals have varied as well as the firing temperature, and other substances introduced into the mixture. These do not affect the broad description of porcelain. However, it will be seen that the extent of the melting (proportion of glassy matrix), the remaining porosity and the proportions of the minerals – the composition, are all important variables in determining the properties.

•1.2 Dental porcelain

Dental porcelain is not, in these broad terms, significantly different. In the final fired condition, it consists of a glassy alumino-silicate matrix (with various cations; §2, §7) in which are embedded several crystalline phases, in particular feldspar (§2), mullite (§2.1), alumina (§3), and quartz – which is part of the initial formulation and survives unreacted. Various minor phases of pigments (§7) are also present. The key structural aspect is that the matrix wets and bonds directly to each phase of the core, which confers the strength of the system. The presentation does differ: a dry powder which is to be mixed with water so that, using a small spatula, the desired shape can be built up incrementally, with vibration to help consolidate the mass (cf. 2§2.2, 4§7.9), when water is said to be ‘brought to the surface’, essentially as the density of powder compact increases. Excess water can be removed by absorbent paper so that the body does not collapse or slump (see 4§7.8). This technique, rather than moulding a plastic paste like clay for pots, permits the variation of composition from place to place in the structure such as to vary the opacity, strength and colour of the porcelain after firing. The powders may have organic dyes included in them to permit identification once they are in place on the restoration as it is built up. Being organic, these are intended to burn away on firing. But before we consider the firing reactions (§2) we need first to discuss the chemistry of the glassy matrix.

•1.3 Silica glasses

The random linking of [SiO₂] tetrahedra in fused silica has previously been described (Fig. 17§2.9), the links between the silicon atoms being the shared oxygen atoms. This glass can be considered as the parent structure from which other silica glasses are derived. Because each silicon unit is linked to four others we may describe this three-dimensional network as having a connectivity of 4 (22§2).^[3]Alternatively, this structure may be considered from the point of view of the frequency of cross-linking, the cross-linking density having the value 2, the excess over the minimum connectivity of a (linear) polymer of 2.

If any of these links were to be broken it would be necessary to add an extra oxygen atom in order to satisfy the valence requirements of one of the silicon atoms, which would otherwise be exposed. This in turn would leave the structure with excess negative charges which must be balanced by the inclusion of metal ions such as Na⁺. This is equivalent to reacting the silica with a metal oxide:

< ?xml:namespace prefix = "mml" ns = "http://www.w3.org/1998/Math/MathML" />‐Si||‐O‐Si||‐+Na2O⇒‐Si||‐O‐2Na+‐O‐Si||‐

Continuing this reaction further leads to a structure such as that represented in Fig. 1.1, which is now that of a plain ‘soda’ glass. As might be expected, any metal ions can be substituted for the sodium, and in endless mixtures, giving rise to a vast range of values for the properties. Some of this range was mentioned earlier (9§7), but other common varieties include ‘soda-lime’ glass, as used for windows and so on, which includes some calcium oxide; ‘crown’ glass, where potassium or barium oxide is substituted for the sodium; and ‘flint’ glass, which uses lead oxide.

The pure fused silica glass naturally does not possess an equilibrium structure. It would revert eventually to one of the crystalline forms if the activation energy for the conversion were available (17§2.3). Similarly, fused mixtures of metal oxides and silica would separate out into distinct crystalline phases if allowed to do so (Fig. 1.2): at equilibrium all mixtures of Na₂SiO₃ and SiO₂ would result in crystals of those two compounds only.^[4] But this would require extremely slow cooling (geological timescales!). Under normal circumstances of moderate rates of cooling amorphous glasses (Fig. 1.1) are always produced. This is because to form crystals requires covalent bonds to be broken followed by diffusion in a viscous medium. Here, then, is another example of kinetics limiting the approach to what the thermodynamics demands.

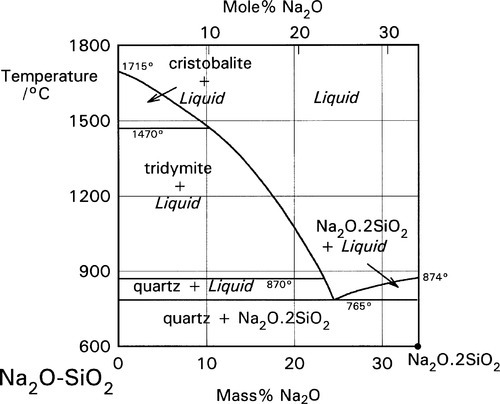
One circumstance where devitrification is encountered is in glassblowing, where repeated heating and plastic deformation of the viscous mass can cause nucleation. The crystals then tend to grow quite quickly, rapidly making the glassware very weak as well as brittle, therefore useless.

There are two important consequences to arise from dissolving metal oxides in silica glass. Firstly, there is a substantial lowering of the melting point (cf. Fig. 1.2). Rather, since it is a glass, we should refer to the softening point (see §4.6). This enables working with materials that otherwise would be extremely refractory. Secondly, and obviously connected with the first point, the viscosity of the melt is also considerably lower because the presence of the metal ions has resulted in broken chains and lower network connectivity (cf. 22§2). More than this, the negatively charged ‘oxide’ oxygens may encourage bond exchange by further lowering the activation energy for bond breaking, attacking existing bonds. Such events are essential for a cross-linked network system to flow at all. This may be compared with the stress-relaxation mechanisms operating in rubbery impression materials (Chap. 7).

•1.4 Aluminium

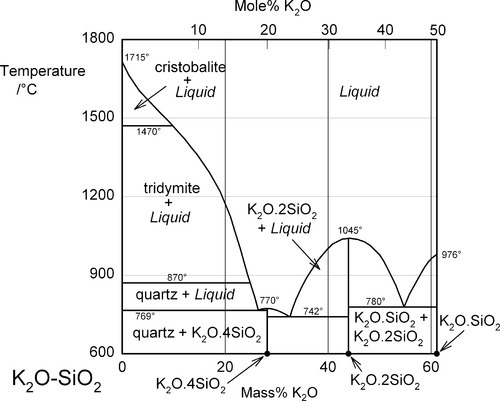
Aluminium is an important element in the context of silica chemistry because of its ability to substitute for silicon in silica and silicate structures. This has previously been discussed in connection with cements (9§7.3), but it is also responsible for the huge range of compositions and structures in the aluminosilicate minerals. It should be remembered that the charge associated with the presence of the aluminium is different (one more negative charge) from that for silicon, so that an extra balancing metal cation charge must be present for every Al atom included if the structure is to remain simply substitutional. Otherwise, an oxygen atom must be removed, which thus requires the formation of a bond (the reverse of equation 1.1). An example of such a system is that of Al₂O₃ – K₂O – SiO₂ (Fig. 1.3). ^[5] This is of importance because it includes a range of compositions corresponding to those used in dental porcelains. Again, this is an equilibrium diagram, whereas it will be seen that normally dental porcelain is far from equilibrium.

The phase diagram of Fig. 1.4 is another example of juxtaposed binary systems: SiO₂ – K₂O.4SiO₂, K₂O.4SiO₂ – K₂O.2SiO₂, and K₂O.2SiO₂ – K₂O.SiO₂, reading from the left, where the boundaries between these systems are the intermediate compounds, each of which shows a sharp melting point. In this case, the mixtures are all eutectics. For comparison, Fig. 1.2 shows only one eutectic mixture of a kind similar to the binary systems here.

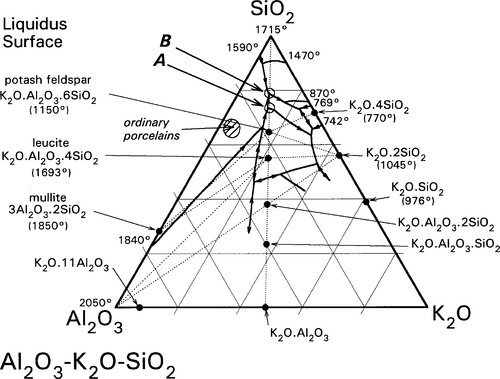
The K₂O – SiO₂ system, corresponding to the right, upper edge of Fig. 1.3, is shown in Fig. 1.4. From this it is apparent that the system is a little more complicated than in Fig. 1.2, but the lowest eutectic temperature is even lower at about 742 °C. What this also illustrates is that a variety of compounds may be involved in the chemistry of the firing process for porcelains and similar materials, according to local conditions. That is, given a mixture of reactants, which can be expected to react slowly, reactions at interfaces may not represent an overall process or move towards overall equilibrium, at least initially. Time, temperature, diffusion rates and reaction rates, as well as thermodynamics determine the outcome – kinetics is extremely important.

•1.5 Labelling convention

A convention commonly used in this field needs introduction. In the phase diagrams discussed so far there have been only two kinds of product representation: either elemental solid solutions or definite stoichiometric compounds, such as Ag₃Sn or ZnHPO₄. The substances represented at the corners of the diagrams, i.e. at the ends of the composition lines, the components, are then seen as being combined in a natural manner.

However, in ceramic work, where glasses are very often involved, quite clearly stoichiometry is very frequently not a relevant consideration except for the occasional crystalline substance. It is therefore not sensible to talk in terms of mixtures such as “Na₅AlSiO₆” as if they were compounds, which clearly have no chemical meaning. Rather, it is convenient to speak in terms of multiples of the component oxides, viz. 5Na₂O.Al₂O₃.2SiO₂ for the above example, and even for good chemical compounds, whilst recognizing that the oxides do not exist as individual molecules in either the melt or the glass. This is essentially a matter of practical utility – it is easy to locate compositions in diagrams, and awkward sums are avoided. In addition, it ensures that the underlying stoichiometry of the oxides is preserved, since no variation in relative oxygen content is meaningful. Given this symbolic convention it is now easier to discuss some of the reactions of dental porcelain.

§2 Firing Reactions

It is apparent from Fig. 1.3 that, even with just the three components, many crystalline compounds are possible at equilibrium. However, certain regions (i.e. ranges of composition) are capable of producing quasi-stable glasses on cooling from the melt. Typical porcelain, as in art work and domestic ware, has an overall composition close to K₂O.5Al₂O₃.20SiO₂, rather richer in silica and potash (K₂O) than earthenware, which is based on clays. Dental interest centres around the mineral potash feldspar, K₂O.Al₂O₃.6SiO₂. This compound melts peritectically at 1150 °C to produce the compound leucite:

K2O.Al2O3.6SiO2⇒K2O.Al2O3.4SiO2+2SiO2

This reaction is better understood by examining the vertical section (the isopleth) of Fig. 1.3 taken between the leucite point and the SiO₂ apex (Fig. 2.1). The co-existing liquid at the peritectic temperature has a composition corresponding to A in Fig. 2.1, approximately K₂O.Al₂O₃.9SiO₂, i.e. the silica ‘ejected’ from the structure may be thought of as dissolving a proportion of the leucite formed in that decomposition reaction. The most significant point to arise from this, as remarked above, is the dramatic lowering of the effective melting point of the silica in the presence of the other oxides. Indeed, silica in excess of that required to form feldspar actually melts at 985 °C, which is the ‘eutectic’ temperature of the pseudo-binary system (B in Fig. 2.1); the liquid here has a composition approximately K₂O.Al₂O₃.12SiO₂.

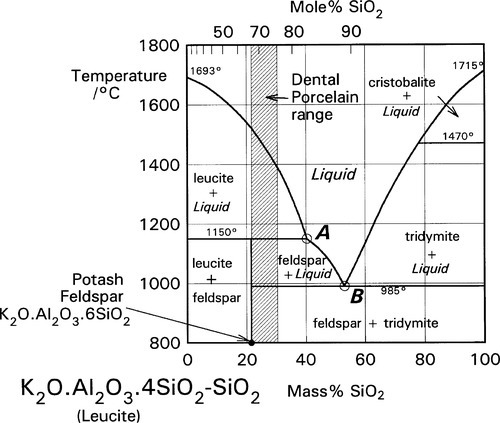
A certain proportion of sodium, a small amount of rubidium, and even occasionally some calcium, may be found in natural feldspar. These metal substitutions will tend to lower the eutectic and other transformation temperatures in this system. In addition, the sodium analogue of potash feldspar, albite, Na₂O.Al₂O₃.6SiO₂, may also be added to mixtures for dental porcelain, with similar effects.

•2.1 Kaolin

A typical dental porcelain will mainly consist of a mixture of feldspar with, say, about 15 – 20% powdered quartz and a few percent of kaolin as a binder. Kaolin is an hydrated clay mineral, Al₂O₃.2SiO₂.2H₂O, and is in the form of very fine hexagonal plates in the range 1 – 5 μm diameter and about 1 μm thick. Because of the presence of strong surface charges on these particles (which are mutually repellent) they form colloidal suspensions in water, binding large amounts of it, and can be used to provide a certain amount of coherence and plasticity to a porcelain powder slurry, facilitating the handling. The effect otherwise would be like wet sand: surface tension holds together a sandcastle (Fig. 2.2), but it is a very fragile structure. The presence of some clay-like mud in the mixture makes it much tougher (but only when the powder is wet). The amount of kaolin in dental porcelain must be limited, however, because of the resulting opacity in the product; tooth-like appearance depends much on translucency. The coherence of the porcelain powder, like the sandcastle, otherwise depends entirely on the capillary forces acting in the films between grains, and thus clearly depends on a minimum amount of water being present. Recall that gypsum and investment slurries only flow well when glossy; after ‘loss of gloss’ they are much stiffer. Excess water must therefore be carefully blotted away during the manual build-up of a porcelain restoration. This water must, of course, be carefully removed by drying slowly with gentle heat just before firing to avoid wrecking the structure.

On firing a dental porcelain the first important reaction is the dehydration of the kaolin at about 450 °C:

Al2O3.2SiO2.2H2O⇒Al2O3.2SiO2+2H2Og

The solid product is called metakaolinite (Fig. 2.3). This is in fact an unstable substance (not a true compound) which, by being finely divided and amorphous, is relatively reactive. Its composition lies in the silica – mullite two-phase field. On further heating to about 1000 °C or so, therefore, this material decomposes to mullite, 3Al₂O₃.2SiO₂ (which is a well-characterized, definite compound), and amorphous silica. This latter remains reactive because it is still finely divided as well as having a non-equilibrium structure. The mullite will be well-crystallized, as it is above its recrystallization temperature (cf. 11§6.6) of 918 °C.

As the temperature is raised further still, the feldspar now starts to melt and decompose at ~ 1150 °C (reaction 2.1), and not at a lower temperature despite the presence of the free silica, because the reactions are so slow and equilibration can never be achieved on practical timescales. The liquid formed will flow and start to cause the consolidation of the powder particles because of its own capillary action (10§2). Reactions with the amorphous silica and mullite now start to occur, and metal ions from the feldspar start to react with the quartz powder particles originally included, but which up to now have not altered at all except for the α-β transition at ~ 573 °C (Fig. 17§2.2). On cooling this partially-melted mass, crystallization of the liquid does not occur because of the viscosity of the liquid phase and the high activation energy of crystallization. The final structure now is a glassy silicate matrix embedding a core of a mixture largely of quartz and unreacted feldspar, with a dispersion of the separated mullite.

•2.2 Processing temperature

The above scheme is applicable to the so-called high-fusing dental porcelains, where little if any glassy phase is present initially. However, the melting point of the mixture has been lowered by the partial reaction of the components, so that on refiring the onset of melting and further reaction occurs at a lower temperature, even though the overall composition is unchanged. The low- and medium-fusing dental porcelains are prepared in just this way, by controlled reheating of already-fired porcelain. After cooling, usually by pouring the mass into water to induce much cracking by thermal shock (steep stress gradients caused by rapid cooling of the low thermal conductivity material, §5.5), the mixture is ground again to a fine powder, which is then essentially the commercial product.

There are thus two ways of controlling the temperature required for processing a dental porcelain: the composition and the degree of reaction permitted in previous firings. The successive-increment procedures employed in porcelain restoration fabrication are dependent to some extent on the existence of a group of products with a range of fusion temperatures being available. But, equally, excessive refiring of any such material can be deleterious because this permits the reactions to go a little further towards equilibrium and therefore the possible formation of undesirable crystalline phases, which may be expected to alter the optical and mechanical properties.

•2.3 Pyroplastic flow

In addition to the chemical changes, excess ‘time at temperature’ will also result in the lowering of the temperature at which distortion due to sagging or slumping can occur. This is known as pyroplastic flow. Clearly, this needs to be avoided if the shape of the restoration is to be maintained. Nevertheless, there is a tradeoff between resistance to this deformation and the sintering process (§4). Partly, some tuning of behaviour can be made by the manufacturer by adjustment of the composition: thus for a given total amount of alkali metal ions, K₂O increases the viscosity while Na₂O decreases it. There are complementary changes in the melting points: lower for using sodium in preference to potassium. It should be plain that the quality of the work depends on accurate control of temperatures and times, i.e. following the instructions.

§3 Alumina Strengthening

As the quartz originally included is a relatively coarse-grained material and reacts only very slowly (if at all) at the kinds of temperature used, this component remains as a distinct crystalline phase in the glassy vitrified matrix. Hence, as mentioned above, porcelains are composite materials and much of their strength is due to this structure. Quartz, however, is not a particularly strong material. Considerable improvement in porcelain strength has been obtained by using alumina in the same role. Alumina has an extremely high fusion temperature (Fig. 2.3) and can be expected to react only very slowly indeed with any matrix, although there will be some reactions on the surface which will tend to bond it covalently to the matrix, which is desirable.

Accordingly, aluminous or high alumina porcelain consists of about 50 mass% Al₂O₃ in a typical low-fusing glass matrix. The extraordinary strength of alumina is thus utilized in the composite. However, care must be taken to match closely the thermal expansion coefficient of the matrix to that of the alumina; this will be done by adjusting the mix of metal oxides used. If the match is not good, thermally-induced shear stresses developed at the interface (on cooling after firing) may lead to a weakened bond between the two and a fracture path which follows the periphery of the particles. The bond is relatively weak because of the limited reaction referred to above. If the shear stresses can be avoided the fracture will be tend to be transgranular and the overall strength will depend more on the fracture energy of the alumina. Clearly though, the balance is a fine one as the total surface energy for a complicated fracture path may be only slightly more than a straight fracture through zones of sometimes higher surface energy of formation.

•3.1 Fracture energy

We can try to understand this kind of system by writing out the overall specific fracture energy W_f in terms of the surface energies γ_g and γ_a of the components, glass and alumina. To start, we write down the fracture energy for the glass alone, which is effectively for a transgranular path (indicated by the symbol ≠) because there are no other phases involved:

Wf≠=2γg

This is the familiar expression of the work of creation of a crack (cf. equation 10§1.10); the factor of 2 is because we are counting both new surfaces (10§1.2). Since the proportions of each type of surface in a random plane section through an alumina-in-glass composite are the same as the volume fractions, ϕ, of each phase, we can then write down directly the fracture energy for a random plane transgranular crack:

Wf≠=2[ϕgγg+ϕaγa]=2γg+2ϕaγa‐γg

From this it can be seen that if the work of fracture of the alumina is higher than that of the glass then the overall work must be higher – which is true. (The square bracketed expression is, of course, a simple mixture rule, cf. 6§2.6.)

Similarly, we consider a crack that crosses the glassy matrix directly but deviates around the alumina particles, that is, peripheral fracture. This must be an interfacial failure (symbol =) between the glass and alumina (g|a). Thus, we have:

Wf==2ϕgγg+γga.Aga

where γ_g|a is the work of fracture of that interface, whose relative area, A_g|a is at present unknown. However, for simplicity, we can assume that the alumina particles are spherical and that the crack is aligned with a diameter. The interfacial area between a spherical particle and the matrix on one side (4πr²/2) is then exactly twice the area of the diametral cross-section (πr²) of that particle. If it can also be assumed that the energy of formation of the two new surfaces, i.e. glass and alumina, each have about the same energy whether from the homogeneous material or the interface, we have from equation 3.3:

Wf=≈2[ϕgγg+ϕ