Whilst the casting process has a long history, and the skills needed for successful casting can be learned by trial and error, it is essentially the properties of the alloys that control the outcome. The market these days is characterized by an enormous and potentially bewildering array of very similar products, even from a single manufacturer. To begin to comprehend the reasons for design choices it is necessary to consider some of the alloy systems in greater detail. However, it is also necessary to point out that in many cases the alloys themselves have often been designed by trial and error, and a comprehensive explanation of their behaviour in suitably scientific terms is simply not possible because the essential data have not been gathered. Nevertheless, it is not too difficult to outline the generic properties of the major classes.

When choices of casting alloy are to be made it is primarily the application that provides the guide in that strength, stiffness, density (as it affects the mass of a suitably strong or stiff framework, for example), ductility, suitability for porcelain bonding, and so on must first be considered. A second level of importance is that of the experience of the dental laboratory in handling that alloy. As has already been made plain, the outcome of the entire casting process depends on the combination of investment and alloy, with all the many handling and processing variables that this entails. But, despite the theoretical matching of these factors, it still requires a demonstration that the entire system works to give an acceptable outcome. Part of the system is the skill of the technician in running a process consistently, and being able to calibrate it, as it were, to tune critical steps to ensure success.

Pure gold is the outstanding restorative material. Because of its peculiar combination of properties: tarnish resistance, ductility with work hardening, and the ability to be cold-welded by pressure alone, it is usable as a direct filling material in the form of foil or powder (28§4) (although the skill, effort and expense of this process has led to it being more or less abandoned now). Aided by the deep-rooted and ancient mystical associations for the metal, its colour does not present aesthetic problems for many people, despite the great contrast with tooth material. As has been implied elsewhere (Chap. 24), the patient’s perceptions are at least as important as more fundamental criteria for material selection.

However, in its pure state, gold is not very strong for applications other than inlays, i.e. for crowns, bridges and removable partial dentures. The strength advantages of alloys are required, but these require casting rather than direct fabrication techniques. This, of course, precludes work hardening as a means of increasing rigidity because dimensional stability requirements are severe if fit is to be maintained. Recourse to hardening and strengthening by suitable alloying elements must be made.

•1.2 Solid solution hardening

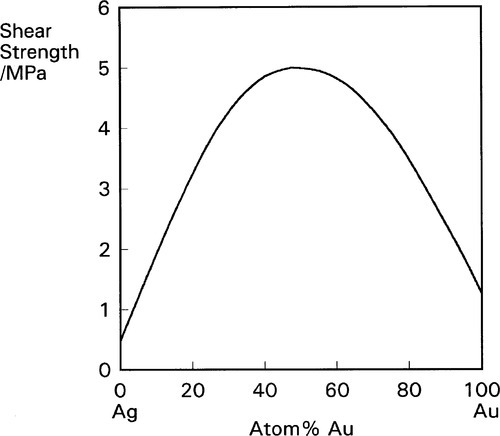
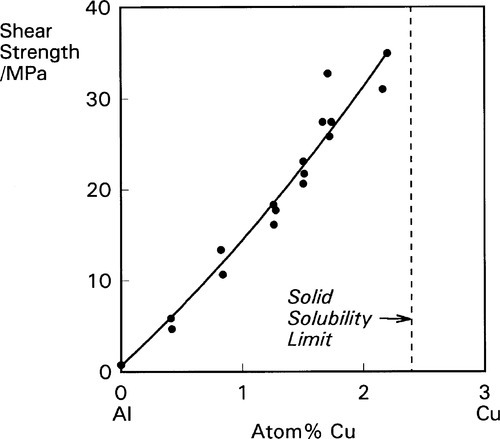
The disorder introduced into crystal structures by elements in solid solution has previously been discussed in terms of the ease or otherwise of slip along certain planes of atoms (11§5). The effect is only moderate when there is a close match of atomic radii, as is exemplified by the Ag-Au system (radius ratio 144/143 = ~ 1.01) (Fig. 1.1). But even so, at an atomic ratio of ~ 1:1, when the disorder might be expected to be at its greatest, there is an appreciable peak in the strength. By way of contrast, with Al-Cu α-solid solution alloys the effect is much more pronounced because the radius ratio (143/128 = 1.12) is very close to the general practical limit for a continuous solid solution, and the distortion is much greater (Fig. 1.2).^[1] Indeed, the solubility limit for Cu in Al is 2.5 at% at 548 °C. The ratio for Au-Cu (144/128 = 1.13) is also close to that limit, and while a continuous solid solution is formed above ~ 400 °C, i.e. at all compositions, distinct new phases in fact form below that temperature (Fig. 1.3).^[2] Of particular interest are those corresponding to stoichiometries around AuCu₃ and AuCu, but it is the latter which is the phase of principal interest in dentistry. A peak in solid-solution hardening is again observed at this atomic ratio (i.e. 1:1).

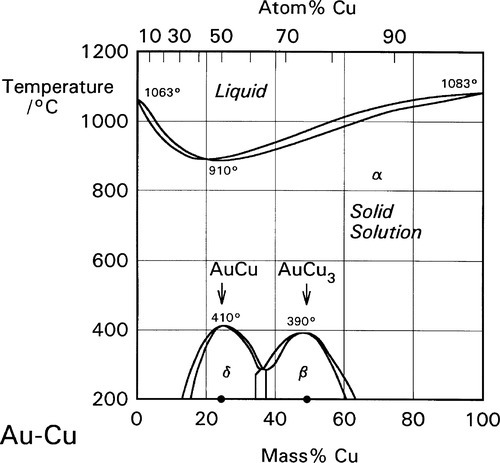
The crystal structure for the whole Au-Cu system is essentially f.c.c. (11§3) and, in common with many other solid solutions, the α-phase is one of random substitution (Figs 1.4a, 1.5a). That is, at any point in the lattice of an α-phase alloy of composition AuCu, the probability of finding either kind of atom is exactly 0.5.

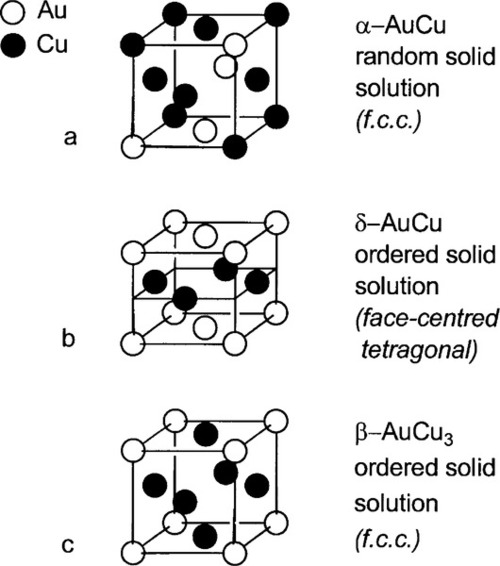
•1.3 Ordered phases

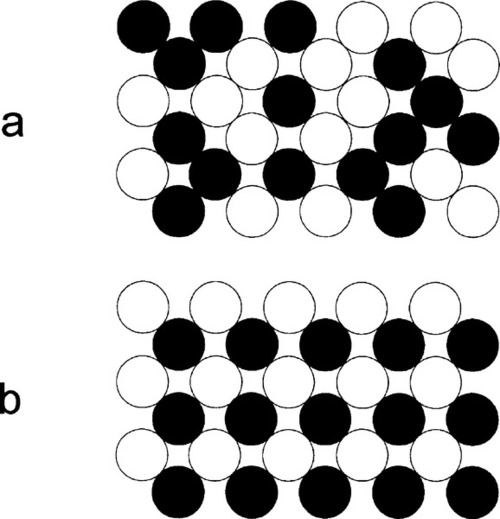
In δ-phase AuCu the structure is ordered. The Au and Cu atoms alternate regularly, which is equivalent to alternating layers of Au and Cu atoms (Figs 1.4b, 1.5b), in a pattern that repeats over long distances. In contrast, a random substitutional solid solution does not have long-range order for the occupancy (element identity) of each lattice site, although the probability of finding a particular kind of atom is fixed at the overall atomic proportion for the phase. Such a structure arises because the layers fit together just a little more compactly, increasing the regularity of the structure, thus lowering its energy. This rearrangement results in a slight distortion from a perfect cubic lattice to a tetragonal one, in which one of the three unit cell dimensions is smaller than the other two (the vertical direction in Fig. 1.4b), the ratio being about 0.935. This structure can be seen to consist in effect of two interlaced lattices, in this case of identical pattern: one of Cu only, the other of Au only (Fig. 1.6). This type of structure is known as a superlattice and is characteristic of ordered solid solutions. Alloys of the composition AuCu₃ produce a similar ordered, low-temperature phase (β, Fig. 1.4c) in which the Au atoms are placed at the corners of the f.c.c. lattice and the Cu at the faces. However, the lattice constants, the unit cell dimensions, are not appreciably different from those of the α-phase in this case, and this phase is of no particular dental interest.

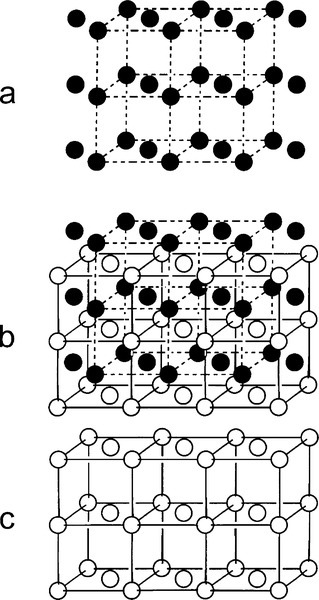
It can be seen that the close-packed planes of the f.c.c. structure (albeit with some irregularity because of the random substitutions of the solid solution) are taken further from ideality by the tetragonal distortion. Slip is therefore more difficult because the principal close-packed ‘planes’ (normal to the cube diagonals, Fig. 11§3.23) are not quite planar. This means that for this reason alone δ is harder than α-phase at the same composition, an effect that does not operate for β-phase.

The significance of the ordered solid solution δ-phase, and its importance to dentistry, lies in the fact that it produces a structure markedly harder than just α-phase. While this makes such an alloy much more suitable for use in the dental context, it also allows a special kind of heat-treatment to be used to develop the degree of hardness required for any particular application or, conversely, to permit softening for adjustment which is then followed by rehardening. This process is enhanced by a further source of hardening.

•1.4 Coherency strain hardening

If an alloy with the composition AuCu is cast, rapid cooling or quenching to around room temperature will preserve the high-temperature, random, solid solution structure of the α-phase. There will be little segregation (12§1) because the liquidus and solidus are very close together. But if the temperature is then raised again and held below that of the upper limit of the boundary of the δ-phase field (at, say, about 400 °C), equilibration will now occur by diffusion, and the superlattice structure will tend to form. The higher the temperature the greater the diffusion rate, because diffusion is a process requiring an activation energy. But because there is a change in unit cell dimensions, notably a reduction in the direction of the c-axis, with concomitant slight increases in the other two directions, the transformation produces a strain in the lattice.

The initiation of the α to δ phase change will take place at a large number of separate locations within any grain randomly and independently. This will necessarily be with random orientation of the tetragonal c-axis along any of the three axes of the original cubic structure. These regions of differing c-axis orientation within a given grain are called domains. Taken over a large enough region the net strain in each grain will average out to zero, and there will be very little volume change overall. But the variation from one orientation to another from place to place within the grain superimposes on those primary grains a microscopic lamellar or granular structure, and it is this that makes the heat-treated material hard. There are now effectively very many more grain boundaries, i.e. between domains, so dislocations travel much shorter distances before their movement is inhibited. There is less slip. The formation of β-phase does not cause a similar hardening because there is no associated axial dimensional change to induce strain. The δ-phase hardening process is entirely reversible: reheating above ~ 400 °C again produces the α-phase, which may again be preserved by quenching.

From another point of view, we can see that it is the periodicity of the structure in the δ-phase which is varying. The crystal lattice does not repeat indefinitely in any direction, but every so often skips a step, as it were. The boundaries between areas of different phase (in this wave periodic sense, not the structural-constitutional sense) are strained, since the spacing between layers and along rows differs slightly across a domain boundary. This then is known as coherency strain. Slip through such boundaries is therefore more difficult, that is, there is coherency strain hardening. Fig. 1.7 shows what a random section through the junction between four such domains might look like. Since the spacing of the atoms in each kind of domain is different from that in its neighbour, the mismatch generates the strain.

Although δ-phase is expected to be a little harder because of the tetragonal distortion, on top of what would be expected from the substitional effects, this on its own is not very great. Most of the hardening is due to the coherency strain; the superlattice by itself does not confer the observed change, which is largely due to the domains forming with random orientations.

Current gold alloys for dentistry may consist of 6 or more major constituents: Au, Cu, Ag, Pt, Pd, Zn; several other minor additions may also be made. Clearly, the multi-dimensional phase diagram for such a system is going to be extremely complicated, and full details are not at present known for any such system. Detailed explanation of the purpose and effects of any single alloying element in such contexts cannot be given, even though sometimes rather vague statements may be made. However, certain aspects and broad principles can be summarized, and these are applicable no matter which alloy is under consideration.

•1.5 Precipitation hardening

When a second phase is allowed to separate from (usually) a high-temperature solid solution (see Fig. 12§3.9), those new precipitated crystals form randomly throughout the original grains of the alloy. They therefore get in the way of dislocation movement, limiting slip. Such alloys are described as being precipitation hardened. The example of the Ag-Cu system has already been discussed (Fig. 12§3.1). There, for example, the separation of the β-phase (solid solution of Ag in Cu) from a high temperature, Cu-rich α-phase (solid solution of Cu in Ag) at a temperature below the solvus results in just such a very fine-grained precipitate. Conversely, a heat treatment above the solvus will redissolve the precipitate to form a solid solution again. Reactions similar to these will play a part in the overall hardenability of such alloys. Time and temperature are the two important aspects of any heat-treatment: to determine the extent of any change, and the direction and rate of that change.

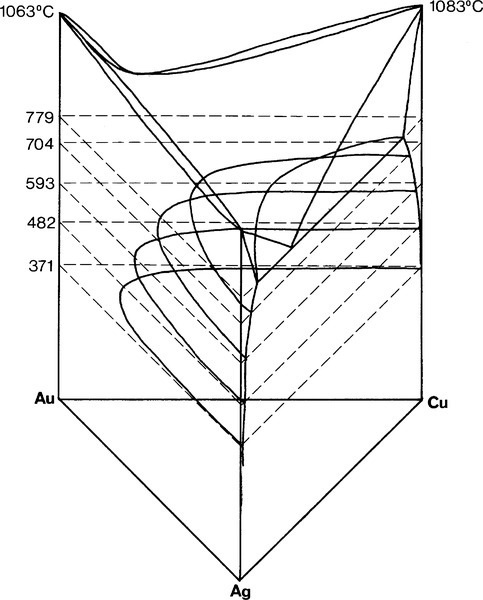
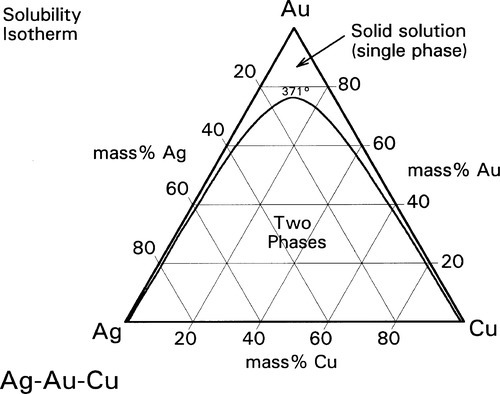
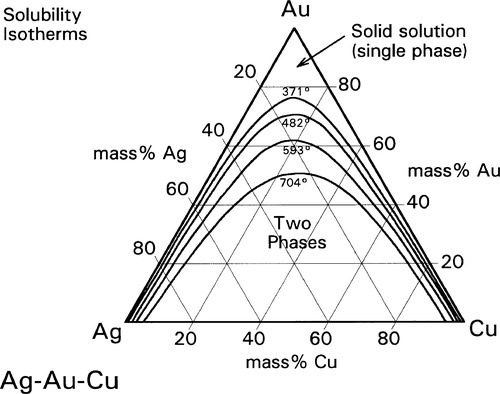
A continuous solid solution characterizes Ag-Au alloys (Fig. 12§1.11) as it does Au-Cu at high temperature, but in the ternary system Ag-Au-Cu below ~ 400 °C this is restricted to the very edges of the diagram (Fig. 1.8). (We shall ignore for the moment the formation of β and δ-phase Au-Cu superlattices.) However, as the temperature is raised the gold-rich boundary of the two-phase field (Au,Ag) + (Au,Cu) moves steadily towards the Ag-Cu boundary; at the same time the Ag- and Cu-rich solvi move away from the corresponding pure metal corners (Fig. 1.9). The two-phase field can be visualized as a dome-shaped volume in the full phase diagram (Fig. 1.10). Note that the faces of the prism are the three, two-component phase diagrams (cf. 14§3.7).