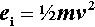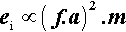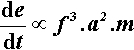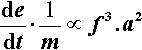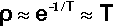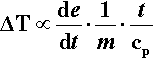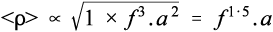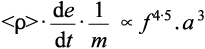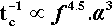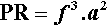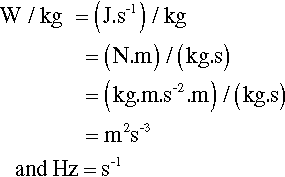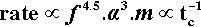Many dental materials, such as plaster, cements, and impression materials, must be mixed before use. The reason is obvious enough: the mixing of the two parts initiates a chemical reaction which develops the desired properties; that is, they set. The primary demand of mixing is also fairly obvious: the mixture must be intimate for even and complete reaction. But, given that, the time taken must be short to keep the working time long, i.e. keep the extent of reaction at the time of use low. Often consigned to an assistant as if it were a menial task, proper mixing is, however, usually critical to the success of a material and attention to detail is essential. In order to train an ancillary (assuming they are not already professionally-trained), or simply to ensure that standards are maintained, the demands and limitations of the various mixing processes used in dentistry should be understood. The peculiarities of zinc phosphate cement have already been dealt with (9§5), but we proceed now with some further aspects of mixing, which has more to do with machines and product selection than training, but all of which affect the quality of the outcome. Little effort is required, only attention to detail.

§1 Amalgamation

Liquid mercury reacts rapidly with several metals, wetting and spreading quickly over a large area as it reacts. Gold jewellery such as rings and watches are particularly prone to being rendered silvery by contact with stray droplets of mercury whether in the clinic or in a laboratory, and for that reason one is well-advised not to wear such adornment when mercury is around – advice that should be passed onto one’s dental assistant. Any treatment to remove the mercury from the gold is necessarily drastic, and the piece may not survive unscathed. Silver, as has been seen (14§1.1), is also reactive to mercury, but ordinarily may not appear to be very much so because of the presence of a fine film of sulphide (Ag₂S) from exposure to hydrogen sulphide in the air and to other sulphurous materials. This may prevent immediate metal-to-metal contact and so delay reaction until some rubbing breaks the film, in much the same way that the extremely rapid oxidation of amalgamated aluminium cannot be demonstrated until the oxide coat is broken under the mercury. In the case of silver, the sulphide coat is not very strong and usually not very thick, so that little effort is required to initiate reaction.

•1.1 Need for trituration

Certainly, when amalgam fillings were being placed by the showmen of the travelling medicine shows in North America in about the 1840 s, the powder from freshly-filed silver dollars reacted readily enough that amalgam could be mixed effectively (if a little alarmingly, given current awareness) in the palm of the hand. When tin, and then copper, were incorporated into silver-based alloys that were delivered to the dentist as a ready-prepared powder, this changed. Firstly, the powders were exposed to the air long enough that sulphide tarnish could develop, but secondly, the less noble copper and tin are much more readily oxidized. The bulk metals steadily acquire an oxide coat and no less in their alloys, especially tin, being the more reactive of the two. Thus SnO₂, CuO and ZnO may be found in addition to Ag₂S. These corrosion products prevent contact between mercury and alloy and thus prevent reaction (Fig. 1.1). Amalgam alloy had therefore to be mixed a little more vigorously, and this was achieved with a mortar and pestle (Fig. 1.2). This process has commonly been referred to as trituration, and involves a grinding action intended to disrupt surface coatings and even break or plastically deform the alloy particles, which actions would also expose fresh metal to the mercury as well as create dislocations that would raise the energy and thus the reactivity. With the finding that alloys should be ‘aged’ to reduce and stabilize their reactivity (14§3) to obtain a more consistent and sensible setting rate, the problem was exacerbated. The ageing was done at an elevated temperature in air or water, both of which are conducive to the oxidation of tin.

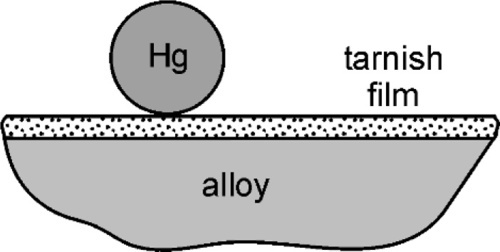
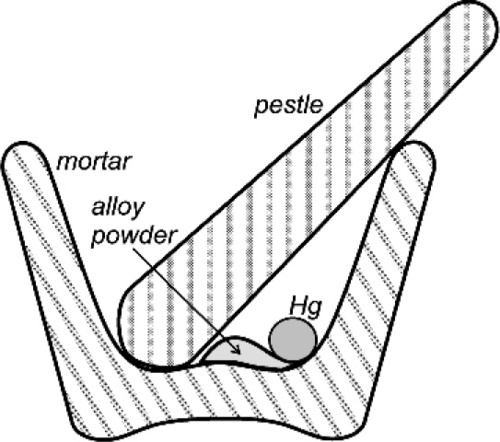
The fact that the main purpose of trituration was the abrasion of the tarnish coat to expose clean metal is readily demonstrated. If a commercial amalgam alloy powder has a droplet of mercury dispensed onto it, nothing will happen. Maybe after some minutes or hours it will have been absorbed by the powder, but on a timescale of interest to a dentist essentially nothing changes. However, if the alloy is first washed in dilute hydrochloric acid to dissolve oxides and so on, thoroughly rinsed and dried and the test repeated, the result is dramatically different. The instant that the mercury droplet is delivered, wetting and reaction start. Whilst alloy powders could be prepared oxide free, and could be stored dry and sealed against the air, extraordinary precautions would be necessary and these would probably be considered uneconomic. It is therefore always necessary in practice to apply sufficient friction to disrupt the oxide coat. Again, the presence of that oxide is easy to demonstrate, and in a very simple manner. Merely inspect the pellet of amalgam produced from a current mixing machine (for it should no longer be necessary to use hand mixing) and one may notice a fine grey powder, perhaps covering the pellet, or loose in the capsule. Since it is not wetted by mercury it tends to get excluded from the consolidating amalgam, becoming visible evidence of the tarnish. The older the alloy, and the poorer the conditions of storage, the more oxide.

Hand-mixing is a relatively slow process, and of low efficiency. As a result it required the use of extra mercury which then had to be squeezed out of the mix, through gauze or chamois leather, or later on with a special press, at the chair side prior to condensation. Inevitably there were problems of non-uniformity arising from the difficulty of a consistent squeeze, as well as from the mixing process itself. Even so, the remarkable efficacy of amalgam as a restorative material is underlined by its success, measured by its durability of many years, despite these difficulties.

The introduction of mechanical mixing was with the aim of obtaining greater speed and uniformity of mixing, but this also reduced the amount of mercury required for a plastic mix and thus eliminated the need to squeeze. However, the design of so-called amalgamators was on a pragmatic rather than theoretical basis and consequently their development has been unscientific. For example, many machines were designed to work by an oscillating motion causing the alloy and mercury to be thrown about with a small, often metallic object, again called a pestle (Fig. 1.3). There appears to have been a conscious effort to mimic the old mortar and pestle (Fig. 1.2), in the belief that as the mix was thrown against the ends of the capsule, the pestle followed and did the ‘trituration’.¹ It led to such claims as that the heavier the pestle, the better the mixing. This culminated in a short rod of solid tungsten weighing 8·5 g being sold as a pestle. The main effect of the use of this was the smashing of the ends of the capsule and the premature wear of the mechanism of the mixer. The danger of the bullet-like escape of such an object from a disintegrating mixing capsule is not to be dismissed, to say nothing of the mercury spread all over the room (28§6). The haphazard designs of machine and capsule also lead to such disconcerting events as the total failure of some products to mix at all on some machines, whether disposable or pre-dosed capsules. To overcome this, faster machines were designed. At least, their mechanisms were designed to move more quickly, as it was again assumed that only higher velocities were necessary. A simple analysis of the system reveals the fallacies of these designs.^[1]

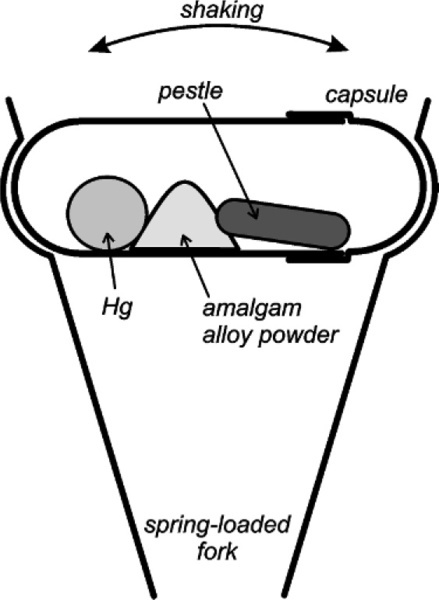
§2 Amalgam Mixer Analysis

Mechanical amalgam mixers essentially consist of a small cylindrical capsule into which is put the amalgam alloy powder and the mercury, and which is then shaken, typically end to end. The mechanism for producing this motion also resulted in various other motions, but these are relatively insignificant. So, ignoring the pestle for the time being, the kinetic energy, e_i, of each individual impact of the mix with the capsule end wall can be written:

< ?xml:namespace prefix = "mml" ns = "http://www.w3.org/1998/Math/MathML" />ei=½mv2

where m is the mass of the mix, and v the instantaneous collision velocity. While the mix is still powdered, all of this energy may be absorbed, i.e. this will be an inelastic collision. The mix as a whole will not bounce since interparticle collisions will rapidly randomize their directions of motion. It would be like throwing a handful of sand at a wall – single grains may bounce, but the whole assembly does not. Since v will be directly proportional to the frequency, f, and the amplitude, a, of the capsule motion (s^– 1 × m), no matter what the oscillation waveform (although it is usually close to sinusoidal), we may write (since we do not care about the constant of proportionality):

ei∝f.a2.m

Since an impact will be expected at each end of the capsule, i.e. twice per cycle, the number of impacts per second is expected to be twice the oscillation frequency, so that multiplying expression 2.2 by f gives the relative rate of energy supply (t is time):

dedt∝f3.a2.m

The rate of energy supply per gram of mix is therefore given by:

dedt⋅1m∝f3.a2

The majority of this energy will appear as heat. If then we assume that there are no losses and that the rates of the amalgamation reactions obey an Arrhenius-type model for their temperature dependence (since they depend primarily on diffusion) (cf. equation 3§3.3), the relative rate factor ρ will be dependent on the temperature:

ρ≈e‐1/T≈T

for modest temperature rises from around 300 K. The temperature rise would be given by:

ΔT∝dedt⋅1m⋅tcp

where c_p is the specific heat capacity (J/K/g). Since the relative rate factor may be taken as 1 at room temperature, it is therefore about (f ³.a²) times greater at the end of the mixing process. However, we need the average relative rate factor for the mixing time to determine the overall effect. The geometric mean is appropriate to an exponential function; the average relative rate factor < ρ > will then be:

<ρ>∝1×f3.α2=f1.5.α

Hence the actual overall rate of amalgamation will be given by (2.4) × (2.7):

<ρ>⋅dedt⋅1m∝f4.5.a3

Now the progress of amalgamation is observable because the mix changes steadily in appearance from a powder to a single pellet (Fig. 2.1).^[2] This latter stage is very easily identifiable. We define the time taken for it to appear as the coherence time, t_c. This being a time, it is inversely proportional to the rate (s^– 1) for the process, so at constant mass:

tc−1∝f4.5.α3

This shows the quite unexpected sensitivity of the rate on two design aspects of the machine: its frequency of oscillation, and the amplitude of that movement (the distance between the extremes of motion of, say, the centre point of the capsule). It does, however, confirm the general assumption that increasing the speed of the machine is beneficial. It follows also that, for consistency in operation, the electric motor of an amalgamator must have a very stable running speed, unaffected by changes in supply voltage, temperature, load, or age. Equally, the amplitude of the oscillation must be stable – meaning that the springs do not soften or spread with use. The high powers in relation 2.8 indicate high sensitivity to small changes.

•2.1 Power rating

Several other things emerge from this analysis. Firstly, the design of the mixing machine is characterized by relation 2.4. From this we can define a Power Rating, PR, for the machine:

PR=f3.a2

with the units of W/kg (see box) or, equivalently, mW/g, to put it on a more relevant scale. That is, the maximum power available for the mixing process is proportional to this value, independently of all other factors. PR is therefore an objective measure of the capability of mixing machines. Whether this capability is usable is a matter to be determined.

•2.2 Heating

Secondly, relations 2.4 and 2.6 show that:

ΔT.s‐1∝f3.a2

which implies that the rate of temperature rise is dependent only on the PR of the machine (apart from some efficiency factor hidden in the constant of proportionality). In other words, the mass of the mix is quite irrelevant since this only controls the rate of energy delivery, and the specific heat capacity (J/K/g) from mix to mix will be essentially constant. To put it another way, every mix of amalgam must get warm as a necessary consequence of being mixed. The warmth of the pellet when it emerges from the capsule cannot be used to judge whether the amalgam has been overmixed or not, as is sometimes suggested. ‘Overheating’ of mixes has been blamed for various faults from time to time, but clearly this heating effect cannot be avoided, unless the mixing rate is low enough that heat can be conducted away; meanwhile, setting reactions continue.

•2.3 Performance

Now whether or not the above analysis is sufficiently representative of the true state of affairs can be tested, since the formation of the single pellet is so clearly-defined as a stage in the mixing process. After this pellet has formed, so long as it stays plastic, the energy calculations will be similar but there is no longer any easily monitored attribute of the mix to use to follow the changes. If the pellet hardens, and the collisions become more elastic, the physics may be different and the calculations much more difficult. However, all of the factors which may reasonably be expected to control the efficiency of mixing, such as alloy particle size, shape, cleanliness and reactivity; capsule size, shape and wall friction; alloy : mercury ratio; mass of mix; and mixing machine details such as capsule path and the velocity profile along that path, can all be taken into account by one measurement of the coherence time. This therefore is a performance measure for the entire alloy-capsule-machine system.

Experimentally, the effect of variation in frequency and amplitude on coherence time is shown in Fig. 2.2. Although some deviations from the theoretical slope of -4·5 do occur at high frequency and high amplitude, the analysis above is seen to be satisfactory over a substantial region. The complete failure below a certain frequency on curves a and b (the vertical portions of the plots) illustrates the need for a minimum impact energy for amalgamation to occur, corresponding to an activation energy. If the impact is too gentle, abrasion of the oxide will not occur.

The effect of variation in the mass of the mix is also found to be broadly as predicted from relation 2.8, i.e.:

rate∝f4.5.α3.m∝tc−1

(Fig. 2.3). Strangely, this contradicts the advice usually to be found with amalgam products that the larger doses (double ‘spill’ capsules) require longer mixing time. There is no physical basis for this advice, and no experimental evidence that it is necessary.

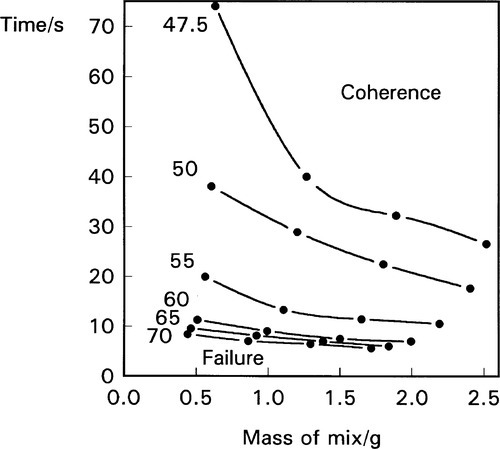
Figure 2.3 also shows that mixing to coherence occurs faster the more mercury is present, but that there is always a mercury content below which coherence will not be attained, no matter how high the machine’s PR. This of course has more to do with the mechanics of the pellet than the reaction with mercury and so must be product-dependent. With little liquid the pellet will be very porous and so very weak; impact will fracture it rather than cause consolidation. More importantly, Fig. 2.3 also shows that the mercury : alloy ratio can have a marked effect on the mixing rate, particularly at the lower ratios appropriate to modern alloys and techniques. This means that, for consistent results, the proportioning must be done accurately, when this in done in the clinic for reusable capsules. Furthermore, it sets limits on the acceptable variation in dosing or, perhaps more significantly, the completeness of delivery of the mercury from its reservoir, in preproportioned (disposable) capsules. Many such products are found to have crevices or other features that trap part of the mercury, in a poorly reproducible fashion, and much apparent inconsistency in the behaviour of the mixture can be traced to this – on top of the actual variation in both alloy and mercury actually put into the capsule.

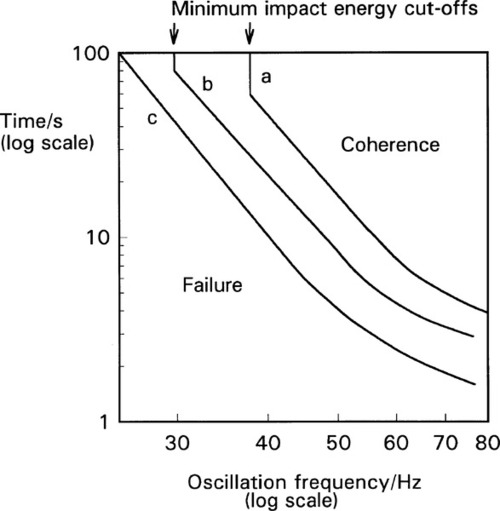
•2.4 Capsule

The capsule itself is an important component of the system and must be considered as part of the machine.^[3] The crucial factor is the ratio of the internal length of the capsule to the amplitude (as defined above): the length : amplitude ratio (L/a). Because it is an oscillating system an harmonic analysis is appropriate. However, there are so many extra factors controlling the efficiency of mixing that this becomes impractical. Capsule geometry and both oscillation path and waveform are quite variable between brands, and the detail of their effects and interactions not well known. Hence a direct experimental determination of the combined effect of these factors is more effective (Fig. 2.4), and in the long run much more meaningful as a direct statement of performance. The optimum L/a value can be seen to be only broadly defined (which is fortunate as this gives some freedom of design), but very clearly the worst efficiency occurs for L/a ≥ π/2, that is ≥ ~ 1·6, even at large amplitude (curve c). It is quite simply impossible for amalgam to be mixed in some capsules on some machines – nothing happens (curves a, b). It is important to appreciate that this failure to mix has no direct bearing on the quality of an amalgam product or of a machine as such, they can be entirely satisfactory otherwise. It simply indicates a mismatch of parameters – an unserviceable combination. As can be seen from the figure, very short coherence times can be obtained by a suitable choice of capsule and machine. Most commercial machines have amplitudes of the order of 15 ~ 18 mm.

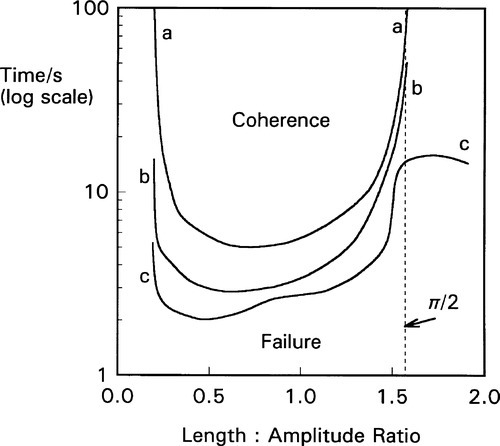
This behaviour can in part be understood by considering the impacts of the mixture with the capsule end. Unless the capsule motion takes the one end past the centre, overtaking the mixture, there will be no impact and it will not be accelerated. In other words, a long capsule can oscillate ar/>