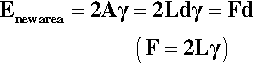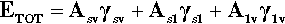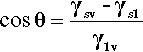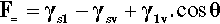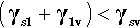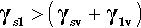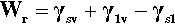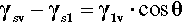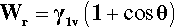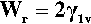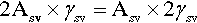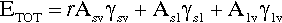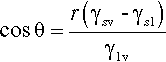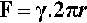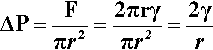It has been suggested that dentistry is very largely concerned with interfaces: the adhesion of plaque, the retention of full dentures, the cementation of devices, the application of fissure sealants and fluoride treatments, and so on; all depend on the properties and behaviour of tissue and other surfaces. Thus, in order to understand the effects and processes of dental procedures and treatments, their successes and failures, it is necessary to consider surface chemistry and physics. This will then guide the selection of designs and treatments in many contexts.

§1 Wetting

Whilst restorative dentistry is needed (which will be so long as tooth tissue continues to be lost through caries or trauma), the repair of developmental defects is attempted, or even cosmetic changes are desired by the patient, the retention of the restoration is of central interest. Hence, the search for direct restorative or cementation materials that are truly adhesive in dentistry is based on ideas such as the desirability of restorations being permanent, or at least as long-lived as possible, and orthodontic appliances being firmly held for as long as is required. This begs the question of what actually constitutes adhesion. In the circumstances, it is probably better to drop the use of the word adhesion, at least for the time being, and instead to discuss the nature of the bond between two substances. The use of the term ‘specific adhesion’ has been used to emphasize the difference between purely mechanical and purely chemical effects. But apart from the gross mechanical retention afforded by dovetail joints and similar undercuts in restorations, as exemplified by amalgam or a partial denture framework utilizing clasps, it is not really that clear-cut a distinction in practical dentistry. The reason for this is that to obtain mechanical interlocking of the surface roughness of tooth tissue on a microscopic scale, whether or not etched by, say, a resin-based restorative material, the wetting of the one by the other is an essential prerequisite.

•1.1 Contact angle

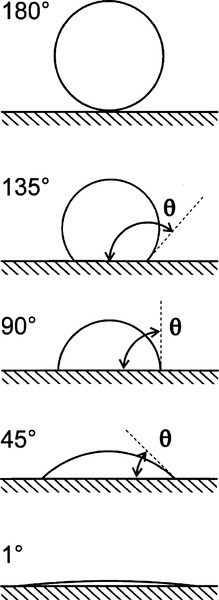
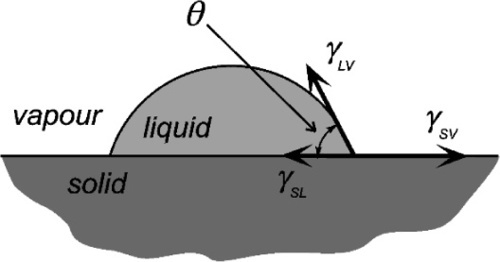
The fundamental effect of interest is the degree or ease of wetting, and this is conveniently studied through measurements of the contact angle exhibited by the fluid material on the substrate (Fig. 1.1). This is defined as the angle included between a plane tangent to the surface of the liquid and a plane tangent to the surface of the solid, both being at a point on their line of contact,measured through the liquid. It can be seen that liquid drops may exhibit a variety of extents of spreading on a surface (see, for example, water on wax or alcohol on glass). The greater the tendency of the liquid to wet and spread, the smaller the contact angle, until it vanishes when perfect spreading is observed. It is now necessary to explain how this comes about, and what the physical driving forces are that underlie this behaviour.

It has already been said that in order to fracture a solid material work is done in creating the two new surfaces (1§7): there is a characteristic amount of energy required per unit of area of new surface, and this is called the surface energy, γ (J/m²). This is no less true for liquids. A raindrop in free fall always tends to assume a perfectly spherical shape, as this is the one unconstrained surface that minimizes the surface area, and hence the total surface energy, for a given volume. Any system will, of course, tend towards a state of minimum total energy: this is a thermodynamic requirement. Because the water is fluid, and the droplet can therefore change shape, a mechanism exists for this minimization to occur. Thus, work has to be done on the raindrop by the friction of the air in falling to disturb it from its spherical shape. Likewise, droplets of one liquid in another, such as an emulsion (8§4.1), tend to become spherical – viscosity and time permitting.

•1.2 Surface tension

One physical interpretation of this tendency of liquids to change their shape spontaneously after a disturbance is the concept of surface tension (Fig. 1.2) where the apparent surface skin of the liquid is attributed to the difference in the number of molecules mutually attracted by molecules at different positions. Simplistically, this mutual attraction of molecules explains the tendency to minimize surface area because this also minimizes the number of ‘unbalanced’ molecules at the surface.

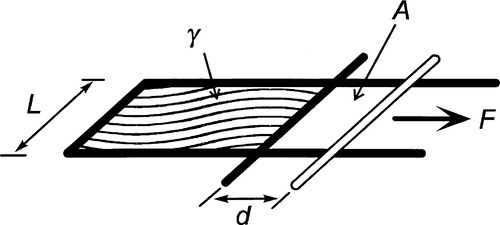
Surface tension, also given the symbol γ, is expressed as a force per unit length (N/m) (that is, a line stress), but since a joule is defined as 1 N.m (force × distance acted over), surface energy and surface tension can be seen to be entirely equivalent: J/m² = N.m/m². It is just the conceptual approach that differs, one’s point of view, so to speak. (Note that the surface energy here is understood to be specific rather than total.) Hence, the work done in extending a surface, counting both sides of the film (Fig. 1.3), is identical to the work done creating the same area by splitting a column of liquid (Fig. 1.4), again counting both new surfaces:

< ?xml:namespace prefix = "mml" ns = "http://www.w3.org/1998/Math/MathML" />Enewarea=2Aγ=2Ldγ=FdF=2Lγ

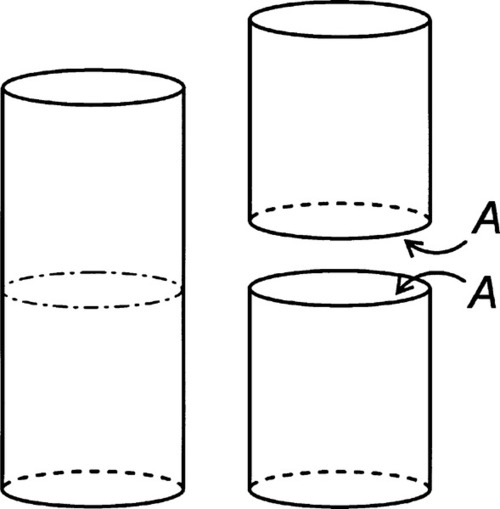
Surface tension may be measured directly as the force required to extend a film (Fig. 1.3) but more usually by a method equivalent to that shown in Fig. 1.5, i.e. by pulling on an object attached to a liquid surface and measuring the force required.

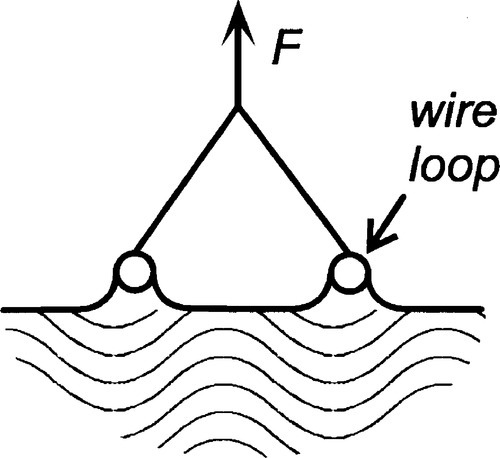
•1.3 Interfacial energy

So far we have discussed the fluid as if it were in vacuum, unaffected by any gas molecules above its surface. Indeed, when we consider the surface energy of a solid, we take it for granted that we are working in air at ‘normal’ temperature and pressure. Solids usually have entirely negligible vapour pressures (iodine is a notable exception, 0.31 mm Hg at 25 °C), so the composition of the air is unaffected. This is not, in general, the case with liquids. They will be more or less volatile, having appreciable vapour pressures, so that the ‘air’ must have some proportion of the vapour present. But the attraction from molecules in any vapour from the liquid tends to balance the forces acting on surface molecules of the liquid from within it. This is why we must refer to such systems at equilibrium, i.e. with saturated vapour, if any measurements are to be meaningfully reproducible.

In other words, if γ_s is the surface tension of the solid against a vacuum, and γ_sv is the value equilibrated against some vapour, γ_s > γ_sv then. There are in fact adsorbed molecules on that surface, although not necessarily a full layer, and the extra energy for the surface against a vacuum can be explained as the work required to remove those adsorbed molecules.

In fact, the mere existence of a liquid surface depends on the attractive forces operating between the dense liquid and its much less dense vapour, and indeed any other gas molecules present, this force being less in total magnitude than between the molecules of the liquid. The implications of this may perhaps be seen when a liquid substance is raised above the critical temperature (at the critical pressure): the otherwise clear boundary between liquid and vapour simply ceases to exist as the densities of the two phases become indistinguishable. Because there is no surface, there is then no surface tension. It has in fact diminished steadily to zero as the temperature is raised

Similarly, any other liquid in contact with the first will have its own cohesive forces acting, and there will also be some interaction between the molecules of the two liquids. Since the second liquid will usually be very much denser (more compact) than the vapour of the first (i.e. the molecules more numerous per unit volume), even quite weak interaction between the two liquids leads to a generally lower interfacial energy, as it is now called, than either of the individual liquids’ surface energies when in contact with their vapours.

•1.4 Energy minimization

So it is with a liquid on a solid: very often there will be a lower interfacial energy between the liquid and the solid than between the liquid and its vapour. There is then a tendency for the liquid to spread on the solid – which is energetically favourable. However, this spread necessarily implies a change in the surface area of the liquid against the vapour – which needs to be allowed for because the total liquid-vapour surface energy there is changed. There is also the decrease in the area of the solid against the vapour of the liquid to take into account.

We shall consider the simple case of a liquid drop on a plane, uniform¹, homogeneous², rigid, isotropic³ solid surface, but the results are extendable (with some effort) to other conditions. We know first that the shape of the liquid-vapour interface must be a spherical cap (Fig. 1.6) because, for any given liquid–solid interfacial area, this is the shape that minimizes that surface. We derive this as follows: a sphere is the closed surface of minimum area. The two parts cut off by an intersecting plane must also each be of a minimum area for the fixed intersection line since if either were not it implies that their sum, the original spherical surface, was not at a minimum in the first place. It follows then that the liquid–solid interface is a circular disc, since any section through a sphere gives a circle.

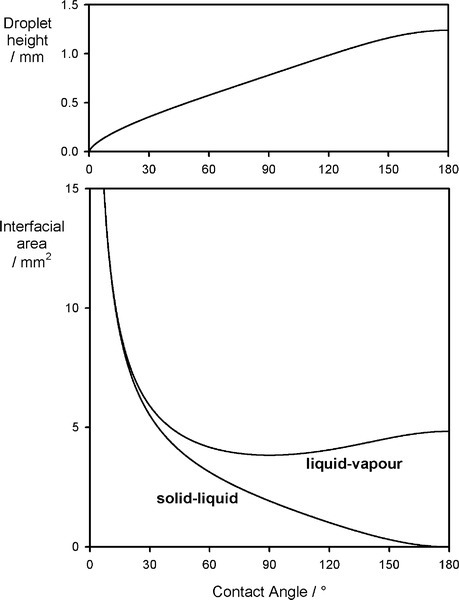
A sense of the nature of the variations in the interfacial areas as a drop spreads can be gained from Fig. 1.7. In order to understand this and its consequences, an equation for the total energy, E_TOT, of the system must be written. This takes the form of the sum of the product of the surface area A of an interface with its specific surface energy, γ for each of the interfaces present:

ETOT=Asvγsv+As1γs1+A1vγ1v

where the subscripts s, l and v refer to solid, liquid and vapour respectively and the pairs identify the interface in question. It is this sum that must be minimized for thermodynamic equilibrium.

By the application of a little geometry, it can be shown that the minimum in equation 1.2 is obtained for the spherical cap whose contact angle θ is obtained from

cosθ=γsv‐γs1γ1v

This is called the Young equation. This result is on the assumption that the solid surface is ideal in the sense that the surface energy is constant from point to point. Even if it were not, the thermodynamic minimization must still occur, but the geometry becomes much more complicated and our ability to calculate a solution is somewhat impaired. Gravity, too, is ignored in equation 1.3, but for small drops the flattening that this causes, due to hydrostatic head, can safely be ignored. In addition, it is assumed that viscosity does not play a role, and that dissolution of the substrate – and of the liquid in the substrate – can be ignored. That is, all kinetic aspects have been allowed to equilibrate or are negligible. Despite all this, the general principle of the minimization of the total energy still stands as the driving force for the adjustments in shape that are observed when any liquid drop is placed on any surface. Systems of relevance to dentistry include fissure sealants into crevices, mercury on silver amalgam alloy, investment slurry on wax, and so on.

It is possible to deduce from equation 1.3 what conditions are required to promote wetting or non-wetting depending on the application and the intention. Low surface tension liquids clearly will wet more effectively, and particularly if they are on high energy solid surfaces, aided by a strong interaction between the liquid and the solid to lower that interfacial energy. Conversely, low surface energy solids (such as polytetrafluoroethylene, ‘ptfe’ or ‘Teflon’) will be difficult to wet, and high surface tension liquids, such as mercury, do not wet most surfaces, and in particular not ceramics.

•1.5 Force balance

Given that we found an equivalence between surface energy and surface tension above, there is an alternative approach to the solution of this problem based on the surface tensions which are operating.

In any given surface (at equilibrium), the surface tension acting on one side of an arbitrary line drawn on that surface must be exactly balanced by the identical tension on the other side. But if a drop of liquid is placed on a surface a line is established that disrupts that balance. The contact line or three-phase line (the ‘TPL’) is the boundary line along which solid, liquid and vapour meet simultaneously. Consider, for example, the view from the solid: the solid-vapour interface no longer exists on one side of that line, and it is replaced there by a solid-liquid interface whose interfacial tension is in general different from that of the solid-vapour interface. Across that contact line is therefore an imbalance. Equally, from the point of view of the liquid, part of the liquid-vapour interface has been replaced by that of the solid-liquid. There is again an imbalance of tensions across the contact line, but this time generally at some arbitrary angle. Because of these unbalanced forces acting on the line, the line must move, and it will move until the resultant of all three forces, F₌, is precisely zero in the plane of the solid surface at the contact line. This force-vector approach (Fig. 1.8) leads to the following straightforward equation being written down directly:

F==γs1−γsv+γ1v.cosθ

each term having a magnitude and a direction. This can be seen to be only a rearranged version of equation 1.3, and thus equally well expresses the thermodynamic result at equilibrium.^[1]

It should be clear from this that contact angle is not, in fact, just a property of the liquid itself at all, but a geometrical consequence of the particular values that the three interfacial energies have for a given system (and these, of course, vary with temperature). In other words, it is not a physical constant but a behaviour dependent on all local circumstances that influence any element of the system. Again, it is a property of the combination of the particular solid, liquid and gas phases – composition, constitution and structure, as appropriate.

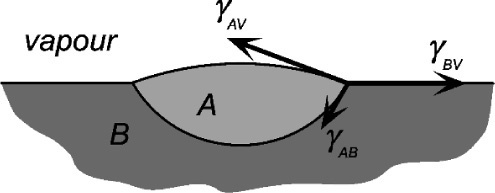
In Fig. 1.8 it might be noticed that there is an additional force component, normal to the surface, of (γ_1v.sin θ, that is left apparently unbalanced. To see why the complementary downward force does not appear in equation 1.4, consider the situation of a drop of a liquid A floating on immiscible liquid B (Fig. 1.9). Here there are again three interfaces to consider, but the force balance is complete because of the deformation of the surface of liquid B. Liquid A has two spherical section surfaces of different radii of curvature. In other words, in Fig. 1.8, the solid surface cannot deform (measurably), so the downward balancing force of –γ_lv.sin θ has no bearing on the calculation: the three-phase line can only slide in the plane of the solid surface. The normal forces still exist, but are accounted for by equilibrium elastic deformation of the solid (but which is usually far too small to be of any importance).

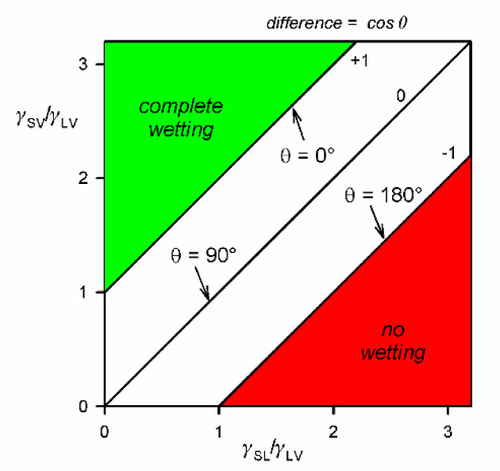
Consideration of equation 1.4 will show that there are circumstances when no real value of θ can cause the sum to be zero. Thus, if

γs1+γ1v<γsv

then F₌ is negative (limiting cos θ = + 1), which means a net tension pulling the contact line over the unwetted solid surface. This corresponds to perfect wetting and is accompanied by spontaneous spreading, the limit presumably being a monomolecular film.

On the other hand, if

γs1>γsv+γ1v

then F₌ is positive (limiting cos θ = − 1), and the contact line would be driven to retreat across any already wetted surface until the contact area, the solid-liquid interface, vanishes.

These conclusions can also be seen in the equivalentequation 1.3 where quite clearly it is very easily possible to construct ratios whose values lie outside of the range [- 1,+1]. This is not an indication of the failure of the theory, but rather an illustration of the fact that the intermediate condition of partial wetting, – 1 ≤ cos θ ≤ + 1, is a rather special occurrence (Fig. 1.10). This observation reinforces the remark above that contact angle is not in any way a property of the liquid but a characteristic of the system as a whole.

•1.6 Critical surface tension

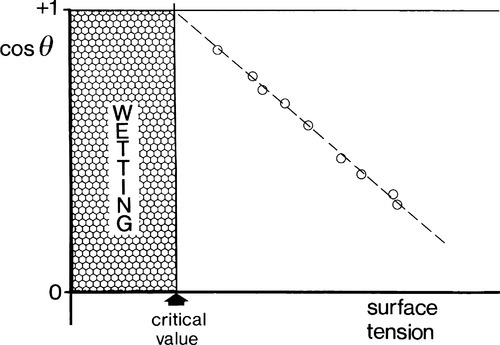
There are considerable difficulties with measuring individual solid interfacial tensions, and it is certainly easier to measure contact angles. But, in the region of perhaps most interest, θ approaching 0°, the determination of angles is difficult and an indirect approach is sometimes of value. For a given substrate, θ is measured for a series of homologous liquids (the aliphatic alcohols for example, or the paraffins themselves). The surface tensions of the liquids are independently measurable by other means (Fig. 1.5), and cos θ is then plotted against γ_lv (Fig. 1.11). This is known as a Zisman plot. The plotted points tend to fall on a straight line and an extrapolation can be made to estimate the critical surface tension, the value above which full wetting will not occur, and below which spontaneous spreading will be observed – for that substrate. Necessarily, this approach has to be used with caution because the result only applies to a similar liquid, one whose chemical interaction with the substrate is similar to that of the others of the test series.

•1.7 Work of adhesion

The necessity of counting both new surfaces in crack formation, film extension and so on can be demonstrated using the above results. The reversible work of adhesion, W_r, is the work required to separate the liquid from the solid, and is given by:

Wr=γsv+γ1v−γs1

(using the interchangeability of surface tension and surface energy). This equation is to be read as saying that for each unit of area of solid-liquid interface that is separated (i.e., removed), one unit of area of each of solid-vapour and liquid-vapour is created. Now, from equation 1.4,

γsv−γs1=γ1v⋅cosθ

Substitution from 1.8 in 1.7 gives:

Wr=γ1v1+cosθ

known as the Young-Dupré equation, which applies to any system where chemical changes do not occur on wetting. But if we imagine now that the same liquid is substituted for the solid substrate, we have of course θ = 0°, cos θ = + 1, so that

Wr=2γ1v

In other words, the work done on joining together two liquid surfaces is precisely twice the surface energy. This result necessarily applies by extension to solids also, and serves to illustrate the reason for existence of the work of fracture previously discussed.

•1.8 Boundary layer

Reference was made to the existence of a boundary layer on a filler and the effect that this has on viscosity (4§9.2). It is now possible to see that since wetting implies a lowered interfacial energy, the molecules forming that layer are by definition in a more stable position than those further away: they are adsorbed to the filler. They do not exchange with the bulk of the liquid so readily, and are more organized because they are constrained to be a two-dimensional entity, following the surface of the other phase. Indeed, depending on the strength of the binding to the substrate, the boundary layer may be described as a two-dimensional liquid or even partly crystal-like. The ordering this represents may therefore have an influence on the next nearest neighbours, and so on, so that the effective thickness of the boundary layer may be several molecules thick, depending on the strength of interactions between molecules. The hydrogen bonding of water is clearly important in this context, and comparison may be made with the template effect of polysaccharides (7§8.2). The variation in behaviour between fillers as to their effect on viscosity can therefore be seen to depend in part on the chemical nature of the surface as well as surface area and matrix chemistry.

•1.9 Roughness

The calculations above involving surface energy implicitly assume that the respective surfaces are smooth – perfect geometrical planes and spherical caps. In such cases the specific surface energy is appropriate because the actual area of the interface enclosed by the relevant boundaries is exactly the area of the ideal delineated shape. For liquids, this is perfectly acceptable. However, real solid surfaces are rough, having a true surface area perhaps as much as two or three times the apparent size. Clearly, it is the true area of interface that must be used in any calculation. It is obvious that doubling the area inside a perimeter is numerically the same as doubling the specific surface energy:

2Asv×γsv=Asv×2γsv

Thus, if the roughness factor, r, is given by:

r=actualareadelineatedarea

then equation 1.2 becomes

ETOT=rAsvγsv+As1γs1+A1vγ1v

such that equation 1.3 becomes:

cosθ=rγsv‐γs1γ1v

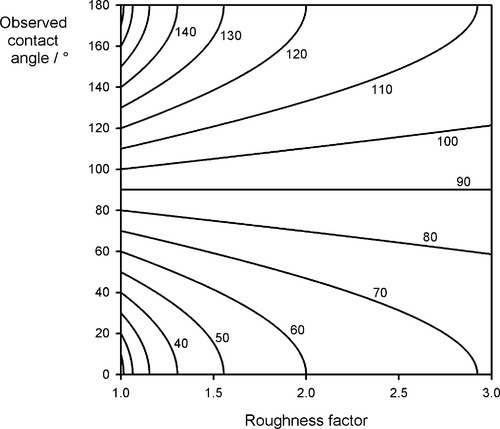
In other words, the effect of roughness is to magnify the effect of the gain or loss of energy occurring in replacing the sv interface with the sl: if this is favourable, it becomes more so; if not, it is made worse^[2]. The effect is illustrated in Fig. 1.12. For a ‘perfect’ contact angle of 90° (when r = 1), there is no change, but if there is any better wetting than this, a rough surface improves it, and this can be quite dramatic for even a modest value of roughness factor of 1.5, where complete wetting (and thus spreading) is observed for a basic contact angle of about 47°. Conversely, droplets would roll cleanly off a surface with r = 2 for θ = 120°. It is a combination of microscopic texture and the waxy surface of many leaves that allows rain drops to be shed from them so easily.

•1.10 Levelling

One manifestation of the spontaneous tendency to minimize the surface area of a liquid is self-levelling. That is, a rough or wavy surface will become smooth, even in the absence of gravity effects. This is seen very clearly in paint, where brushmarks tend to disappear while the paint is still fresh enough to be just viscous, and in flamed wax (16§2.6). The same thing drives the smoothing of a fractured glass surface at a high enough temperature, and can be seen to a lesser extent in freshly mixed dental cements, filled resins, and so on, depending on whether there is a yield point, time allowed, and the radius of curvature.

•1.11 Experimental considerations

It may seem that the experimental determination of contact angle is a straightforward matter, but a number of factors must be borne in mind for meaningful results. Firstly, it has been emphasized that the equilibrium state that is the goal has to be with respect to the vapour of the liquid. More specifically, it has to be the saturated vapour if the thermodynamic conditions are to be met. Failure to achieve this not only affects the interfacial energies concerned, but might lead to appreciable evaporation of the liquid. If this liquid is itself a solution, then its concentration must change, and with it the interfacial energies. Secondly, any dissolution of the substrate, or components of it, changes both liquid and solid, including the roughness of the latter (§1.9). Even slightly soluble substances could have significant effects. Thirdly, the liquid should not dissolve in the substrate, for example, water in polymers. Testing polymeric materials as used in the mouth implies that they are saturated with water. Each of these can give time-varying behaviour. In addition, the presence of surface-active substances in the solution, such as glycoproteins in saliva, means that the true substrate surface is coated and obscured such that what is tested is the chemisorbed (multi-molecular) layer instead. This is a quite different matter since this will tend to be chemically similar no matter what substrate is underlying.

§2 Capillarity

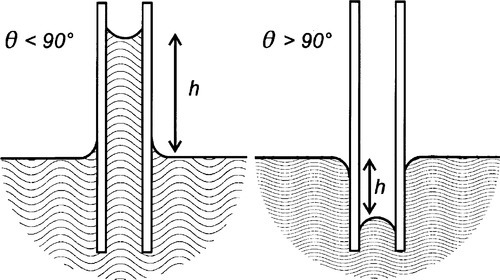
Surface tension has another important manifestation which has many implications in dentistry: that of capillary rise or capillarity (Fig. 2.1). The same forces that cause the boundary of the liquid to move on the solid when this is horizontal, adjusting the position of the contact line, may also be observed to operate on vertical surfaces. The lens-like surface of water in a glass tube (such as a burette) – the meniscus, and the curved edge around the liquid in a cup should be familiar phenomena. It is this curvature that causes capillary rise. However, to demonstrate this, another system must first be examined.

•2.1 Droplets and bubbles

Consider a spherical droplet of radius r (Fig. 2.2). For any line segment drawn on a liquid surface, the total force acting on it is given by the product of its length and the line stress due to the surface tension of the liquid. Thus, if the line is a meridian (i.e., a full circle from pole to pole) on a droplet, length 2πr, the total force F acting on it is given by

F=γ.2πr

(We can drop the subscripts ‘lv’ when this interface is understood.) This generated force is acting in the sense of minimizing the area overall, and thus can be seen to be squeezing the contents of the droplet. It must therefore act over the entire cross-section (area = πr²), so the increase in pressure ,∆P, inside the drop with respect to the outside is given by:

ΔP=Fπr2=2πrγπr2=2γr

which is known as the Laplace equation.

For a droplet, the pressure is positive (compressive) in the liquid, and this is taken to define the curvature, C = 1/r, of the drop’s surface to be positive (Fig. 2.3, left). This point is important because it establishes the sense of the pressure difference in any system. Thus, in a bubble of gas in a liquid, which can be represented by the same diagram, Fig. 2.2, the pressure in the gas of the bubble is higher than the pressure in the liquid by the amount given by equation 2.2. From the point of view of the liquid, the curvature of the interface is negative (curving away from the observer), so the pressure in the liquid is relatively negative with respect to the gas. We could change the viewpoint, and just as accurately say that from the point of view of the gas the surface curvature is positive (wrapping around the observer), and that therefore the pressure in the gas is higher than that in the liquid (Fig. 2.3, right).

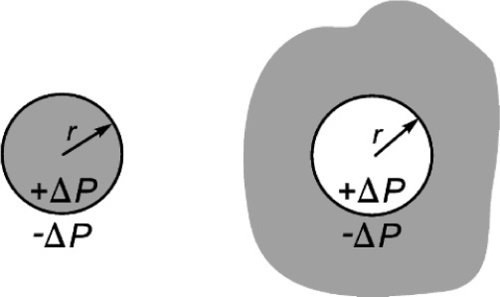
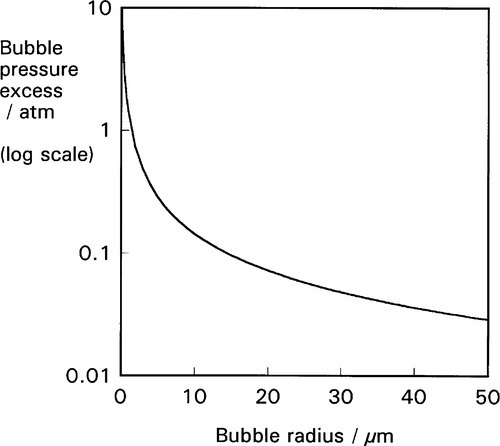
This effect is not insignificant: very small bubbles will have very high pressures (Fig. 2.4). Put simply, it is merely the curvature of the boundary that generates the pressure difference across the interface. In other words, it is of no consequence what lies either side of the boundary, the physical effect and its sign is the same. It is only the magnitude of the effect that depends on the surface energy of that interface.

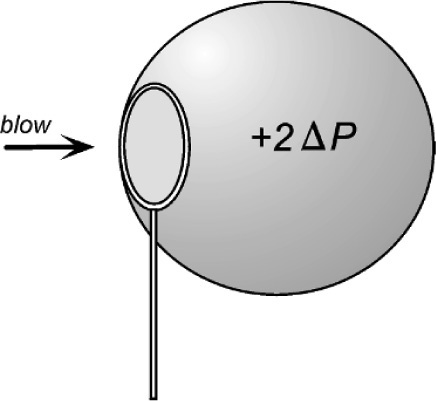
In passing, we can observe that a soap bubble has two boundary surfaces, an inner and an outer, either side of the liquid soap solution. There are therefore two contributions to the excess pressure inside the bubble, which is very nearly double that of the single surface value because the two radii are very similar, since the soap film is thin. Of course, the mere fact that a bubble has to be blown (Fig. 2.5) shows that a pressure difference is involved.

In deriving equation 1.3 we noted that a spherical surface has minimum area and therefore minimum energy. We can obtain a further view of what this means by considering the curvature. If the curvature of the surface of an unconstrained droplet or bubble varied from point to point across the surface, that/>